前言
写在前面
因为编程底子差,加之数值分析虽然上课还比较认真,吧(至少在大力老师面前我还是一个乖孩子)。最不能接受的就是课程设计当理论报告写去了,所以索性把数值分析这本书重学了!!
重学的原因有几点:
-
这是一本友善的英文书籍,虽然大创看过很多英文论文,但是多半是强大的DeepL翻译软件帮我克服语言障碍
-
未来我需要使用**《机器学习》**里面的东西,大量依赖数值分析的基本方法!什么最速梯度下降啊啥的,太吃数值分析了!!
-
因为报告是水过去的嘛(bushi),所以写一点忏悔一点
所以下面开始了!!
单变量方程的解
二分法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| function zero_point = Bisection(F, endpoint_a, endpoint_b, TOL, N)
if F(endpoint_a) * F(endpoint_b) < 0
i = 0;
FA = F(endpoint_a);
while i < N
p = (endpoint_a + endpoint_b) / 2;
FP = F(p);
if FP == 0 || p - endpoint_a < TOL
zero_point = p;
break;
else
i = i + 1;
if FA * FP > 0
endpoint_a = p;
else
endpoint_b = p;
end
end
fprintf("第%d次迭代区间为:[ %f , %f ]\n", i, endpoint_a, endpoint_b);
end
else
disp('无法判断是否存在零点');
end
end
|
例如:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| >> F = @(x)log(x) - x^0.5 + x - 3
>> Bisection(F, 1, 10, 0.00001, 100000)
第1次迭代区间为:[ 1.000000 , 5.500000 ]
第2次迭代区间为:[ 3.250000 , 5.500000 ]
第3次迭代区间为:[ 3.250000 , 4.375000 ]
第4次迭代区间为:[ 3.250000 , 3.812500 ]
第5次迭代区间为:[ 3.531250 , 3.812500 ]
第6次迭代区间为:[ 3.531250 , 3.671875 ]
第7次迭代区间为:[ 3.601563 , 3.671875 ]
第8次迭代区间为:[ 3.601563 , 3.636719 ]
第9次迭代区间为:[ 3.601563 , 3.619141 ]
第10次迭代区间为:[ 3.610352 , 3.619141 ]
第11次迭代区间为:[ 3.614746 , 3.619141 ]
第12次迭代区间为:[ 3.614746 , 3.616943 ]
第13次迭代区间为:[ 3.615845 , 3.616943 ]
第14次迭代区间为:[ 3.615845 , 3.616394 ]
第15次迭代区间为:[ 3.616119 , 3.616394 ]
第16次迭代区间为:[ 3.616119 , 3.616257 ]
第17次迭代区间为:[ 3.616188 , 3.616257 ]
第18次迭代区间为:[ 3.616188 , 3.616222 ]
第19次迭代区间为:[ 3.616205 , 3.616222 ]
ans =
3.6162
|
定点迭代法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| function zero_point = Fixed_Point(g, p_0, TOL, N)
i = 1;
while i < N
p = g(p_0);
fprintf('第%d次迭代结果为:%f\n', i, p);
if abs(p - p_0) < TOL
zero_point = p;
break;
else
i = i + 1;
p_0 = p;
end
end
if i >= N
disp('超出最大迭代次数,无法判断零点')
end
end
|
例如:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| >> g = @(x) 0.5 * (10 - x^3)^0.5
>> Fixed_Point(g, 1.5, 0.0001, 100000)
第1次迭代结果为:1.286954
第2次迭代结果为:1.402541
第3次迭代结果为:1.345458
第4次迭代结果为:1.375170
第5次迭代结果为:1.360094
第6次迭代结果为:1.367847
第7次迭代结果为:1.363887
第8次迭代结果为:1.365917
第9次迭代结果为:1.364878
第10次迭代结果为:1.365410
第11次迭代结果为:1.365138
第12次迭代结果为:1.365277
第13次迭代结果为:1.365206
ans =
1.3652
|
牛顿法及其拓展
牛顿迭代法
pn=pn−1−f′(pn−1)f(pn−1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| function zero_point = Newton(F, p_0, TOL, N)
i = 1;
f = sym(F);
df = diff(f);
dF = matlabFunction(df);
while i < N
p = p_0 - F(p_0) / dF(p_0);
fprintf('第%d次迭代结果为:%f\n', i, p);
if abs(p - p_0) < TOL
zero_point = p;
break;
else
i = i + 1;
p_0 = p;
end
end
if i >= N
disp('超出最大迭代次数,无法判断零点')
end
end
|
例如:
1
2
3
4
5
6
7
8
9
10
11
12
| >> F = @(x)log(x) - x^0.5 + x - 3
>> Newton(F, 1, 0.00001, 100000)
第1次迭代结果为:3.000000
第2次迭代结果为:3.606360
第3次迭代结果为:3.616205
第4次迭代结果为:3.616207
ans =
3.6162
|
割线法
pn=pn−1−f(pn−1)−f(pn−2)f(pn−1)(pn−1−pn−2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| function zero_point = Secant(F, p_0, p_1, TOL, N)
i = 2;
q_0 = F(p_0);
q_1 = F(p_1);
while i < N
p = p_1 - q_1 * (p_1 - p_0) / (q_1 - q_0);
fprintf('第%d次迭代结果为:%f\n', i - 1, p);
if abs(p - p_1) < TOL
zero_point = p;
break;
else
i = i + 1;
p_0 = p_1;
q_0 = q_1;
p_1 = p;
q_1 = F(p);
end
end
if i >= N
disp('fail')
end
end
|
例如:
1
2
3
4
5
6
7
8
9
10
11
12
13
| >> F = @(x)log(x) - x^0.5 + x - 3
>> Secant(F, 1, 10, 0.00001, 100000)
第1次迭代结果为:3.953949
第2次迭代结果为:3.599312
第3次迭代结果为:3.616313
第4次迭代结果为:3.616207
第5次迭代结果为:3.616207
ans =
3.6162
|
试位法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| function zero_point = False_Position(F, p_0, p_1, TOL, N)
i = 2;
q_0 = F(p_0);
q_1 = F(p_1);
while i < N
fprintf("第%d次迭代后,根所在的区间为:[ %f , %f ]\n", i - 1, p_0, p_1);
p = p_1 - q_1 * (p_1 - p_0) / (q_1 - q_0);
if abs(p - p_1) < TOL
zero_point = p;
break;
else
i = i + 1;
q = F(p);
if q_0 * q < 0
p_0 = p;
p_1 = p_1;
q_0 = q;
q_1 = q_1;
else
p_0 = p_0;
p_1 = p;
q_0 = q_0;
q_1 = q_1;
end
end
end
if i >= N
disp('fail')
end
end
|
例如:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| >> F = @(x)log(x) - x^0.5 + x - 3
>> False_Position(F, 1, 10, 0.00001, 100000)
第1次迭代后,根所在的区间为:[ 1.000000 , 10.000000 ]
第2次迭代后,根所在的区间为:[ 3.953949 , 10.000000 ]
第3次迭代后,根所在的区间为:[ 3.599312 , 10.000000 ]
第4次迭代后,根所在的区间为:[ 3.617119 , 10.000000 ]
第5次迭代后,根所在的区间为:[ 3.616158 , 10.000000 ]
第6次迭代后,根所在的区间为:[ 3.616210 , 10.000000 ]
第7次迭代后,根所在的区间为:[ 3.616207 , 10.000000 ]
第8次迭代后,根所在的区间为:[ 3.616207 , 10.000000 ]
第9次迭代后,根所在的区间为:[ 3.616207 , 10.000000 ]
第10次迭代后,根所在的区间为:[ 3.616207 , 10.000000 ]
第11次迭代后,根所在的区间为:[ 3.616207 , 10.000000 ]
第12次迭代后,根所在的区间为:[ 3.616207 , 10.000000 ]
第13次迭代后,根所在的区间为:[ 3.616207 , 10.000000 ]
第14次迭代后,根所在的区间为:[ 3.616207 , 10.000000 ]
第15次迭代后,根所在的区间为:[ 3.616207 , 3.616207 ]
ans =
3.6162
|
重根问题
pn=pn−1−[f′(pn)]2−f(pn)f′′(pn)f(pn)f′(pn)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| function zero_point = Modified_Newton(F, p_0, TOL, N)
i = 1;
f = sym(F);
df = diff(f);
ddf = diff(df);
dF = matlabFunction(df);
ddF = matlabFunction(ddf);
while i < N
p = p_0 - F(p_0) * dF(p_0) / dF(p_0)^2 - F(p_0) * ddF(p_0);
fprintf('第%d次迭代结果为:%f\n', i, p);
if abs(p - p_0) < TOL
zero_point = p;
break;
else
i = i + 1;
p_0 = p;
end
end
if i >= N
disp('超出最大迭代次数,无法判断零点')
end
end
|
例如:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| >> F = @(x) exp(x) - x - 1
>> Modified_Newton(F, 10, 0.0000001, 10000000)
第1次迭代结果为:-484922895.285593
第2次迭代结果为:-1.000000
第3次迭代结果为:-0.553359
第4次迭代结果为:-0.325108
第5次迭代结果为:-0.188120
第6次迭代结果为:-0.104895
第7次迭代结果为:-0.056316
第8次迭代结果为:-0.029365
第9次迭代结果为:-0.015025
第10次迭代结果为:-0.007604
第11次迭代结果为:-0.003826
第12次迭代结果为:-0.001919
第13次迭代结果为:-0.000961
第14次迭代结果为:-0.000481
第15次迭代结果为:-0.000241
第16次迭代结果为:-0.000120
第17次迭代结果为:-0.000060
第18次迭代结果为:-0.000030
第19次迭代结果为:-0.000015
第20次迭代结果为:-0.000008
第21次迭代结果为:-0.000004
第22次迭代结果为:-0.000002
第23次迭代结果为:-0.000001
第24次迭代结果为:-0.000000
第25次迭代结果为:-0.000000
第26次迭代结果为:-0.000000
第27次迭代结果为:-0.000000
ans =
-5.8954e-08
|
加速收敛法
Steffensen法
Δpn=pn+1−pnΔkpn=Δ(Δk−1pn)pn=pn−1−Δ2pn(Δpn)2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| function zero_point = Steffensen(g, p_0, TOL, N)
i = 1;
while i < N
p_1 = g(p_0);
p_2 = g(p_1);
p = p_0 - (p_1 - p_0)^2 / (p_2 - 2 * p_1 + p_0);
fprintf('第%d次迭代结果为:%f\n', i, p);
if abs(p - p_0) < TOL
zero_point = p;
break;
else
i = i + 1;
p_0 = p;
end
end
if i >= N
disp('fail')
end
end
|
例如:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| >> g = @(x) 0.5 * (10 - x^3)^0.5
>> Steffensen(g, 1.5, 0.0001, 100000)
第1次迭代结果为:1.361886
第2次迭代结果为:1.365228
第3次迭代结果为:1.365230
ans =
1.3652
>> Fixed_Point(g, 1.5, 0.0001, 100000)
第1次迭代结果为:1.286954
第2次迭代结果为:1.402541
第3次迭代结果为:1.345458
第4次迭代结果为:1.375170
第5次迭代结果为:1.360094
第6次迭代结果为:1.367847
第7次迭代结果为:1.363887
第8次迭代结果为:1.365917
第9次迭代结果为:1.364878
第10次迭代结果为:1.365410
第11次迭代结果为:1.365138
第12次迭代结果为:1.365277
第13次迭代结果为:1.365206
ans =
1.3652
|
多项式的零点及Muller方法
Hoener
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| function [y, z] = Horner(n, aa, x_0)
disp('多项式为:')
poly2sym(fliplr(aa))
y = aa(n + 1);
z = aa(n + 1);
for j = n - 1:-1:1
y = x_0 * y + aa(j + 1);
z = x_0 * z + y;
end
y = x_0 * y + aa(1);
end
|
例如:
1
2
3
4
| >> aa = [-4, 3, -3, 0, 2]
>> [p, p_1] = Horner(4, aa, -2)
|
Muller
其实书上没讲多细,连证明收敛性都没有,讲真书上代码很牵强
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| function zero_point = Muller(F, p_0, p_1, p_2, TOL, N)
i = 3;
h1 = p_1 - p_0;
h2 = p_2 - p_1;
f1 = (F(p_1) - F(p_0)) / h1;
f2 = (F(p_2) - F(p_1)) / h2;
a = (f2 - f1) / (h2 + h1);
while i < N
b = f2 + h2 * a;
c = F(p_2);
delta = (b^2 - 4 * a * c)^0.5;
if abs(b - delta) < abs(b + delta)
e = b + delta;
else
e = b - delta;
end
h = -2 * c / e;
p = p_2 + h;
fprintf('第%d次迭代结果为:%f\n', i - 2, p);
if abs(h) < TOL
zero_point = p;
break;
end
p_0 = p_1;
p_1 = p_2;
p_2 = p;
h1 = p_1 - p_0;
h2 = p_2 - p_1;
f1 = (F(p_1) - F(p_0)) / h1;
f2 = (F(p_2) - F(p_1)) / h2;
a = (f2 - f1) / (h2 + h1);
i = i + 1;
end
if i >= N
disp('fail')
end
end
|
例如:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| >> F = @(x)x^4 - 3 * x^3 + x^2 + x + 1
>> Muller(F, 0.5, -0.5, 0, 0.00001, 100000)
第1次迭代结果为:-0.100000
第2次迭代结果为:-0.492146
第3次迭代结果为:-0.352226
第4次迭代结果为:-0.340229
第5次迭代结果为:-0.339095
第6次迭代结果为:-0.339093
第7次迭代结果为:-0.339093
ans =
-0.3391 - 0.4466i
|
插值多项式逼近
Lagrange插值法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| function P = Lagrange(F, xx, endpoint_a, endpoint_b)
syms x;
P = 0;
n = length(xx);
n = n - 1;
for k = 0:n
m = 1;
d = 1;
yy(k + 1) = F(xx(k + 1));
for i = 0:n
if i == k
continue;
end
m = m * (x - xx(i + 1));
d = d * (xx(k + 1) - xx(i + 1));
end
L = m / d;
P = P + L * yy(k + 1);
end
simplify(P)
p = matlabFunction(P);
fplot(F, [endpoint_a, endpoint_b]); hold on;
plot(xx, yy, '>'); hold on;
fplot(p, [endpoint_a, endpoint_b]);
end
|
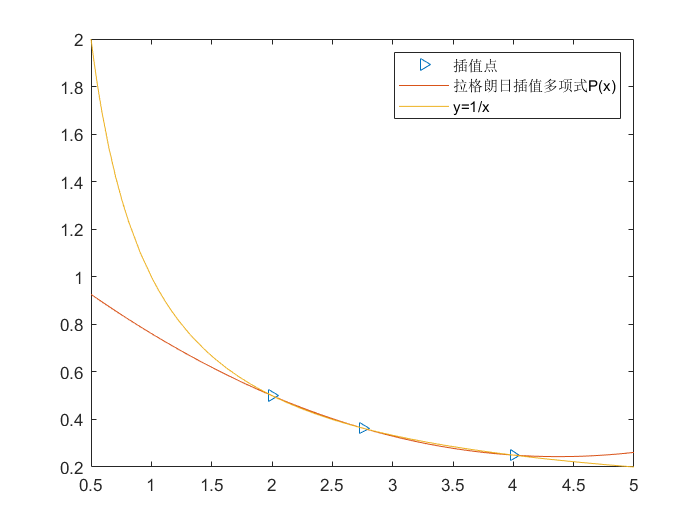
例如:
1
2
3
4
5
6
7
8
9
10
| >> xx = [2, 2.75, 4]
>> yy = 1 ./ xx
>> plot(xx, yy, '>')
>> hold on
>> P = Lagrange(xx, yy)
>> fplot(P, [0.5, 5])
>> hold on
>> fplot(@(x)1 ./ x, [0.5, 5])
>> legend('插值点', '拉格朗日插值多项式P(x)', 'y=1/x')
|

Neville插值法
Neville插值多项式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| function Q = Neville(xx, yy)
syms x;
n = length(xx);
n = n - 1;
QQ(1, 1) = x;
for k = 0:n
QQ(k + 1, 1) = yy(k + 1);
end
for i = 1:n
for j = 1:i
QQ(i + 1, j + 1) = ((x - xx(i - j +1)) * QQ(i + 1, j) - (x - xx(i +1)) * QQ(i, j)) / (xx(i + 1) - xx(i - j + 1));
end
end
Q = QQ(n + 1, n + 1);
simplify(Q);
Q = matlabFunction(Q);
disp('Neville插值表为:')
QQ
end
|
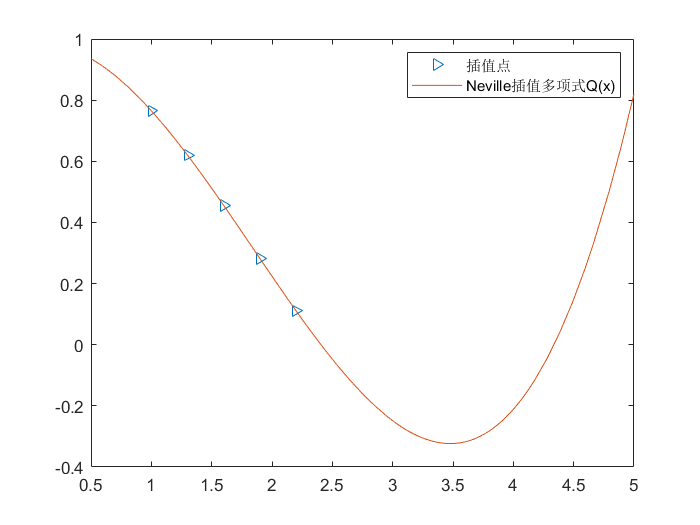
例如:
1
2
3
4
5
6
7
8
| >> xx = [1, 1.3, 1.6, 1.9, 2.2]
>> yy = [0.7651977, 0.6200860, 0.4554022, 0.2818186, 0.1103623]
>> plot(xx, yy, '>')
>> hold on
>> Q = Neville(xx, yy)
>> fplot(Q, [0.5, 5])
>> legend('插值点', 'Neville插值多项式Q(x)')
|

Neville插值表求值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| function QQ = NevilleTable(xx, yy, TOL, x)
n = length(xx);
QQ = zeros(n, n);
for k = 1:n
QQ(k, 1) = yy(k);
end
for i = 2:n
for j = 2:i
QQ(i, j) = ((x - xx(i - j + 1)) * QQ(i, j - 1) - (x - xx(i)) * QQ(i - 1, j - 1)) / (xx(i) - xx(i - j + 1));
end
if abs(QQ(i, i) - QQ(i - 1, i - 1)) < TOL
break
end
end
end
|
例如:
1
2
3
4
5
6
7
8
9
10
11
| >> xx = [1, 1.3, 1.6, 1.9, 2.2]
>> yy = [0.7651977, 0.6200860, 0.4554022, 0.2818186, 0.1103623]
>> NevilleTable(xx, yy, 0.0001, 1.5)
ans =
0.7652 0 0 0 0
0.6201 0.5233 0 0 0
0.4554 0.5103 0.5125 0 0
0.2818 0.5133 0.5113 0.5118 0
0.1104 0.5104 0.5137 0.5118 0.5118
|
牛顿插值法
牛顿插值多项式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| function F = Newton_Divided_Difference(xx, ff)
syms x;
n = length(xx);
n = n - 1;
FF = zeros(n, n);
for k = 0:n
FF(k + 1, 1) = ff(k + 1);
end
for i = 1:n
for j = 1:i
FF(i + 1, j + 1) = (FF(i + 1, j) - FF(i, j)) / (xx(i + 1) - xx(i - j + 1));
end
end
FF
F = FF(1, 1);
for i = 1:n
f = FF(i + 1, i + 1);
for j = 1:i
f = f * (x - xx(j));
end
F = F + f;
end
simplify(F);
F = matlabFunction(F);
end
|
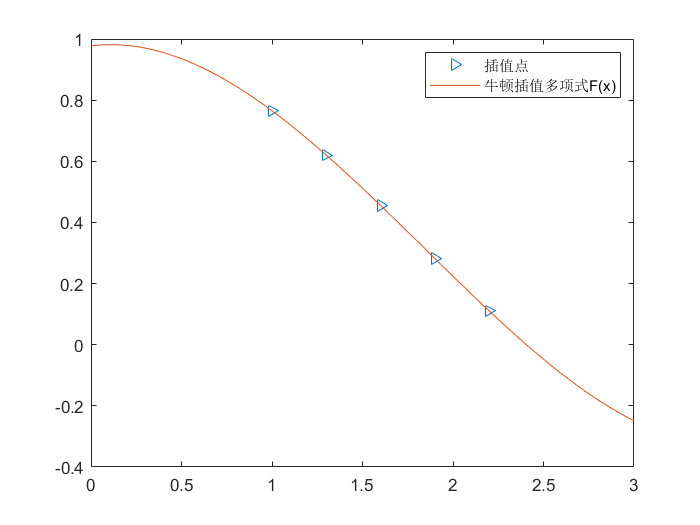
1
2
3
4
5
6
7
8
| >> xx = [1, 1.3, 1.6, 1.9, 2.2]
>> yy = [0.7651977, 0.6200860, 0.4554022, 0.2818186, 0.1103623]
>> plot(xx, yy, '>')
>> hold on
>> F = Newton_Divided_Difference(xx, yy)
>> fplot(F, [0, 3])
>> legend('插值点', '牛顿插值多项式F(x)')
|

牛顿前插公式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| function F_x = Newton_Forward_Difference(F, x_0, n, step_length, TOL, x)
FF = zeros(n + 1, n + 1);
s = (x - x_0) / step_length;
for k = 0:n
xx(k + 1) = x_0 + k * step_length;
yy(k + 1) = F(xx(k + 1));
end
for k = 0:n
FF(k + 1, 1) = yy(k + 1);
end
for i = 1:n
for j = 1:i
FF(i + 1, j + 1) = (FF(i + 1, j) - FF(i, j)) / (xx(i + 1) - xx(i - j + 1));
end
if abs(FF(i + 1, i + 1)) < TOL
break;
end
end
FF
F_x = FF(1, 1);
for i = 1:n
ss = 1;
for j = 1:i
ss = ss * (s - j + 1);
end
f = FF(i + 1, i + 1) * step_length^i * ss;
F_x = F_x + f;
end
fprintf('比较:F(x) = %f', F(x));
end
|
牛顿后插公式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| function F_x = Newton_Backward_Difference(F, x_n, n, step_length, TOL, x)
FF = zeros(n + 1, n + 1);
s = (x - x_n) / step_length;
for k = n:-1:0
xx(k + 1) = x_n - (n - k) * step_length;
yy(k + 1) = F(xx(k + 1));
end
for k = 0:n
FF(k + 1, 1) = yy(k + 1);
end
for i = 1:n
for j = 1:i
FF(n - i + j + 1, j + 1) = (FF(n - i + j + 1, j) - FF(n - i + j, j)) / (xx(n - i + j + 1) - xx(n - i + 1));
end
if abs(FF(n + 1, i + 1)) < TOL
break;
end
end
FF
F_x = FF(n + 1, 1);
for i = 1:n
ss = 1;
for j = 1:i
ss = ss * (s + j - 1);
end
f = FF(n + 1, i + 1) * step_length^i * ss;
F_x = F_x + f;
end
fprintf('比较:F(x) = %f', F(x));
end
|
Stirling
书上没写原理,可以理解成耍流氓吗?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
| function F_x = Stirling(F, x_0, n, step_length, TOL, x)
if mod(n, 2) == 1
n = n - 1;
end
FF = zeros(n + 1, n + 1);
s = (x - x_0) / step_length;
m = n / 2;
xx(m + 1) = x_0;
for k = 1:m
xx(m + 1 + k) = x_0 + k * step_length;
xx(m + 1 - k) = x_0 - k * step_length;
end
for k = 1:n + 1
FF(k, 1) = F(xx(k));
end
mark = n + 1;
for i = 2:n + 1
if mod(i, 2) == 0
for j = 2:i
FF((m + 1) + i / 2, j) = (FF((m + 1) + i / 2, j - 1) - FF((m + 1) + i / 2 - 1, j - 1)) / (xx((m + 1) + i / 2) - xx((m + 1) + i / 2 - (j - 1)));
FF((m + 1) - i / 2 + j - 1, j) = (FF((m + 1) - i / 2 + j - 1, j - 1) - FF((m + 1) - i / 2 + j - 2, j - 1)) / (xx((m + 1) - i / 2 + j - 1) - xx((m + 1) - i / 2));
end
else
FF((m + 1) + (i - 1) / 2, i) = (FF((m + 1) + (i - 1) / 2, i - 1) - FF((m + 1) + (i - 1) / 2 - 1, i - 1)) / (xx((m + 1) + (i - 1) / 2) - xx((m + 1) - (i - 1) / 2));
if abs(FF((m + 1) + (i - 1) / 2, i)) < TOL
mark = i;
break;
end
end
end
F_x = FF(m + 1, 1) + s * step_length * (FF(m + 1, 2) + FF(m + 2, 2)) / 2 + s^2 * step_length^2 * FF(m + 2, 3);
if mark > 3
S1 = 1;
S2 = 1;
for k = 4:n + 1
if mod(k, 2) == 0
S1 = S1 * (s^2 - (k / 2 - 1)^2);
F_x = F_x + (FF((m + 1) + k / 2, k) +FF((m + 1) + k / 2 - 1, k)) * (s * S1) * step_length^(k - 1) / 2;
else
S2 = S2 * (s^2 - (k / 2 - 1/2)^2);
F_x = F_x + FF((m + 1) + (k - 1) / 2, k) * (s^2 * S2) * step_length^(k - 1);
end
end
end
end
|
比较一下下面的两个差距,明白前插与后插的区别,就近原则嘛~
1
2
3
4
5
6
7
| >> F = @(x) sin(x)
>> Newton_Forward_Difference(F, 0, 8, 0.3, 0.01, 0.2)
>> Newton_Forward_Difference(F, 0, 8, 0.3, 0.01, 2)
>> Newton_Backward_Difference(F, 2, 8, 0.3, 0.01, 1.8)
>> Newton_Backward_Difference(F, 2, 8, 0.3, 0.01, 0.2)
|
Hermite插值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| function H = Hermite(xx, ff, dff)
syms x;
n = length(xx);
Q = zeros(2 * n, 2 * n);
n = n - 1;
for k = 1:n + 1
z(2 * k - 1) = xx(k);
z(2 * k) = xx(k);
Q(2 * k - 1, 1) = ff(k);
Q(2 * k, 1) = ff(k);
Q(2 * k, 2) = dff(k);
if k > 1
Q(2 * k - 1, 2) = (Q(2 * k - 1, 1) - Q(2 * k - 2, 1)) / (z(2 * k - 1) - z(2 * k - 2));
end
end
for i = 2:2 * n + 1
for j = 2:i
Q(i + 1, j + 1) = (Q(i + 1, j) - Q(i, j)) / (z(i + 1) - z(i - j + 1));
end
end
H = Q(1, 1);
omega = 1;
for k = 1:2 * n + 1
omega = omega * (x - z(k));
H = H + Q(k + 1, k + 1) * omega;
end
simplify(H);
H = matlabFunction(H);
end
|
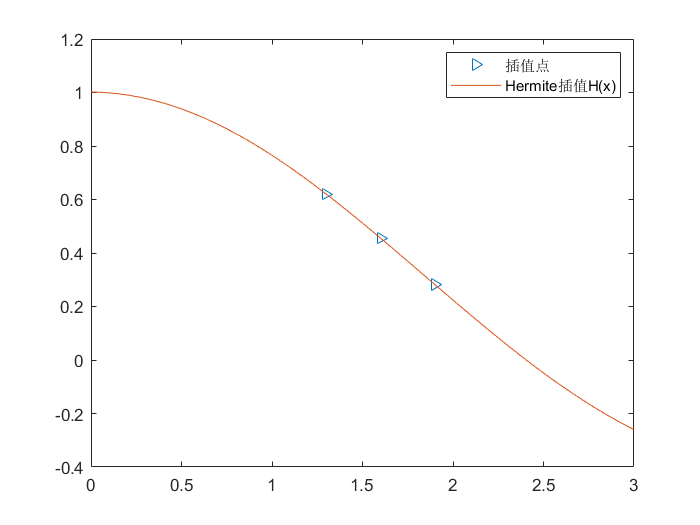
例如:
1
2
3
4
5
6
7
8
9
| >> xx = 1.3:0.3:1.9
>> ff = [0.6200860, 0.4554022, 0.2818186]
>> dff = [-0.5220232, -0.5698959, -0.5811571]
>> plot(xx, ff, '>');
>> hold on;
>> H = Hermite(xx, ff, dff)
>> fplot(H, [0, 3])
>> legend('插值点', 'Hermite插值H(x)')
|

三次样条插值
分段插值
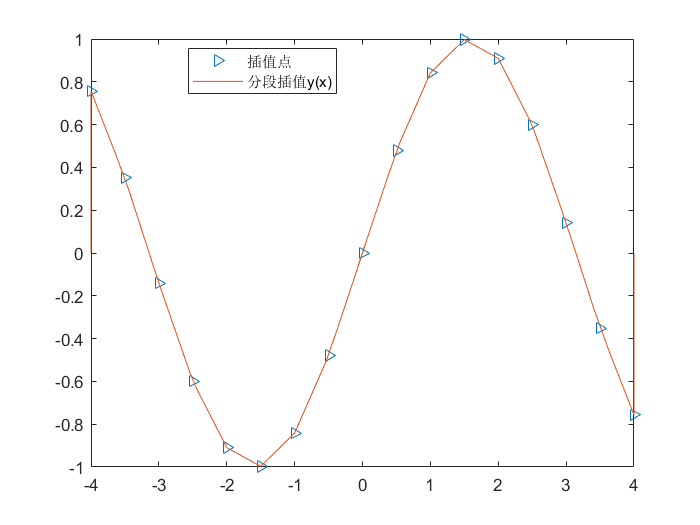
平时用的plot函数就是这样画图的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| function y = piecewise_liner(xx, yy)
syms x;
n = length(xx);
n = n - 1;
y = 0;
for k = 1:n
a = (yy(k + 1) - yy(k)) / (xx(k + 1) - xx(k));
y_k(k) = a * (x - xx(k)) + yy(k);
end
for k = 1:n
y = piecewise(xx(k) <= x <= xx(k + 1), y_k(k), y);
end
end
|
例如:
1
2
3
4
5
6
7
8
9
| >> F = @(x)sin(x)
>> xx = -4:0.5:4
>> yy = F(xx)
>> plot(xx, yy, '>');
>> hold on;
>> y = piecewise_liner(xx, yy)
>> fplot(y, [-4, 4])
>> legend('插值点', '分段插值y(x)')
|

自然二次样条
条件为:
Sj=ai+bi(x−xi)+ci(x−xi)2,其中x∈[xj,xj+1],对于j=0,1,…,n−1成立Sj(xj)=f(xj)且Sj(xj+1)=f(xj+1),对于j=0,1,…,n−1成立Sj+1(xj+1)=Sj(xj+1),对于j=0,1,…,n−2成立Sj+1′(xj+1)=Sj′(xj+1),对于j=0,1,…,n−2成立
附加边界条件:(自然边界)S0′=Sn−1′=0
但是不需要使用Sn−1′=0,使用Sn−1(xn)=f(xn)才能保证最后一个函数过最后一个点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
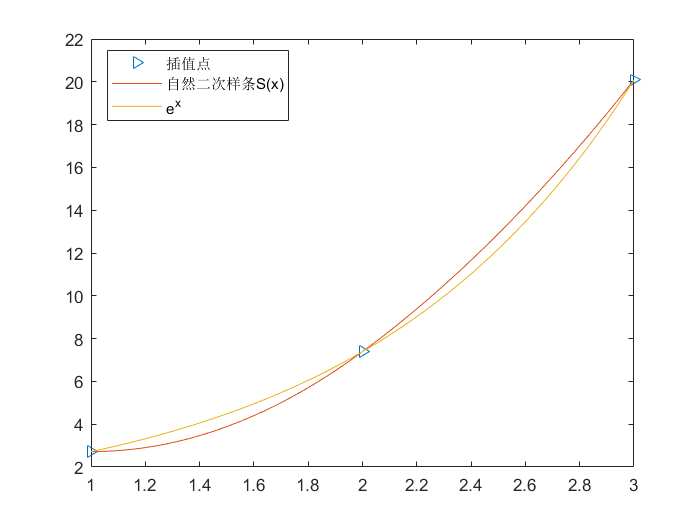
| function S = Quadratic_Splines(xx, yy)
syms x;
n0 = length(xx);
S = 0;
for k = 1:n0
a(k) = yy(k);
end
n = n0 - 1;
for k = 1:n
h(k) = xx(k + 1) - xx(k);
end
b(1) = 0;
for k = 1:n - 1
b(k + 1) = 2 * (a(k + 1) - a(k)) / h(k) - b(k);
c(k) = (b(k + 1) - b(k)) / (2 * h(k));
end
c(n) = (a(n + 1) - a(n) - b(n) * h(n)) / h(n)^2;
for k = 1:n
s(k) = a(k) + b(k) * (x - xx(k)) + c(k) * (x - xx(k))^2;
S = piecewise(xx(k) <= x <= xx(k + 1), s(k), S);
end
end
|
例如:说实话不咋地
1
2
3
4
5
6
7
8
9
10
11
| >> F = @(x)exp(x)
>> xx = 1:3
>> yy = F(xx)
>> plot(xx, yy, '>');
>> hold on;
>> S = Quadratic_Splines(xx, yy)
>> fplot(S, [1, 3])
>> hold on;
>> fplot(@(x)exp(x), [1, 3])
>> legend('插值点', '自然二次样条S(x)','e^x')
|

自然三次样条
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
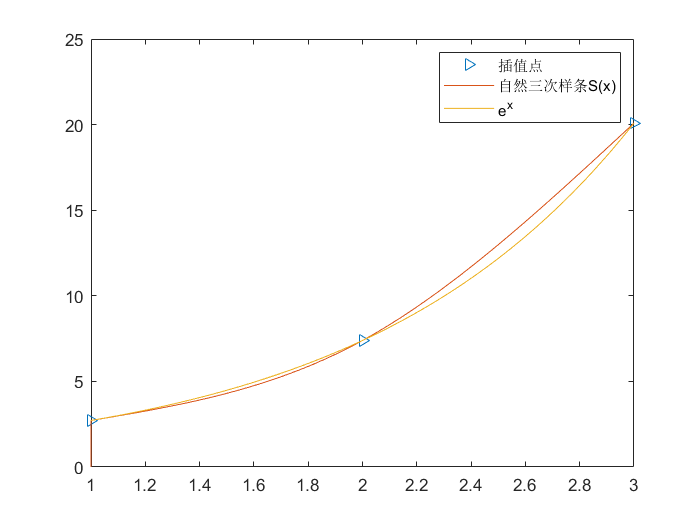
| function S = Natural_Cubic_Spline(xx, yy)
syms x;
n0 = length(xx);
S = 0;
for k = 1:n0
a(k) = yy(k);
end
n = n0 - 1;
for k = 1:n
h(k) = xx(k + 1) - xx(k);
end
for i = 1:n - 1
b(i + 1) = 3 * (a(i + 2) - a(i + 1)) / h(i + 1) - 3 * (a(i + 1) - a(i)) / h(k);
end
l(1) = 1;
u(1) = 0;
z(1) = 0;
for i = 1:n - 1
l(i + 1) = 2 * (xx(i + 2) - xx(i)) - h(i) * u(i);
u(i + 1) = h(i + 1) / l(i + 1);
z(i + 1) = (b(i + 1) - h(i) * z(i)) / l(i + 1);
end
l(n + 1) = 1;
z(n + 1) = 0;
c(n + 1) = 0;
for j = n - 1:-1:0
c(j + 1) = z(j + 1) - u(j + 1) * c(j + 2);
b(j + 1) = (a(j + 2) - a(j + 1)) / h(j + 1) - h(j + 1) * (c(j + 2) + 2 * c(j + 1)) / 3;
d(j + 1) = (c(j + 2) - c(j + 1)) / (3 * (h(j + 1)));
end
for k = 1:n
s(k) = a(k) + b(k) * (x - xx(k)) + c(k) * (x - xx(k))^2 +d(k) * (x - xx(k))^3;
S = piecewise(xx(k) < x <= xx(k + 1), s(k), S);
end
end
|
例如:
1
2
3
4
5
6
7
8
9
10
11
| >> F = @(x)exp(x)
>> xx = 1:3
>> yy = F(xx)
>> plot(xx, yy, '>');
>> hold on;
>> S = Natural_Cubic_Spline(xx, yy)
>> fplot(S, [1, 3])
>> hold on;
>> fplot(@(x)exp(x), [1, 3])
>> legend('插值点', '自然三次样条S(x)','e^x')
|

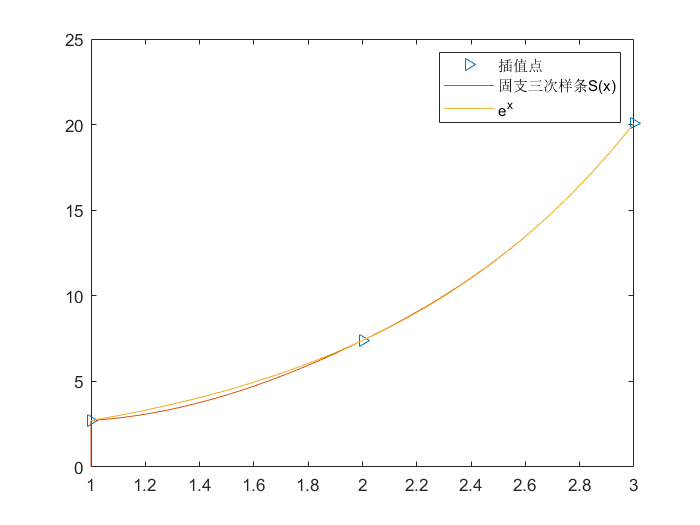
固支三次样条(Clamped Cubic Spline)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
| function S = Clamped_Cubic_Spline(xx, yy, df_0, df_n)
syms x;
n0 = length(xx);
for k = 1:n0
a(k) = yy(k);
end
n = n0 - 1;
for k = 1:n
h(k) = xx(k + 1) - xx(k);
end
b(1) = 3 * (a(2) - a(1)) / h(1) -3 * df_0;
b(n + 1) = 3 * df_n - 3 * (a(n + 1) - a(n)) / h(n);
for i = 1:n - 1
b(i + 1) = 3 * (a(i + 2) - a(i + 1)) / h(i + 1) - 3 * (a(i + 1) - a(i)) / h(k)
end
l(1) = 2 * h(1);
u(1) = 0.5;
z(1) = b(1) / l(1);
for i = 1:n - 1
l(i + 1) = 2 * (xx(i + 2) - xx(i)) - h(i) * u(i);
u(i + 1) = h(i + 1) / l(i + 1);
z(i + 1) = (b(i + 1) - h(i) * z(i)) / l(i + 1);
end
l(n + 1) = h(n) * (2 - u(n));
z(n + 1) = (b(n + 1) - h(n) * z(n)) / l(n + 1);
c(n + 1) = z(n + 1);
for j = n - 1:-1:0
c(j + 1) = z(j + 1) - u(j + 1) * c(j + 2);
b(j + 1) = (a(j + 2) - a(j + 1)) / h(j + 1) - h(j + 1) * (c(j + 2) + 2 * c(j + 1)) / 3;
d(j + 1) = (c(j + 2) - c(j + 1)) / (3 * (h(j + 1)));
end
for k = 1:n
S(k) = a(k) + b(k) * (x - xx(k)) + c(k) * (x - xx(k))^2 +d(k) * (x - xx(k))^3;
simply = simplify(S(k));
s_k = matlabFunction(simply);
fplot(s_k, [xx(k), xx(k + 1)]); hold on;
end
plot(xx, yy, '>'); hold on;
end
|
例如:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| >> F = @(x)exp(x)
>> xx = 1:3
>> yy = F(xx)
>> plot(xx, yy, '>');
>> hold on;
>> f = sym(F)
>> df = diff(f, 1)
>> dF = matlabFunction(df)
>> df_0 = dF(0)
>> df_n = dF(3)
>> S = Clamped_Cubic_Spline(xx, yy, df_0, df_n)
>> fplot(S, [1, 3])
>> hold on;
>> fplot(@(x)exp(x), [1, 3])
>> legend('插值点', '固支三次样条S(x)','e^x')
|

贝塞尔曲线
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| function C = Bezier(xx, yy, xxleft, yyleft, xxright, yyright)
syms t;
n = length(xx);
n = n -1;
for k = 0:n - 1
a_0(k + 1) = xx(k + 1);
b_0(k + 1) = yy(k + 1);
a_1(k + 1) = 3 * (xxleft(k + 1) - xx(k + 1));
b_1(k + 1) = 3 * (yyleft(k + 1) - yy(k + 1));
a_2(k + 1) = 3 * (xx(k + 1) + xxright(k + 1) - 2 * xxleft(k + 1));
b_2(k + 1) = 3 * (yy(k + 1) + yyright(k + 1) - 2 * yyleft(k + 1));
a_3(k + 1) = xx(k + 2) - xx(k + 1) + 3 * xxleft(k + 1) - 3 * xxright(k + 1);
b_3(k + 1) = yy(k + 2) - yy(k + 1) + 3 * yyleft(k + 1) - 3 * yyright(k + 1);
x(k + 1) = a_0 + a_1 * t + a_2 * t^2 + a_3 * t^3;
C(k + 1, 1) = x(k + 1);
line([xx(k+1),xxleft(k+1)],[yy(k+1),yyleft(k+1)]); hold on;
line([xx(k+2),xxright(k+1)],[yy(k+2),yyright(k+1)]); hold on;
y(k + 1) = b_0 + b_1 * t + b_2 * t^2 + b_3 * t^3;
C(k + 1, 2) = y(k + 1);
fplot(x(k+1),y(k+1),[0,1])
end
end
|
觉得这种拟合曲线的方法还不如直接对两个坐标三次样条算了,拉格朗日也比上面的算法强的不知道哪里去了
例如:什么牛马,没有例子!!
数值微分与数值积分
数值微分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| function Numerical_Differentiation(F, x_0, h)
f = sym(F);
df = diff(f, 1);
dF = matlabFunction(df);
df0 = dF(x_0)
df1 = (F(x_0 + h) - F(x_0)) / h;
fprintf('前插公式:df(x_0)=%f\r\n', df1);
error1 = abs(df0 - df1);
fprintf('误差为:error=%f\r\n', error1);
df2 = (-3 * F(x_0) + 4 * F(x_0 + h) - F(x_0 + 2 * h)) / (2 * h);
fprintf('三点端点公式:df(x_0)=%f\r\n', df2);
error2 = abs(df0 - df2);
fprintf('误差为:error=%f\r\n', error2);
df3 = (F(x_0 + h) - F(x_0 - h)) / (2 * h);
fprintf('三点中点公式:df(x_0)=%f\r\n', df3);
error3 = abs(df0 - df3);
fprintf('误差为:error=%f\r\n', error3);
df4 = (F(x_0 - 2 * h) - 8 * F(x_0 - h) + 8 * F(x_0 + h) - F(x_0 + 2 * h)) / (12 * h);
fprintf('五点中点公式:df(x_0)=%f\r\n', df4);
error4 = abs(df0 - df4);
fprintf('误差为:error=%f\r\n', error4);
df5 = (-25 * F(x_0) + 48 * F(x_0 +h) - 36 * F(x_0 + 2 * h) + 16 * F(x_0 + 3 * h) - 3 * F(x_0 + 4 * h)) / (12 * h);
fprintf('五点端点公式:df(x_0)=%f\r\n', df5);
error5 = abs(df0 - df5);
fprintf('误差为:error=%f\r\n', error5);
end
|
例如:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| >> F = @(x)exp(x)
>> Numerical_Differentiation(F, 1, 0.01)
前插公式:df(x_0)=2.731919
误差为:error=0.013637
三点端点公式:df(x_0)=2.718191
误差为:error=0.000091
三点中点公式:df(x_0)=2.718327
误差为:error=0.000045
五点中点公式:df(x_0)=2.718282
误差为:error=0.000000
五点端点公式:df(x_0)=2.718282
误差为:error=0.000000
|
理查德外推
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| function Richardson_Extrapolation(F, x_0, h, n, TOL)
f = sym(F);
df = diff(f, 1);
dF = matlabFunction(df);
df0 = dF(x_0)
for k = 1:n
N1(k, 1) = (F(x_0 + h / k) - F(x_0 - h / k)) / (2 * h / k);
N2(k, 1) = (F(x_0 + h / k) - F(x_0 - h / k)) / (2 * h / k);
end
for i = 2:n
for j = i:n
N1(j, i) = N1(j, i - 1) + (N1(j, i - 1) - N1(j - 1, i - 1)) / (2^(i - 1) - 1);
N2(j, i) = N1(j, i - 1) + (N1(j, i - 1) - N1(j - 1, i - 1)) / (4^(i - 1) - 1);
end
if abs(N1(i, i) - N1(i - 1, i - 1)) < TOL
break;
end
end
N1
N2
end
|
例如:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| >> F = @(x)exp(x)
>> Richardson_Extrapolation(F, 1, 0.1, 6, 0.0001)
N1 =
2.7228 0 0 0 0
2.7194 2.7160 0 0 0
2.7188 2.7182 2.7189 0 0
2.7186 2.7183 2.7184 2.7183 0
2.7185 2.7184 2.7184 2.7184 2.7184
2.7184 2.7184 2.7183 2.7183 2.7183
N2 =
2.7228 0 0 0 0
2.7194 2.7183 0 0 0
2.7188 2.7186 2.7183 0 0
2.7186 2.7185 2.7184 2.7184 0
2.7185 2.7184 2.7184 2.7184 2.7184
2.7184 2.7184 2.7184 2.7183 2.7183
|
数值积分
闭合式牛顿科特斯公式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| function I = Closed_Newton_Cotes(F, n, endpoint_a, endpoint_b)
syms x;
I = 0;
P = 0;
h = (endpoint_b - endpoint_a) / n;
for i = 0:n
L = 1;
for j = 0:n
if j == i
continue;
end
L = L * (x - (endpoint_a + j * h)) / ((endpoint_a + i * h) - (endpoint_a + j * h));
end
p = sym2poly(L);
q = polyint(p);
a = diff(polyval(q, [endpoint_a endpoint_b]));
P = P + L * F(endpoint_a + i * h);
I = I + a * F(endpoint_a + i * h);
end
end
|
例如:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| >> F = @(x)sin(x)
>> Closed_Newton_Cotes(F, 1, 0, pi / 4)
ans =
0.2777
>> Closed_Newton_Cotes(F, 2, 0, pi / 4)
ans =
0.2929
>> Closed_Newton_Cotes(F, 3, 0, pi / 4)
ans =
0.2929
>> Closed_Newton_Cotes(F, 4, 0, pi / 4)
ans =
0.2929
|
开放式牛顿科特斯公式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| function I = Open_Newton_Cotes(F, n, endpoint_a, endpoint_b)
syms x;
I = 0;
P = 0;
h = (endpoint_b - endpoint_a) / (n + 2);
for i = 0:n
L = 1;
for j = 0:n
if j == i
continue;
end
L = L * (x - (endpoint_a + (j + 1) * h)) / ((endpoint_a + (i + 1) * h) - (endpoint_a + (j + 1) * h));
end
if L ~= 1
p = sym2poly(L);
q = polyint(p);
a = diff(polyval(q, [endpoint_a endpoint_b]));
else
a = endpoint_b - endpoint_a;
end
P = P + L * F(endpoint_a + (i + 1) * h);
I = I + a * F(endpoint_a + (i + 1) * h);
end
end
|
例如:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| >> F = @(x)sin(x)
>> Open_Newton_Cotes(F, 0, 0, pi / 4)
ans =
0.3006
>> Open_Newton_Cotes(F, 1, 0, pi / 4)
ans =
0.2980
>> Open_Newton_Cotes(F, 2, 0, pi / 4)
ans =
0.2929
>> Open_Newton_Cotes(F, 3, 0, pi / 4)
ans =
0.2929
|
复合数值积分
复化Simpson’s Rule
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| function XI = Composite_Simpson(F, n, endpoint_a, endpoint_b)
if mod(n, 2) == 1
n = n + 1;
end
h = (endpoint_b - endpoint_a) / n;
XI0 = F(endpoint_a) + F(endpoint_b);
XI1 = 0;
XI2 = 0;
for i = 1:n - 1
X = endpoint_a + i * h;
if mod(i, 2) == 0
XI2 = XI2 + F(X);
else
XI1 = XI1 + F(X);
end
end
XI = h / 3 * (XI0 + 2 * XI2 + 4 * XI1);
end
|
例如:
1
2
3
4
5
6
| >> F = @(x)sin(x)
>> Composite_Simpson(F, 8, 0, 4)
ans =
1.6542
|
复化梯形公式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| function XI = Composite_Trapezoidal(F, n, endpoint_a, endpoint_b)
h = (endpoint_b - endpoint_a) / n;
XI0 = F(endpoint_a) + F(endpoint_b);
XI1 = 0;
for i = 1:n - 1
XI1 = XI1 + F(endpoint_a + i * h);
end
XI = h / 2 * (XI0 + 2 * XI1);
end
|
例如:
1
2
3
4
5
6
| >> F = @(x)sin(x)
>> Composite_Trapezoidal(F, 8, 0, 4)
ans =
1.6190
|
复化中点公式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| function XI = Composite_Midpoint(F, n, endpoint_a, endpoint_b)
if mod(n, 2) == 1
n = n + 1;
end
h = (endpoint_b - endpoint_a) / (n + 2);
XI1 = 0;
for i = 0:n / 2
XI1 = XI1 + F(endpoint_a + (2 * i + 1) * h);
end
XI = 2 * h * XI1;
end
|
例如:
1
2
3
4
5
6
| >> F = @(x)sin(x)
>> Composite_Midpoint(F, 8, 0, 4)
ans =
1.6986
|
龙贝格积分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| function R = Romberg(F, n, endpoint_a, endpoint_b, TOL)
h(1) = endpoint_b - endpoint_a;
R(1, 1) = h / 2 * (F(endpoint_a) + F(endpoint_b));
for i = 2:n
sum_f = 0;
K = 2^(i - 2);
h(i) = h(i - 1) / 2;
for k = 1:K
sum_f = sum_f + F(endpoint_a + (2 * k - 1) * h(i));
end
R(i, 1) = 1/2 * (R(i - 1, 1) + h(i - 1) * sum_f);
for j = 2:i
R(i, j) = R(i, j - 1) + (R(i, j - 1) - R(i - 1, j - 1)) / (4^(j - 1) - 1);
end
if abs(R(i, i) - R(i - 1, i - 1)) < TOL
break;
end
end
end
|
例如:
1
2
3
4
5
6
7
8
9
10
11
| >> F = @(x)sin(x)
>> Romberg(F, 6, 0, pi, 0.00000001)
ans =
0.0000 0 0 0 0 0
1.5708 2.0944 0 0 0 0
1.8961 2.0046 1.9986 0 0 0
1.9742 2.0003 2.0000 2.0000 0 0
1.9936 2.0000 2.0000 2.0000 2.0000 0
1.9984 2.0000 2.0000 2.0000 2.0000 2.0000
|
自适应求积
堆栈法
算法本质上是属于迭代,书上把迭代转换成了堆栈
理解:在数据结构我们学习了二叉树,其中三种遍历方法:先序遍历,中序遍历以及后序遍历。例如先序遍历是在每一个节点上,先访问该节点,然后依次访问左节点与右节点。
而在这个算法中,我们对每一个积分区间进行折半,先对右半区间进行积分计算,再对左半区间进行积分计算。如果在其中一个积分区间不满足条件∣∣Si(a,b)−Si(a,2a+b)−Si(2a+b,b)∣∣<TOLi,则继续细分子区间,并且优先计算右半区间。
因此取名为右半序遍历自适应积分算法不是不行,当然稍微改一下也可以成为左半序区间遍历算法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
| function APP = Adaptive_Quadrature(F, TOL, N, endpoint_a, endpoint_b)
APP = 0;
i = 1;
tol(i) = 10 * TOL;
a(i) = endpoint_a;
h(i) = (endpoint_b - endpoint_a) / 2;
FA(i) = F(a(i));
FC(i) = F(a(i) + h(i));
FB(i) = F(endpoint_b);
S(i) = h(i) / 3 * (FA(i) + 4 * FC(i) + FB(i));
mark(i) = 1;
while i > 0
FD = F(a(i) + h(i) / 2);
FE = F(a(i) + 3/2 * h(i));
S1 = h(i) / 6 * (FA(i) + 4 * FD + FC(i));
S2 = h(i) / 6 * (FC(i) + 4 * FE + FB(i));
v1 = a(i);
v2 = FA(i);
v3 = FC(i);
v4 = FB(i);
v5 = h(i);
v6 = tol(i);
v7 = S(i);
v8 = mark(i);
i = i - 1;
if abs(S1 +S2 -v7) < v6
APP = APP + S1 + S2;
else
if v8 > N
disp('超过最大迭代次数');
break;
else
i = i + 1;
a(i) = v1 + v5;
FA(i) = v3;
FC(i) = FE;
FB(i) = v4;
h(i) = v5 / 2;
tol(i) = v6 / 2;
S(i) = S2;
mark(i) = v8 + 1;
i = i + 1;
a(i) = v1;
FA(i) = v2;
FC(i) = FD;
FB(i) = v3;
h(i) = h(i - 1);
tol(i) = tol(i - 1);
S(i) = S1;
mark(i) = mark(i - 1);
end
end
end
end
|
例如:
1
2
3
4
5
6
| >> F = @(x)(100 / x^2) * sin(10 / x)
>> Adaptive_Quadrature(F, 0.000001, 1000000, 1, 3)
ans =
-1.4260
|
递归法
显然递归法代码简洁(不是一点两点的简洁),且方便理解,但是这里没有设置迭代次数上限
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| function I = Adaptive_Quadrature_Recursion(F, TOL, endpoint_a, endpoint_b)
h = (endpoint_b - endpoint_a) / 2;
FA = F(endpoint_a);
FC = F(endpoint_a + h);
FB = F(endpoint_b);
S_0 = h / 3 * (FA +4 * FC + FB);
FD = F(endpoint_a + h / 2);
FE = F(endpoint_a + 3 * h / 2);
S_1 = h / 6 * (FA + 4 * FD + FC);
S_2 = h / 6 * (FC + 4 * FE + FB);
if abs(S_0 - S_1 - S_2) < TOL
I = S_0;
else
I = Adaptive_Quadrature_Recursion(F, TOL / 2, endpoint_a, endpoint_a + h) + Adaptive_Quadrature_Recursion(F, TOL / 2, endpoint_a + h, endpoint_b);
end
end
|
例如:
1
2
3
4
5
6
| >> F = @(x)(100 / x^2) * sin(10 / x)
>> Adaptive_Quadrature_Recursion(F, 0.00001, 1, 3)
ans =
-1.4260
|
多重积分
Simpson二重积分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| function I = Simpson_Double_Integral(F, c, d, n, m, endpoint_a, endpoint_b)
h = (endpoint_b - endpoint_a) / n;
J1 = 0;
J2 = 0;
J3 = 0;
for i = 0:n
x_i = endpoint_a + i * h;
k = (d(x_i) - c(x_i)) / m;
K1 = F(x_i, c(x_i)) + F(x_i, d(x_i));
K2 = 0;
K3 = 0;
for j = 1:m - 1
y_i = c(x_i) + j * k;
Q = F(x_i, y_i);
if mod(j, 2) == 0
K2 = K2 + Q;
else
K3 = K3 + Q;
end
end
L = k / 3 * (K1 + 2 * K2 +4 * K3);
if i == 0 || i == n
J1 = J1 + L;
elseif mod(i, 2) == 0
J2 = J2 + L;
else
J3 = J3 + L;
end
end
I = h / 3 * (J1 +2 * J2 +4 * J3);
end
|
例如:
1
2
3
4
5
6
7
8
| >> F = @(x, y)exp(y / x)
>> c = @(x)x^3
>> d = @(x)x^2
>> Simpson_Double_Integral(F, c, d, 10, 10, 0.1, 0.5)
ans =
0.0333
|
瑕积分
方法只局限于类似于$$\int_{a}^{b} \frac{dx}{(x-a)^p}$$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| function I = Improper(F, endpoint_a, endpoint_b)
syms x;
f = F(x);
[numerator, denominator] = numden(sym(f));
dg = numerator;
dG = matlabFunction(dg);
p = simplify(log(denominator) / log(x - endpoint_a));
I = dG(endpoint_a) / (1 - p) * (endpoint_b - endpoint_a)^(1 - p);
Taylor = dG(endpoint_a);
for k = 1:4
dg = diff(numerator, k);
dG = matlabFunction(dg);
Taylor = Taylor + dG(endpoint_a) * (x - endpoint_a)^k / factorial(k);
I = I + dG(endpoint_a) / (factorial(k) * (k + 1 - p)) * (endpoint_b - endpoint_a)^(k + 1 - p);
end
G(x) = piecewise(endpoint_a < x <= endpoint_b, (numerator - Taylor) / denominator, x == endpoint_a, 0);
I = I + Adaptive_Quadrature(G, 0.00000001, 10000000, endpoint_a, endpoint_b);
I = double(I);
end
|
例如:
1
2
3
4
5
6
| >> F=@(x)exp(x)/x^0.5
>> Improper(F, 0, 1)
ans =
2.9253
|
常微分方程的初值问题
欧拉步长法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| function [t, omega] = Euler(F, N, y_0, endpoint_a, endpoint_b)
h = (endpoint_b - endpoint_a) / N;
t(1) = endpoint_a;
omega(1) = y_0;
for i = 1:N
omega(i + 1) = omega(i) + h * F(t(i), omega(i));
t(i + 1) = endpoint_a + i * h;
end
end
|
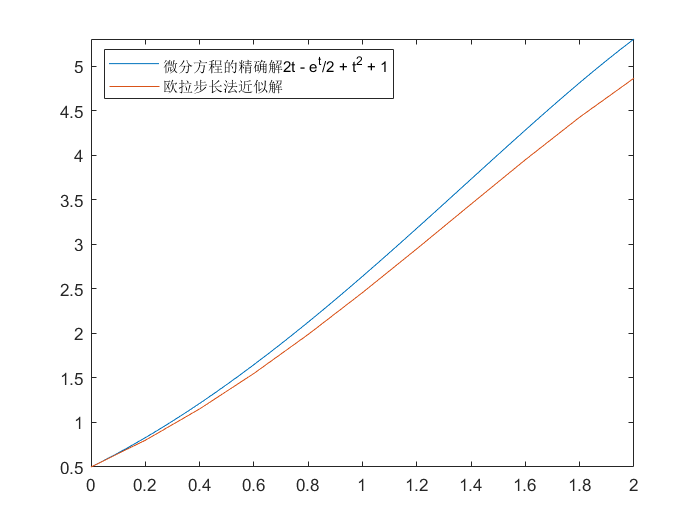
例如:
1
2
3
4
5
6
7
8
| >> y = dsolve('Dy - y + t^2 - 1 = 0', 'y(0)=0.5', 't')
>> fplot(y,[0, 2])
>> hold on
>> F = @(t, y)y - t^2 + 1
>> [t, omega] = Euler(F, 10, 0.5, 0, 2)
>> plot(t, omega);
>> legend('微分方程的精确解2t - e^t/2 + t^2 + 1', '欧拉步长法近似解')
|

高阶泰勒方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| function [t, u] = Taylor(F, n, N, y_0, endpoint_a, endpoint_b)
syms x y;
h = (endpoint_b - endpoint_a) / N;
t(1) = endpoint_a;
u(1) = y_0;
f = F(x, y);
df = f;
T_n = f;
for k = 1:n - 1
df = diff(df, x) + diff(df, y) * f;
T_n = T_n + h^k * df / factorial(k + 1);
end
T = matlabFunction(T_n);
for i = 1:N
u(i + 1) = u(i) + h * T(t(i), u(i));
t(i + 1) = endpoint_a + i * h;
end
end
|
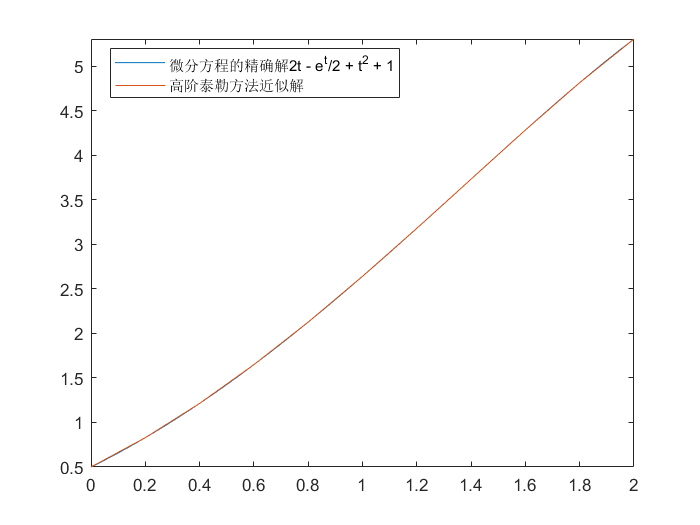
例如:
1
2
3
4
5
6
7
8
| >> y = dsolve('Dy - y + t^2 - 1 = 0', 'y(0)=0.5', 't')
>> fplot(y,[0, 2])
>> hold on
>> F = @(t, y)y - t^2 + 1
>> [t, u] = Taylor(F, 4, 10, 0.5, 0, 2)
>> plot(t, u);
>> legend('微分方程的精确解2t - e^t/2 + t^2 + 1', '高阶泰勒方法近似解')
|

龙格库达方法
Midpoint Method
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| function [t, omega] = Midpoint_Method(F, N, y_0, endpoint_a, endpoint_b)
h = (endpoint_b - endpoint_a) / N;
t(1) = endpoint_a;
omega(1) = y_0;
for i = 1:N
omega(i + 1) = omega(i) + h * F(t(i) + h / 2, omega(i) + h * F(t(i), omega(i)) / 2);
t(i + 1) = endpoint_a + i * h;
end
end
|
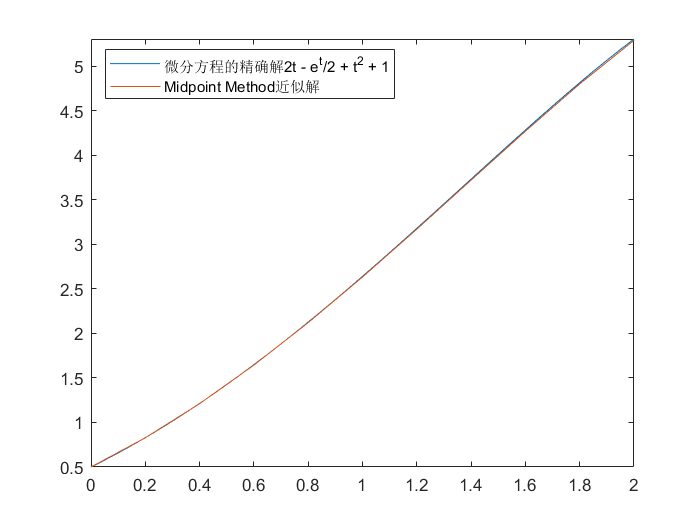
例如:
1
2
3
4
5
6
7
8
| >> y = dsolve('Dy - y + t^2 - 1 = 0', 'y(0)=0.5', 't')
>> fplot(y,[0, 2])
>> hold on
>> F = @(t, y)y - t^2 + 1
>> [t, u] = Midpoint_Method(F, 10, 0.5, 0, 2)
>> plot(t, u);
>> legend('微分方程的精确解2t - e^t/2 + t^2 + 1', 'Midpoint Method近似解')
|

Modified Euler
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| function [t, omega] = Modified_Euler(F, N, y_0, endpoint_a, endpoint_b)
h = (endpoint_b - endpoint_a) / N;
t(1) = endpoint_a;
omega(1) = y_0;
for i = 1:N
omega(i + 1) = omega(i) + h / 2 * (F(t(i), omega(i)) + F(t(i) + h, omega(i) + h * F(t(i), omega(i))));
t(i + 1) = endpoint_a + i * h;
end
plot(t, omega);
end
|
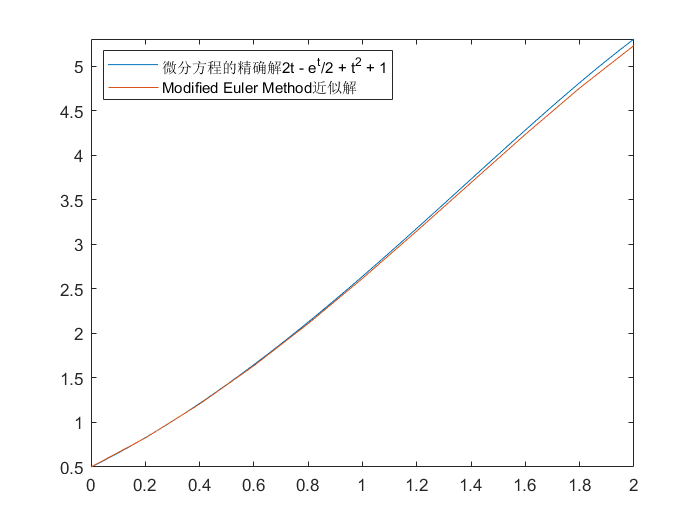
例如:
1
2
3
4
5
6
7
8
| >> y = dsolve('Dy - y + t^2 - 1 = 0', 'y(0)=0.5', 't')
>> fplot(y,[0, 2])
>> hold on
>> F = @(t, y)y - t^2 + 1
>> [t, u] = Modified_Euler(F, 10, 0.5, 0, 2)
>> plot(t, u);
>> legend('微分方程的精确解2t - e^t/2 + t^2 + 1', 'Modified Euler Method近似解')
|

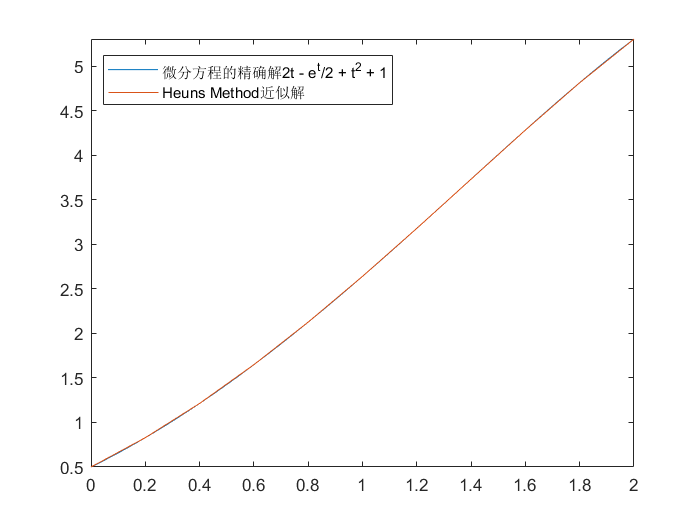
Heun’s Method
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| function [t, omega] = Heun(F, N, y_0, endpoint_a, endpoint_b)
h = (endpoint_b - endpoint_a) / N;
t(1) = endpoint_a;
omega(1) = y_0;
for i = 1:N
omega(i + 1) = omega(i) + h / 4 * (F(t(i), omega(i)) + 3 * F(t(i) + 2 * h / 3, omega(i) + 2 * h / 3 * F(t(i) + h / 3, omega(i) + h / 3 * F(t(i), omega(i)))));
t(i + 1) = endpoint_a + i * h;
end
end
|
例如:
1
2
3
4
5
6
7
8
| >> y = dsolve('Dy - y + t^2 - 1 = 0', 'y(0)=0.5', 't')
>> fplot(y,[0, 2])
>> hold on
>> F = @(t, y)y - t^2 + 1
>> [t, u] = Heun(F, 10, 0.5, 0, 2)
>> plot(t, u);
>> legend('微分方程的精确解2t - e^t/2 + t^2 + 1', 'Heuns Method近似解')
|

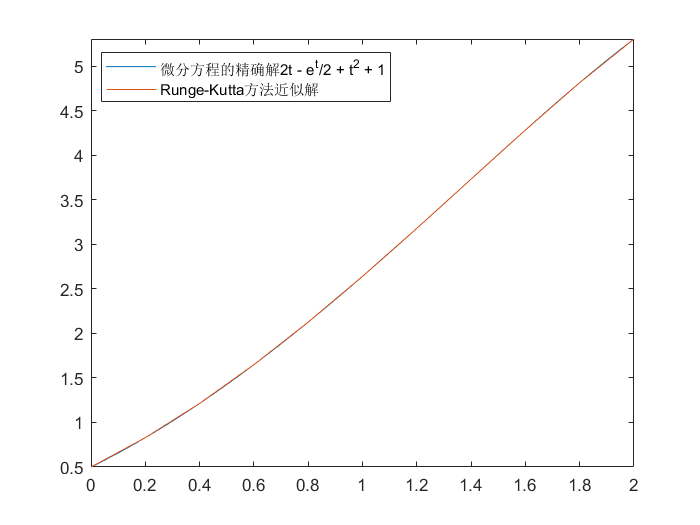
Runge-Kutta
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| function [t, omega] = Runge_Kutta(F, N, y_0, endpoint_a, endpoint_b)
h = (endpoint_b - endpoint_a) / N;
t(1) = endpoint_a;
omega(1) = y_0;
for i = 1:N
k1 = h * F(t(i), omega(i));
k2 = h * F(t(i) + h / 2, omega(i) + k1 / 2);
k3 = h * F(t(i) + h / 2, omega(i) + k2 / 2);
k4 = h * F(t(i) + h, omega(i) + k3);
omega(i + 1) = omega(i) + (k1 + 2 * k2 + 2 * k3 + k4) / 6;
t(i + 1) = endpoint_a + i * h;
end
end
|
例如:
1
2
3
4
5
6
7
8
| >> y = dsolve('Dy - y + t^2 - 1 = 0', 'y(0)=0.5', 't')
>> fplot(y,[0, 2])
>> hold on
>> F = @(t, y)y - t^2 + 1
>> [t, u] = Runge_Kutta(F, 10, 0.5, 0, 2)
>> plot(t, u);
>> legend('微分方程的精确解2t - e^t/2 + t^2 + 1', 'Runge-Kutta方法近似解')
|

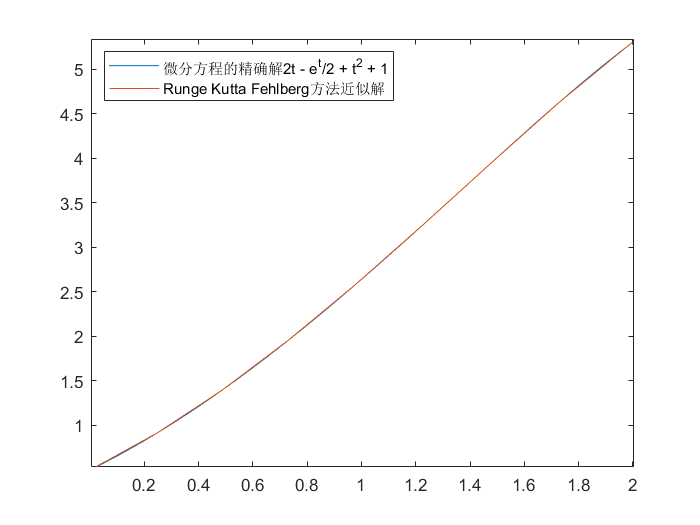
Runge Kutta Fehlberg
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| function [t, omega] = Runge_Kutta_Fehlberg(F, y_0, TOL, hmax, hmin, endpoint_a, endpoint_b)
h = hmax
t(1) = endpoint_a;
omega(1) = y_0;
flag = 1;
i = 1;
while flag == 1
k1 = h * F(t(i), omega(i));
k2 = h * F(t(i) + h / 4, omega(i) + k1 / 4);
k3 = h * F(t(i) + 3 * h / 8, omega(i) +3 * k1 / 32 + 9 * k2 / 32);
k4 = h * F(t(i) +12 * h / 13, omega(i) +1932 * k1 / 2197 - 7200 * k2 / 2197 +7296 * k3 / 2197);
k5 = h * F(t(i) +h, omega(i) +439 * k1 / 216 - 8 * k2 + 3680 * k3 / 513 -845 * k4 / 4104);
k6 = h * F(t(i) +h / 2, omega(i) -8 * k1 / 27 + 2 * k2 - 3544 * k3 / 2565 +1859 * k4 / 4104 - 11 * k5 / 40);
R = abs(k1 / 360 - 128 * k3 / 4275 - 2197 * k4 / 75240 + k5 / 50 + 2 * k6 / 55) / h;
if R < TOL
omega(i + 1) = omega(i) + 25 * k1 / 216 + 1408 * k3 / 2565 + 2197 * k4 / 4104 - k5 / 5;
t(i + 1) = t(i) + h;
i = i + 1;
end
q = (TOL / (2 * R))^0.25;
if q <= 0.1
h = h / 10;
elseif q >= 4
h = 4 * h;
else
h = q * h;
end
if h > hmax
h = hmax;
end
if t(i) >= endpoint_b
flag = 0;
elseif t(i) + h > endpoint_b
h = endpoint_b - t(i);
elseif h < hmin
flag = 0;
disp('h小于hmin,无法进行控制');
end
end
end
|
例如:
1
2
3
4
5
6
7
8
| >> y = dsolve('Dy - y + t^2 - 1 = 0', 'y(0)=0.5', 't')
>> fplot(y,[0, 2])
>> hold on
>> F = @(t, y)y - t^2 + 1
>> [t, u] = Runge_Kutta_Fehlberg(F,0.5,0.00001,0.25,0.01,0,2)
>> plot(t, u);
>> legend('微分方程的精确解2t - e^t/2 + t^2 + 1', 'Runge Kutta Fehlberg方法近似解')
|

多步法
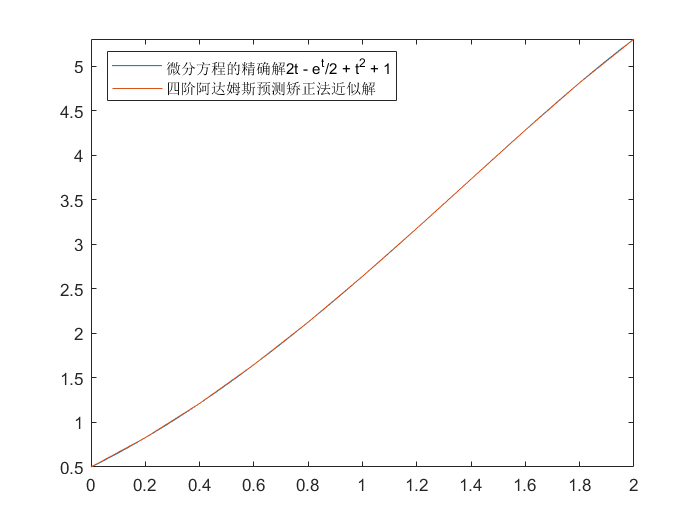
四阶阿达姆斯预测矫正法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| function [t, omega] = Adams_Fourth_Order_Predictor_Corrector(F, N, y_0, endpoint_a, endpoint_b)
h = (endpoint_b - endpoint_a) / N;
t(1) = endpoint_a;
omega(1) = y_0;
for i = 1:3
k1 = h * F(t(i), omega(i));
k2 = h * F(t(i) + h / 2, omega(i) + k1 / 2);
k3 = h * F(t(i) + h / 2, omega(i) + k2 / 2);
k4 = h * F(t(i) + h, omega(i) + k3);
omega(i + 1) = omega(i) + (k1 + 2 * k2 + 2 * k3 + k4) / 6;
t(i + 1) = endpoint_a + i * h;
end
for i = 4:N
t(i + 1) = endpoint_a + i * h;
omega_predictor = omega(i) + h * (55 * F(t(i), omega(i)) - 59 * F(t(i - 1), omega(i - 1)) + 37 * F(t(i - 2), omega(i - 2)) - 9 * F(t(i - 3), omega(i - 3))) / 24;
omega(i + 1) = omega(i) + h * (9 * F(t(i + 1), omega_predictor) + 19 * F(t(i), omega(i)) - 5 * F(t(i - 1), omega(i - 1)) + F(t(i - 2), omega(i - 2))) / 24;
end
end
|
例如:
1
2
3
4
5
6
7
8
| >> y = dsolve('Dy - y + t^2 - 1 = 0', 'y(0)=0.5', 't')
>> fplot(y,[0, 2])
>> hold on
>> F = @(t, y)y - t^2 + 1
>> [t, u] = Adams_Fourth_Order_Predictor_Corrector(F, 10, 0.5, 0, 2)
>> plot(t, u);
>> legend('微分方程的精确解2t - e^t/2 + t^2 + 1', '四阶阿达姆斯预测矫正法近似解')
|

可变步长的多步法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
| function [t, omega] = Adams_Variable_Step_Size(F, y_0, TOL, hmax, hmin, endpoint_a, endpoint_b)
flag = 1;
h = hmax;
omega(1) = y_0;
t(1) = endpoint_a;
[tt, uu] = RK4(F, h, omega(1), t(1));
for j = 2:4
t(j) = tt(j);
omega(j) = uu(j);
end
i = 5;
ti = t(4) + h;
if ti > endpoint_b
disp('hmax过大');
end
while ti <= endpoint_b
t(i) = ti;
omega_predictor = omega(i - 1) + h * (55 * F(t(i - 1), omega(i - 1)) - 59 * F(t(i - 2), omega(i - 2)) + 37 * F(t(i - 3), omega(i - 3)) - 9 * F(t(i - 4), omega(i - 4))) / 24;
omega_corrector = omega(i - 1) + h * (9 * F(t(i), omega_predictor) + 19 * F(t(i - 1), omega(i - 1)) - 5 * F(t(i - 2), omega(i - 2)) + F(t(i - 3), omega(i - 3))) / 24;
delta = 19 * abs(omega_predictor - omega_corrector) / (270 * h);
if delta < TOL
omega(i) = omega_corrector;
if ti == endpoint_b
break;
end
i = i + 1;
if delta < TOL / 10
q = (TOL / (2 * delta))^0.25;
if q > 4
h = 4 * h;
else
h = q * h;
end
if h > hmax
h = hmax;
end
if t(i - 1) + 4 * h > endpoint_b
h = (endpoint_b - t(i - 1)) / 4;
end
[tt, uu] = RK4(F, h, omega(i - 1), t(i - 1));
for j = i:i + 2
t(j) = tt(j - i + 2);
omega(j) = uu(j - i + 2);
end
i = i + 3;
end
if t(i - 1) + h > endpoint_b
h = (endpoint_b - t(i - 1)) / 4;
[tt, uu] = RK4(F, h, omega(i - 1), t(i - 1));
for j = i:i + 2
t(j) = tt(j - i + 2);
omega(j) = uu(j - i + 2);
end
i = i + 3;
end
else
q = (TOL / (2 * delta))^0.25;
if q < 0.1
h = 0.1 * h;
else
h = q * h;
end
if h < hmin
disp('h小于hmin,无法进行控制');
flag = 0;
break;
else
i = i - 3;
[tt, uu] = RK4(F, h, omega(i - 1), t(i - 1));
for j = i:i + 2
t(j) = tt(j - i + 2);
omega(j) = uu(j - i + 2);
end
i = i + 3;
end
end
ti = t(i - 1) + h;
end
end
function [t, omega] = RK4(F, h, y_0, endpoint_a)
t(1) = endpoint_a;
omega(1) = y_0;
for i = 1:3
k1 = h * F(t(i), omega(i));
k2 = h * F(t(i) + h / 2, omega(i) + k1 / 2);
k3 = h * F(t(i) + h / 2, omega(i) + k2 / 2);
k4 = h * F(t(i) + h, omega(i) + k3);
omega(i + 1) = omega(i) + (k1 + 2 * k2 + 2 * k3 + k4) / 6;
t(i + 1) = endpoint_a + i * h;
end
end
|
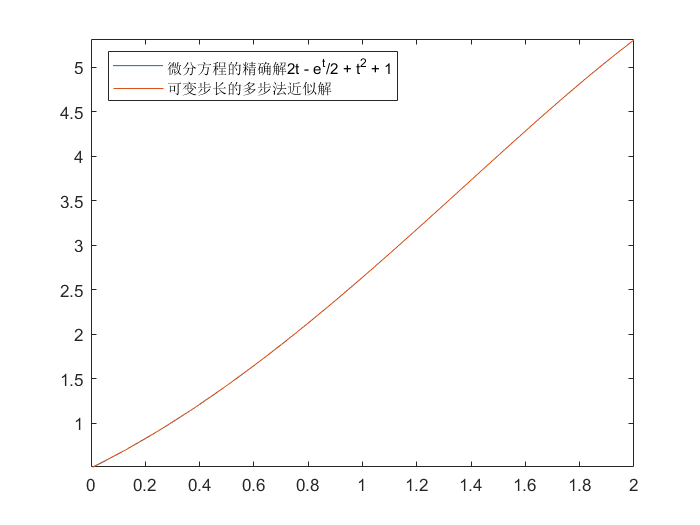
例如:
1
2
3
4
5
6
7
8
| >> y = dsolve('Dy - y + t^2 - 1 = 0', 'y(0)=0.5', 't')
>> fplot(y,[0, 2])
>> hold on
>> F = @(t, y)y - t^2 + 1
>> [t, u] = Adams_Variable_Step_Size(F,0.5,0.00001,0.25,0.01,0,2)
>> plot(t, u);
>> legend('微分方程的精确解2t - e^t/2 + t^2 + 1', '可变步长的多步法近似解')
|

外推法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
| function [t, omega] = Extrapolation(F, y_0, TOL, hmax, hmin, endpoint_a, endpoiny_b)
NK = [2, 4, 6, 8, 12, 16, 24, 32];
t(1) = endpoint_a;
omega(1) = y_0;
n = 1;
T0 = endpoint_a;
W0 = y_0;
h = hmax;
flag = 1;
for i = 1:7
for j = 1:i
Q(i, j) = (NK(i + 1) / NK(i - j + 1))^2;
end
end
while flag == 1
k = 1;
nflag = 0;
while k <= 8 && nflag == 0
h_k = h / NK(k);
T = T0;
W2 = W0;
W3 = W2 + h_k * F(T, W2);
T = T0 + h_k;
for j = 1:NK(k) - 1
W1 = W2;
W2 = W3;
W3 = W1 + 2 * h_k * F(T, W2);
T = T0 + (j + 1) * h_k;
end
y(k, 1) = (W3 + (W2 + h_k * F(T, W3))) / 2;
if k >=2
for i = 2:k
y(k, i) = y(k, i - 1) + (y(k, i - 1) - y(k - 1, i - 1)) / (Q(k - 1, i - 1) - 1);
end
if abs(y(k, k) - y(k - 1, k - 1)) < TOL
nflag = 1;
end
end
k = k + 1;
end
k = k - 1;
if nflag == 0
h = h / 2;
if h < hmin
disp('h小于hmin');
flag = 0;
end
else
W0 = y(k, k);
T0 = T0 + h;
n = n + 1;
t(n) = T0;
omega(n) = W0;
if T0 >= endpoiny_b
flag = 0;
elseif T0 + h > endpoiny_b
h = endpoiny_b - T0;
else
if k <= 3 && h < 0.5 * hmax
h = 2 * h;
end
end
end
end
end
|
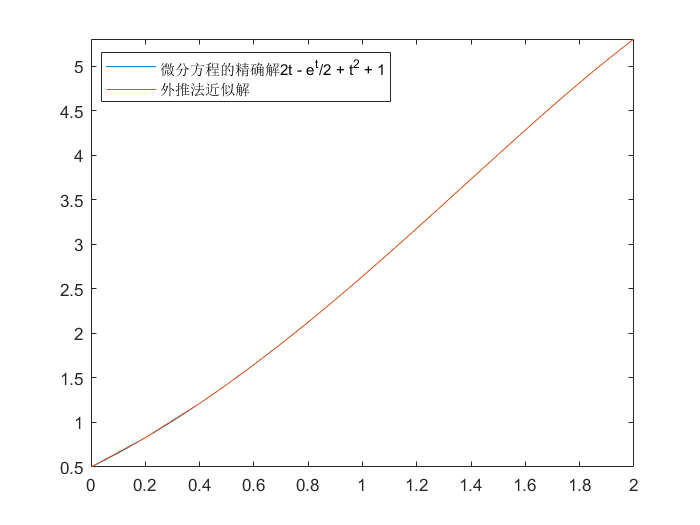
例如:
1
2
3
4
5
6
7
8
| >> y = dsolve('Dy - y + t^2 - 1 = 0', 'y(0)=0.5', 't')
>> fplot(y,[0, 2])
>> hold on
>> F = @(t, y)y - t^2 + 1
>> [t, u] = Extrapolation(F, 0.5, 0.000000000000001, 0.2, 0.001, 0, 2)
>> plot(t, u);
>> legend('微分方程的精确解2t - e^t/2 + t^2 + 1', '外推法近似解')
|

高阶方程与微分方程组
微分方程组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| function [t, omega] = Runge_Kutta_Equations(A, f, N, y_0, endpoint_a, endpoint_b)
h = (endpoint_b - endpoint_a) / N;
t(1) = endpoint_a;
omega(1, :) = y_0;
for i = 1:N
k1 = h * fun(f(t(i)), omega(i, :), A);
k2 = h * fun(f(t(i) + h / 2), omega(i, :) + 0.5 * k1, A);
k3 = h * fun(f(t(i) + h / 2), omega(i, :) + 0.5 * k2, A);
k4 = h * fun(f(t(i) + h), omega(i, :) + k3, A);
omega(i + 1, :) = omega(i, :) + (k1 +2 * k2 + 2 * k3 + k4) / 6;
t(i + 1) = endpoint_a + i * h;
end
end
function fx = fun(f, w, A)
[m, n] = size(A);
if n == length(w) && n == length(rot90(f))
fx = rot90(f + mtimes(A, w'));
else
disp('输入错误');
end
end
|
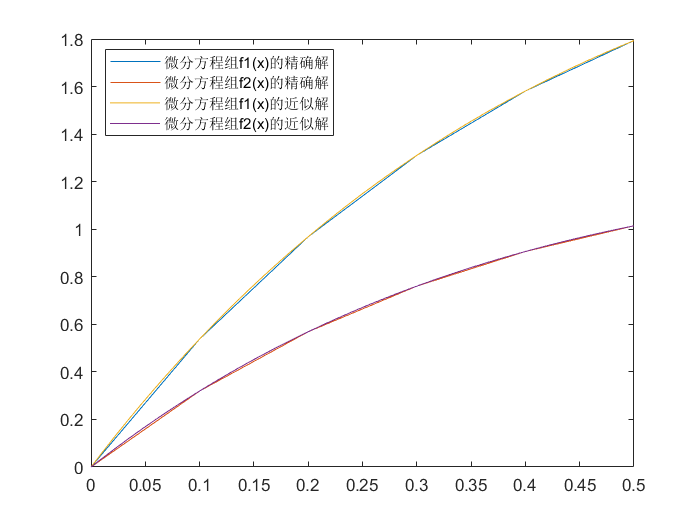
例如:
⎩⎨⎧x(t)=−4x+3y+6y(t)=−2.4x+1.6y+3.6x(0)=0,y(0)=0
通解为:
{x(t)=−3.375e−2t+1.875e−0.4t+1.5y(t)=−2.25e−2t+2.25e−0.4t
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| >> syms f1(x) f2(x)
>> f1(x) = 6
>> f2(x) = 3.6
>> A = [-4 3; -2.4 1.6]
>> f(x) = [f1(x); f2(x)]
>> y_0 = [0, 0]
>> [t, omega] = Runge_Kutta_Equations(A, f, 5, y_0, 0, 0.5)
>> plot(t, omega(:, 1))
>> hold on
>> plot(t, omega(:, 2))
>> hold on
>> [x y] = dsolve('Dx=-4*x+3*y+6,Dy=-2.4*x+1.6*y+3.6', 'x(0)=0,y(0)=0')
>> fplot(x, [0, 0.5])
>> hold on
>> fplot(y, [0, 0.5])
>> legend('微分方程组f1(x)的精确解','微分方程组f2(x)的精确解','微分方程组f1(x)的近似解','微分方程组f2(x)的近似解')
|

高阶微分方程
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| function [t, omega] = Higher_Order_Differential_Equations(a, f, N, y_0, endpoint_a, endpoint_b)
m = length(a);
syms x;
for i = 1:m - 1
for j = 1:m
if j == i + 1
A(i, j) = 1;
else
A(i, j) = 0;
end
end
end
for j = 1:m
A(m, j) = -1 * a(m - j + 1);
if j ~= m
F(x) = [0, f(x)];
end
end
F = rot90(F);
h = (endpoint_b - endpoint_a) / N;
t(1) = endpoint_a;
omega(1, :) = y_0;
for i = 1:N
k1 = h * fun(F(t(i)), omega(i, :), A);
k2 = h * fun(F(t(i) + h / 2), omega(i, :) + 0.5 * k1, A);
k3 = h * fun(F(t(i) + h / 2), omega(i, :) + 0.5 * k2, A);
k4 = h * fun(F(t(i) + h), omega(i, :) + k3, A);
omega(i + 1, :) = omega(i, :) + (k1 +2 * k2 + 2 * k3 + k4) / 6;
t(i + 1) = endpoint_a + i * h;
end
end
function fx = fun(f, w, A)
[m, n] = size(A);
if n == length(w) && n == length(rot90(f))
fx = rot90(f + mtimes(A, w'));
else
disp('输入错误');
end
end
|
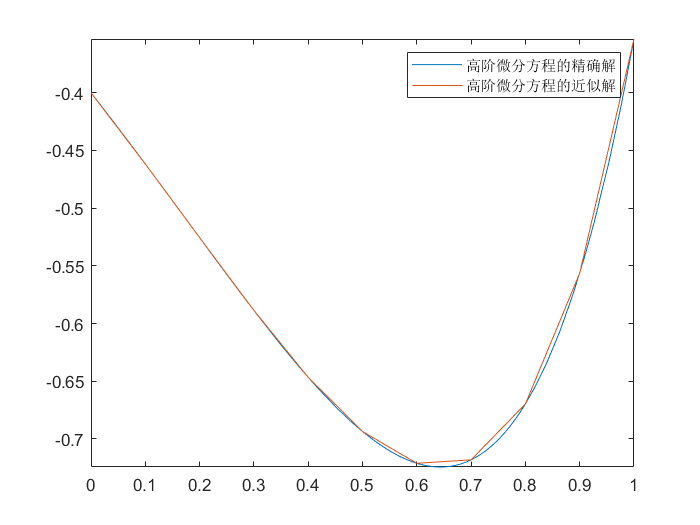
例如:
y′′−2y′+2y=e2tsinty(0)=−0.4,y′(0)=−0.6
通解:
y(t)=51e2t(sin(t)−2cos(t))
1
2
3
4
5
6
7
8
9
10
11
| >> y = dsolve('D2y-2*Dy+2*y=exp(2*x)*sin(x)', 'y(0)=-0.4,Dy(0)=-0.6', 'x')
>> fplot(y, [0, 1])
>> hold on
>> a = [-2 2]
>> syms f(x)
>> f(x) = exp(2 * x) * sin(x)
>> y_0 = [-0.4 -0.6]
>> [t, omega] = Higher_Order_Differential_Equations(a, f, 10, y_0, 0, 1)
>> plot(t, omega(:, 1))
>> legend('高阶微分方程的精确解','高阶微分方程的近似解')
|

刚性微分方程
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| function [t, omega] = Trapezoidal_Newton_Iteration(F, N, y_0, TOL, M, endpoint_a, endpoint_b)
syms t y;
f(t, y) = F(t, y);
dfy = diff(f, y);
dFy = matlabFunction(dfy);
h = (endpoint_b - endpoint_a) / N;
t(1) = endpoint_a;
omega(1) = y_0;
for i = 1:N
K1 = omega(i) + h / 2 * F(t(i), omega(i));
w0 = K1;
mark = 1;
flag = 0;
while flag == 0
omega(i + 1) = w0 - (w0 - h / 2 * F(t(i) + h, w0) - K1) / (1 - h / 2 * dFy(t(i) + h, w0));
if abs(omega(i + 1) - w0) < TOL
flag = 1;
else
mark = mark + 1;
w0 = omega(i + 1);
if mark > M
disp('超出最大迭代次数');
break;
end
end
end
t(i + 1) = endpoint_a + i * h;
end
end
|
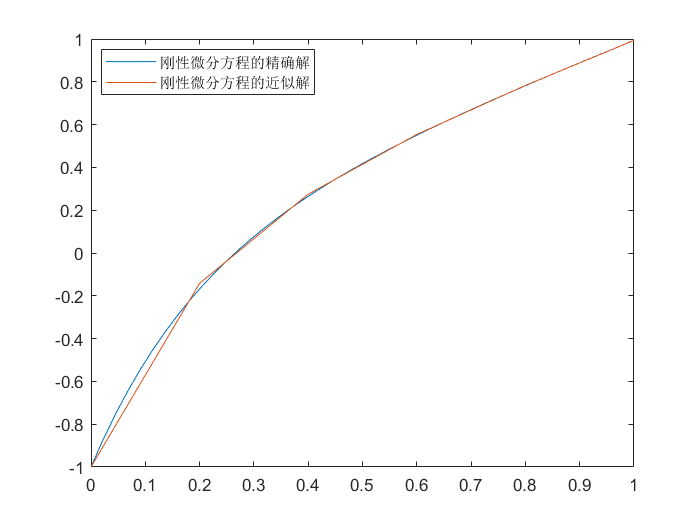
例如:
1
2
3
4
5
6
7
8
| >> y = dsolve('Dy=5*exp(5*t)*(y-t)^2+1', 'y(0)=-1')
>> fplot(y, [0, 1])
>> hold on
>> F = @(t, y)5 * exp(5 * t) * (y - t)^2 + 1
>> [t, omega] = Trapezoidal_Newton_Iteration(F, 5, -1, 0.000001, 10, 0, 1)
>> plot(t, omega)
>> legend('刚性微分方程的精确解','刚性微分方程的近似解')
|

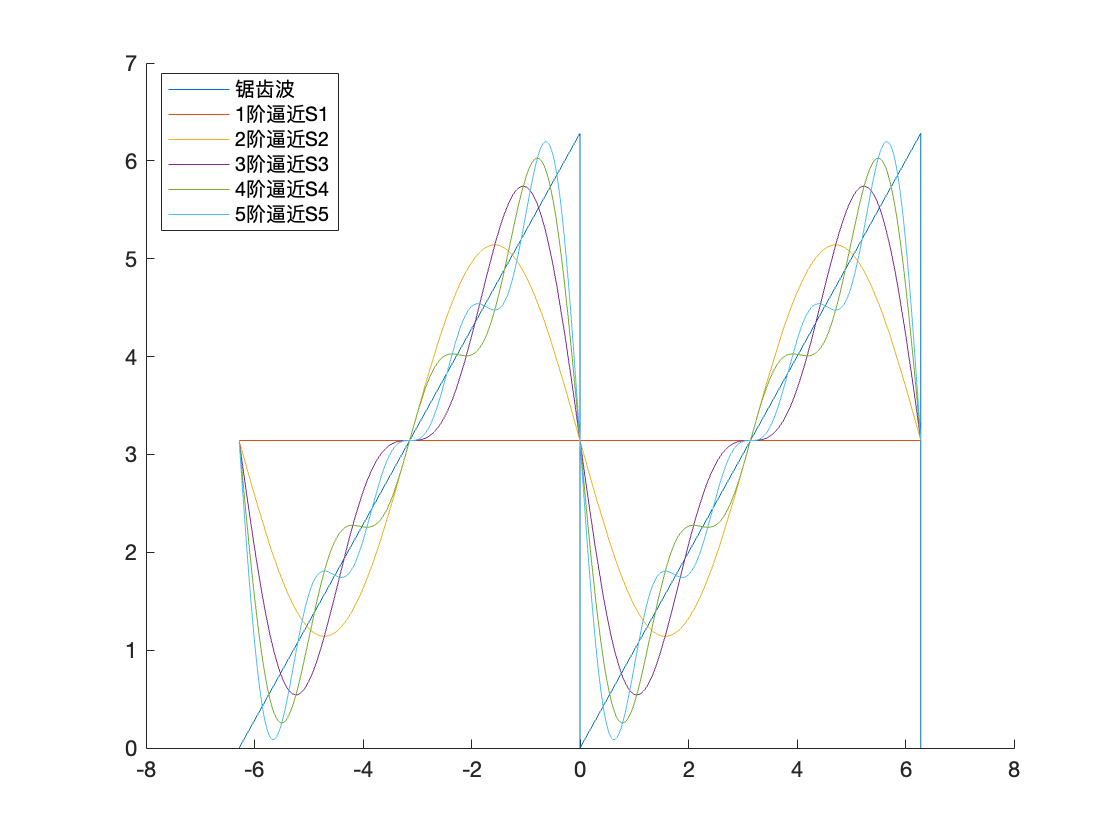
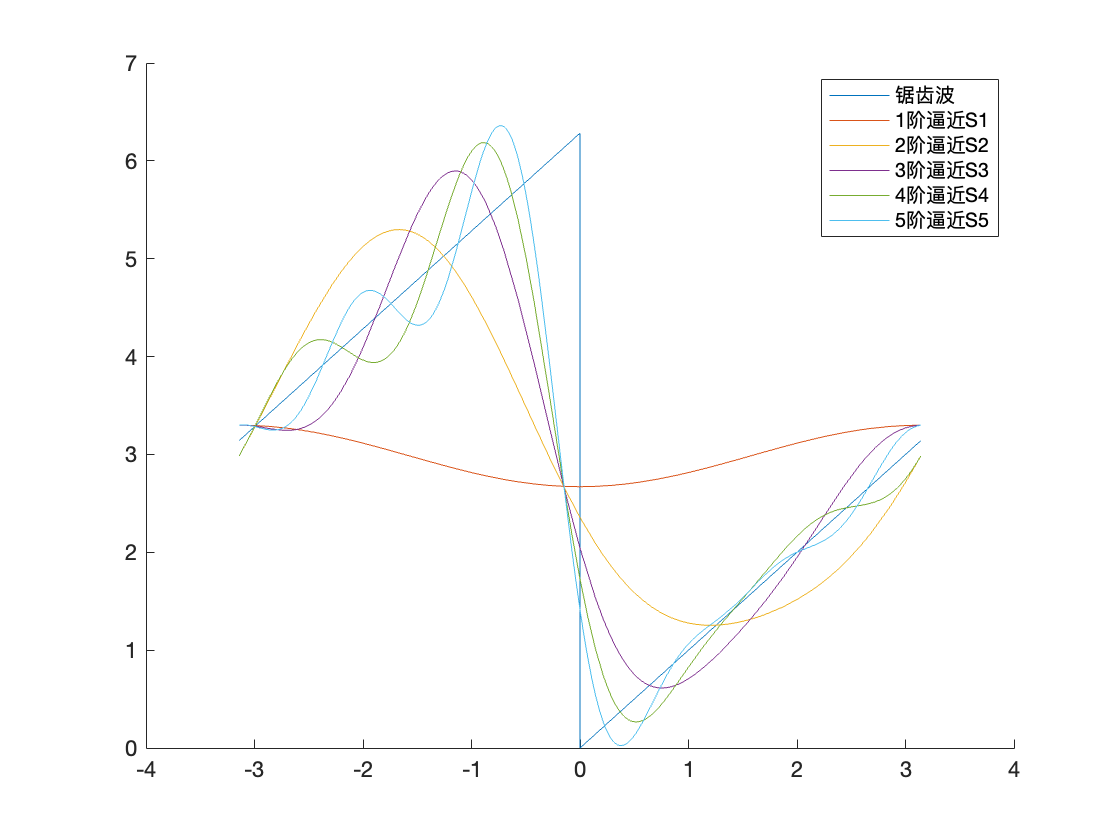
逼近论
多项式逼近
离散最小二乘法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| function P = Polynomial_Least_Squares(xx, yy, n)
syms x;
m = length(xx);
A = zeros(n + 1, n + 1);
b = zeros(n + 1, 1);
for i = 1:n + 1
for j = i:n + 1
sum_x_n = sum(xx .^ (i + j - 2));
A(i, j) = sum_x_n;
A(j, i) = sum_x_n;
end
sum_yx_n = sum(yy .* xx .^ (i - 1));
b(i) = sum_yx_n;
end
a = A \ b;
P = a(1);
for k = 1:n
P = P + a(k + 1) * x ^ k;
end
end
|
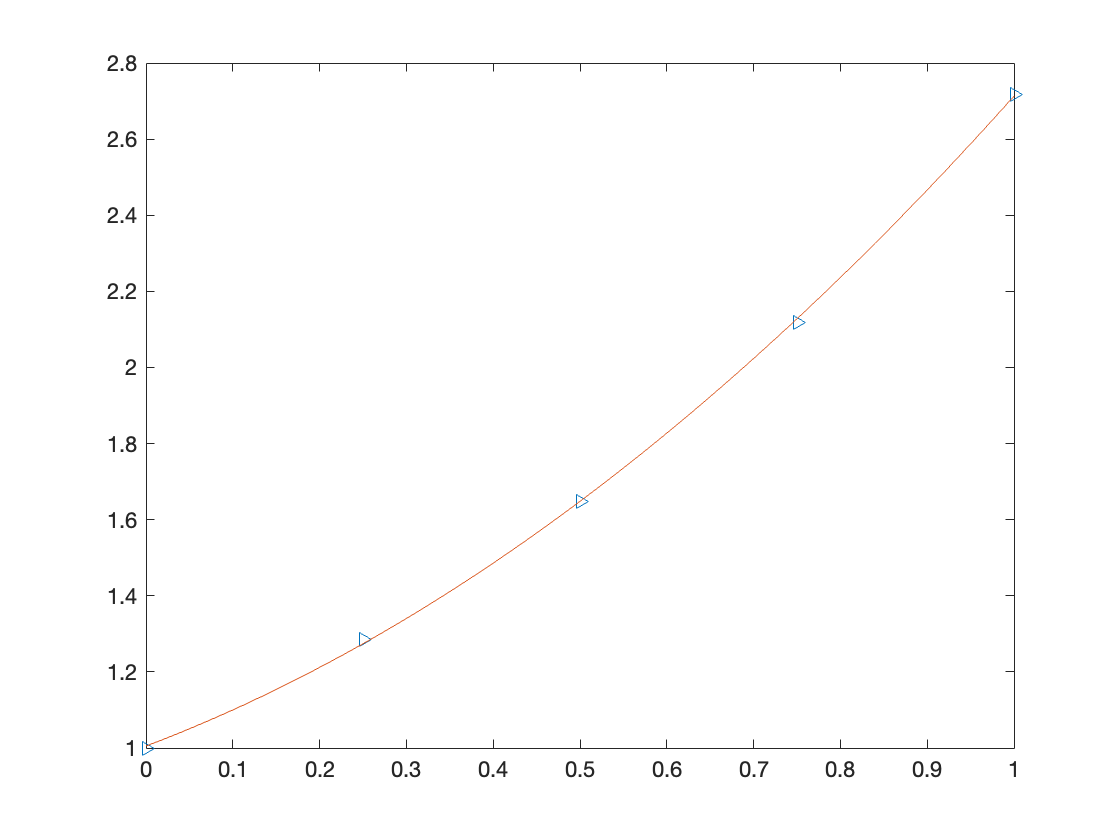
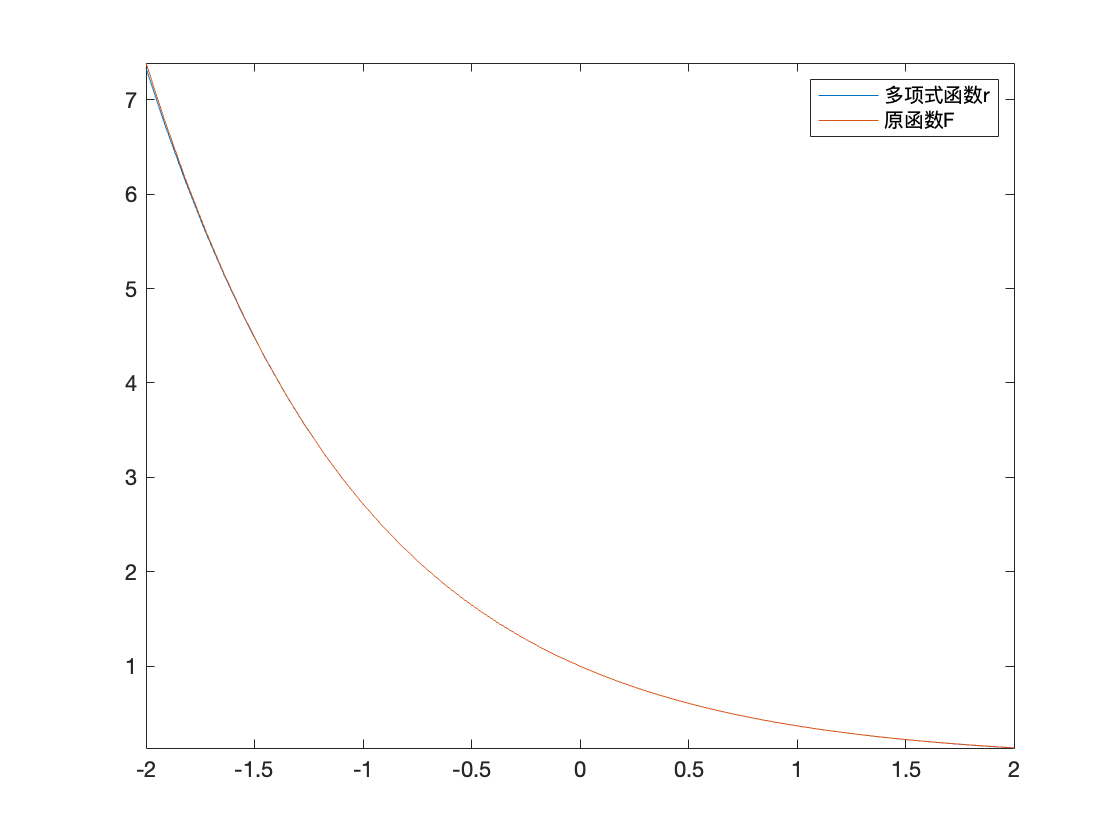
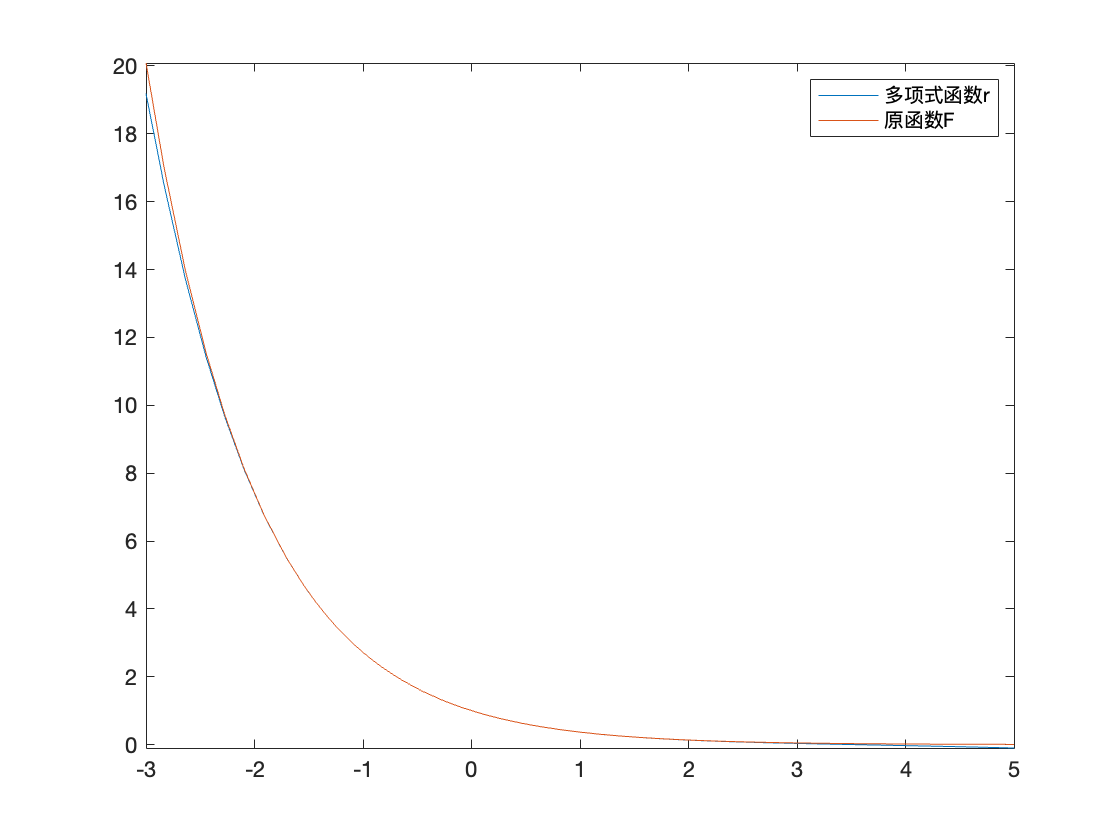
例如:
1
2
3
4
5
6
| >> xx = 0:0.25:1
>> yy = [1.0000, 1.2840, 1.6487, 2.1170, 2.7183]
>> plot(xx, yy, '>')
>> hold on
>> fplot(P, [0, 1])
|

连续最小二乘法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| function P = Polynomial_Least_Squares_Function(F, endpoint_a, endpoint_b, n)
syms x;
f = F(x);
A = zeros(n + 1, n + 1);
b = zeros(n + 1, 1);
for i = 1:n + 1
for j = i:n + 1
A(j, i) = (endpoint_b ^ (i + j - 1) - endpoint_a ^ (i + j - 1)) / (i + j - 1);
A(i, j) = A(j, i);
end
b(i) = int(f * x ^ (i - 1), x, endpoint_a, endpoint_b);
end
a = A \ b;
P = a(1);
for k = 1:n
P = P + a(k + 1) * x ^ k;
end
end
|
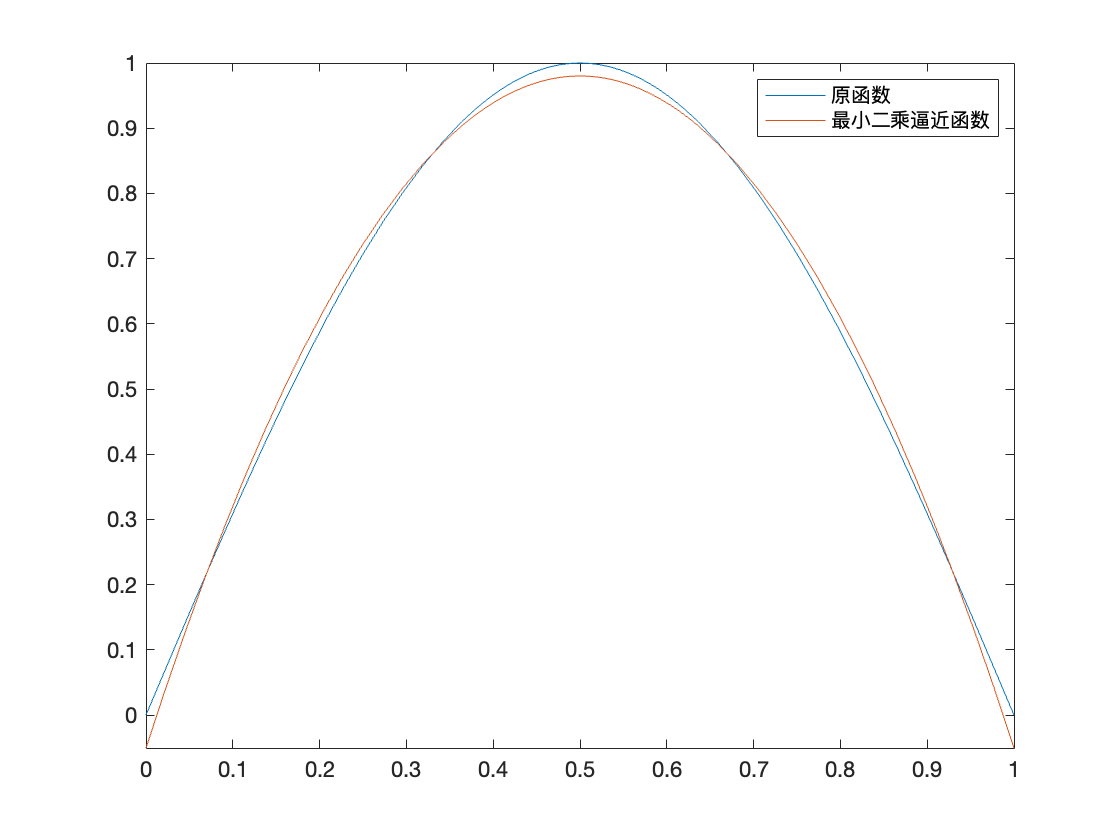
例如:
1
2
3
4
5
6
7
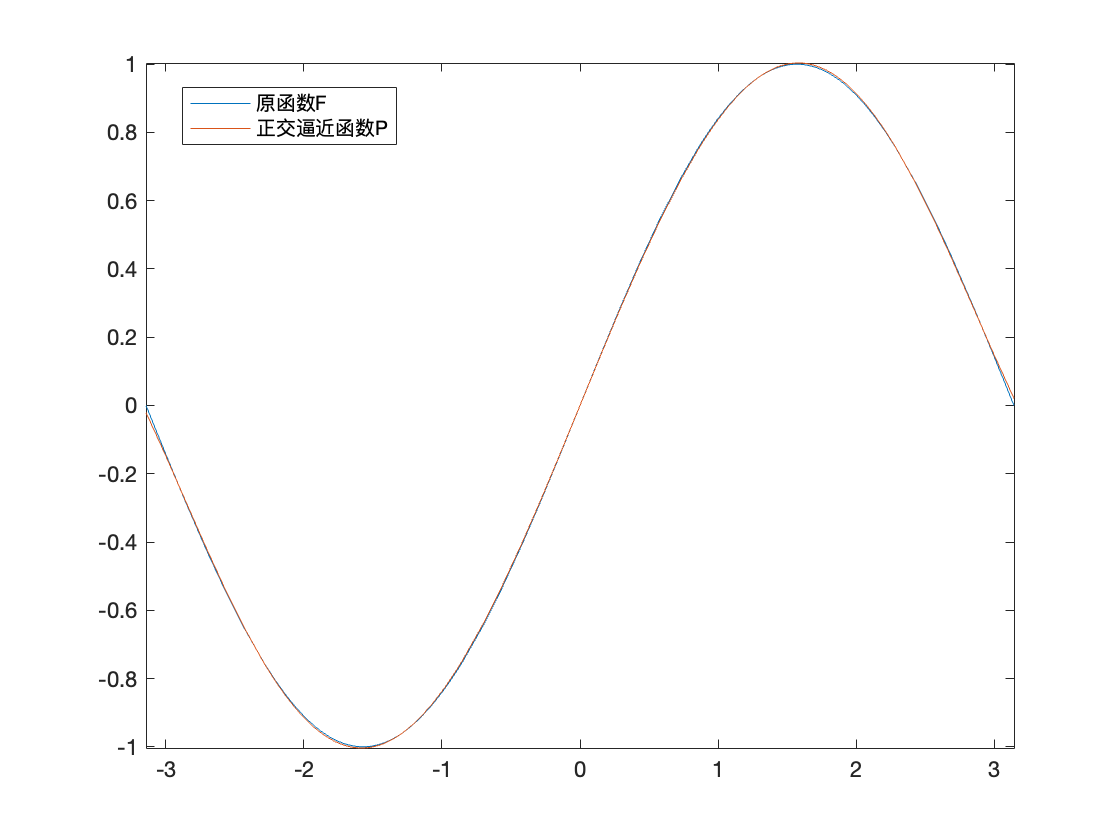
| >> F = @(x)sin(pi * x)
>> P = Polynomial_Least_Squares_Function(F, 0, 1, 2)
>> fplot(F, [0, 1])
>> hold on
>> fplot(P, [0, 1])
>> legend('原函数', '最小二乘逼近函数')
|

正交多项式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| function [Phi] = Gram_Schmidt_Orthogonal_Polynomials(Omega, endpoint_a, endpoint_b, n)
syms x;
omega = Omega(x);
Phi = sym('x', [1 n + 1]);
Phi(1) = 1;
B = int(x * omega * Phi(1) ^ 2, x, endpoint_a, endpoint_b) / int(omega * Phi(1) ^ 2, x, endpoint_a, endpoint_b);
Phi(2) = x - B;
for k = 3:n + 1
B = int(x * omega * Phi(k - 1) ^ 2, x, endpoint_a, endpoint_b) / int(omega * Phi(k - 1) ^ 2, x, endpoint_a, endpoint_b);
C = int(x * omega * Phi(k - 1) * Phi(k - 2), x, endpoint_a, endpoint_b) / int(omega * Phi(k - 2) ^ 2, x, endpoint_a, endpoint_b);
Phi(k) = simplify((x - B) * Phi(k - 1) - C * Phi(k - 2));
end
end
|
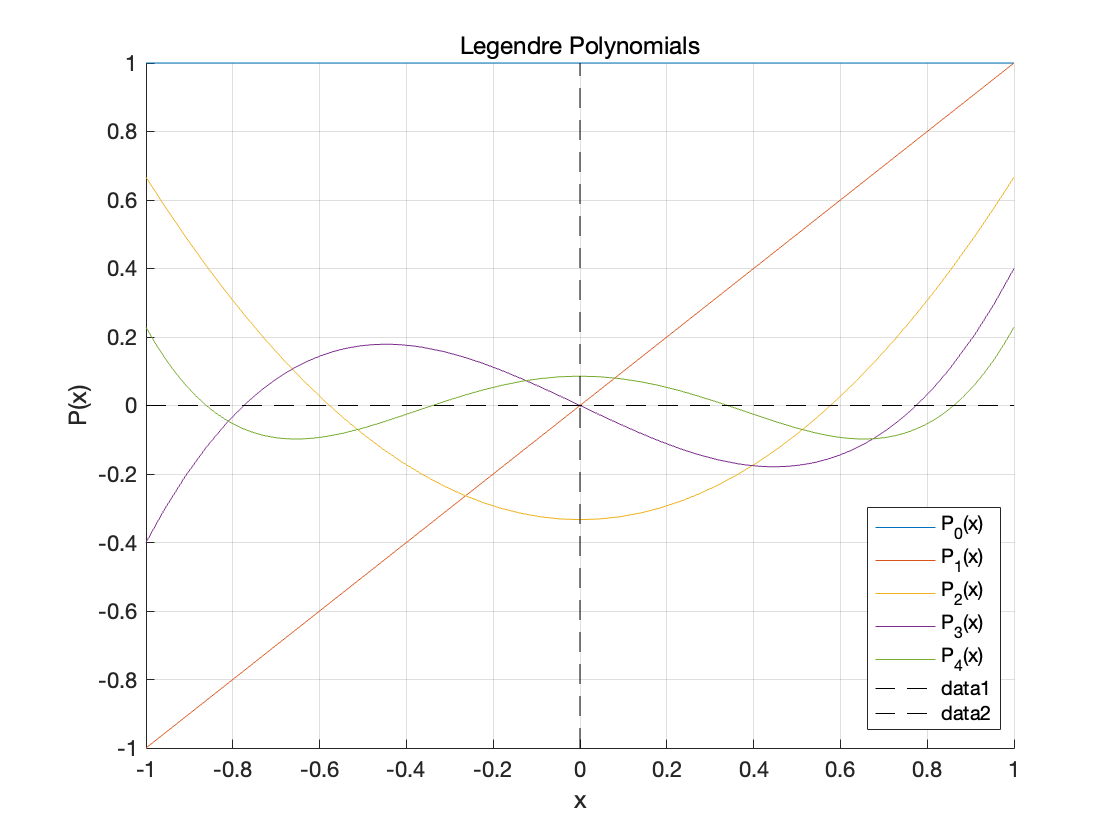
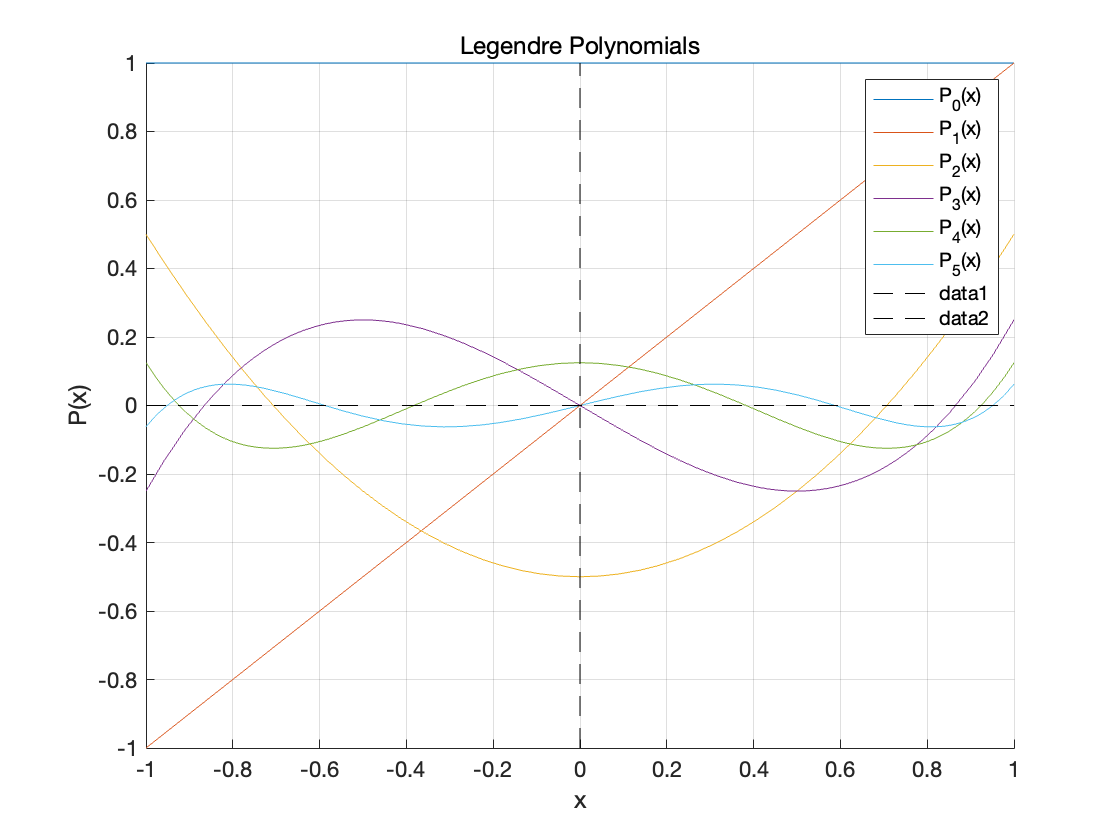
Legendre多项式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| >> Omega = @(x)1
>> [Phi] = Gram_Schmidt_Orthogonal_Polynomials(Omega, -1, 1, 5)
>> figure;
>> hold on;
>> for k = 1:length(Phi)
fplot(Phi(k), [-1, 1], 'DisplayName', sprintf('P_%d(x)', k-1));
end
>> legend('show');
>> grid on;
>> title('Legendre Polynomials');
>> xlabel('x');
>> ylabel('P(x)');
>> line([-1, 1], [0, 0], 'Color', 'k', 'LineStyle', '--');
>> line([0, 0], [min(ylim), max(ylim)], 'Color', 'k', 'LineStyle', '--');
>> hold off;
|

切比雪夫多项式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| function [Tn] = Chebyshev_Polynomial(endpoint_a, endpoint_b, n)
syms x;
Tn = sym('x', [1 n + 1]);
syms x_prime;
x_prime = ((endpoint_b - endpoint_a) * x + endpoint_a + endpoint_b) / 2;
Tn(1) = 1;
Tn(2) = simplify(x_prime);
Tn(3) = simplify(x_prime * Tn(2) - Tn(1) / 2);
for k = 4:n+1
Tn(k) = simplify(x_prime * Tn(k - 1) - Tn(k - 2) / 4);
end
end
|
例如:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| >> [Tn] = Chebyshev_Polynomial(-1, 1, 5)
>> figure;
>> hold on;
>> for k = 1:length(Tn)
fplot(Tn(k), [-1, 1], 'DisplayName', sprintf('P_%d(x)', k-1));
end
>> legend('show');
>> grid on;
>> title('Legendre Polynomials');
>> xlabel('x');
>> ylabel('P(x)');
>> line([-1, 1], [0, 0], 'Color', 'k', 'LineStyle', '--');
>> line([0, 0], [min(ylim), max(ylim)], 'Color', 'k', 'LineStyle', '--');
>> hold off;
|

正交多项式逼近
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| function P = Orthogonal_Polynomial_Least_Squares_Function(F, Omega, n, endpoint_a, endpoint_b)
syms x;
f = F(x);
omega = Omega(x);
omega = subs(omega, x, (2 * x - (endpoint_a + endpoint_b)) / (endpoint_b - endpoint_a));
[Phi] = Gram_Schmidt_Orthogonal_Polynomials(matlabFunction(omega), endpoint_a, endpoint_b, n);
a = sym(zeros(n + 1, 1));
for k = 1:n + 1
a(k) = integral(matlabFunction(omega * Phi(k) * f), endpoint_a, endpoint_b) / int(omega * Phi(k) ^ 2, x, endpoint_a, endpoint_b);
end
P = a(1);
for k = 1:n
P = P + a(k + 1) * Phi(k + 1);
end
P = simplify(P);
end
|
例如:
1
2
3
4
5
6
7
| >> F = @(x)sin(x)
>> Omega = @(x)1 / sqrt(1 - x ^ 2)
>> P = Orthogonal_Polynomial_Least_Squares_Function(F, Omega, 5, -3, 3)
>> fplot(F, [-pi, pi])
>> hold on
>> fplot(P, [-pi, pi])
|

多项式函数逼近
Pade逼近
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| function r = Pade_Approximation(F, numerator_n, denominator_m)
N = denominator_m + numerator_n;
syms x;
f = F(x);
maclaurin_series = taylor(f, x, 'Order', N + 1);
[coeffs_list, terms] = coeffs(maclaurin_series, x);
coeffs_list_reversed = fliplr(coeffs_list);
A = zeros(N, N);
b = zeros(N, 1);
for i = 1:N
for k = 1:i
if i - k + 1 <= denominator_m
A(i, i - k + 1) = coeffs_list_reversed(k);
end
end
if i <= numerator_n
A(i, denominator_m + i) = -1;
end
b(i) = -coeffs_list_reversed(i + 1);
end
pq = A \ b;
p = coeffs_list_reversed(1);
for k = 1:numerator_n;
p = p + x ^ k * pq(denominator_m + k);
end
q = 1;
for k = 1:denominator_m
q = q + x ^ k * pq(k);
end
r = simplify(p / q);
end
|
例如:
1
2
3
4
5
6
7
| >> F = @(x)exp(-x)
>> r = Pade_Approximation(F, 3, 2)
>> fplot(r, [-2, 2])
>> hold on
>> fplot(F, [-2, 2])
>> legend('多项式函数r', '原函数F')
|

切比雪夫多项式逼近
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
| function r = Chebyshev_Rational_Approximation(F, numerator_n, denominator_m)
N = denominator_m + numerator_n;
[Tn] = Chebyshev_Polynomial(-1, 1, N);
syms theta;
a = zeros(N + 1, 1);
a(1) = 1 / pi * int(F(cos(theta)), theta, 0, pi);
for k = 1:N
a(k + 1) = 2 / pi * int(F(cos(theta)) * cos(k * theta), theta, 0, pi);
end
A = zeros(N + 1, N + 1);
b = zeros(N + 1, 1);
for i = 1:N + 1
for j = 1:denominator_m
if i ~= 1
A(i, j) = 0;
if (1 <= i - j) && (i - j <= N + 1)
A(i, j) = A(i, j) + a(i - j);
end
if (1 <= i + j) && (i + j <= N + 1)
A(i, j) = A(i, j) + a(i + j);
end
if (-1 <= j - i) && (j - i <= N - 1)
A(i, j) = A(i, j) + a(j - i + 2);
end
else
A(i, j) = a(j + 1) / 2;
end
end
if i == 1
A(i, denominator_m + i) = -1;
elseif i <= numerator_n + 1
A(i, denominator_m + i) = -2;
end
if i ~= 1
b(i) = -2 * a(i);
else
b(i) = -a(i);
end
end
pq = A \ b;
p = pq(denominator_m + 1);
for k = 1:numerator_n
p = p + 2 ^ (k - 1) * Tn(k + 1) * pq(denominator_m + k + 1);
end
q = 1;
for k = 1:denominator_m
q = q + 2 ^ (k - 1) * Tn(k + 1) * pq(k);
end
r = simplify(p / q);
end
|
例如:
1
2
3
4
5
6
7
| >> F = @(x)exp(-x)
>> r = Chebyshev_Rational_Approximation(F, 3, 2)
>> fplot(r, [-3, 5])
>> hold on
>> fplot(F, [-3, 5])
>> legend('多项式函数r', '原函数F')
|

三角多项式逼近
连续函数逼近
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| function S = Trigonometric_Polynomial_Approximation(F, n)
syms x;
f = F(x);
a = zeros(n + 1, 1);
b = zeros(n, 1);
for k = 0:n
a(k + 1) = int(f * cos(k * x), x, -pi, pi) / pi;
end
for k = 1:n - 1
b(k) = int(f * sin(k * x), x, -pi, pi) / pi;
end
S = a(1) / 2;
for k = 1:n - 1
S = S + a(k + 1) * cos(k * x) + b(k) * sin(k * x);
end
S = S + a(n + 1) * cos(n * x);
end
|
例如:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| >> sawtoothWave = @(x) mod(x, 2 * pi);
>> S1 = Trigonometric_Polynomial_Approximation(sawtoothWave, 1)
>> S2 = Trigonometric_Polynomial_Approximation(sawtoothWave, 2)
>> S3 = Trigonometric_Polynomial_Approximation(sawtoothWave, 3)
>> S4 = Trigonometric_Polynomial_Approximation(sawtoothWave, 4)
>> S5 = Trigonometric_Polynomial_Approximation(sawtoothWave, 5)
>> figure;
>> hold on;
>> fplot(sawtoothWave, [-2 * pi, 2 * pi]);
>> fplot(S1, [-2 * pi, 2 * pi]);
>> fplot(S2, [-2 * pi, 2 * pi]);
>> fplot(S3, [-2 * pi, 2 * pi]);
>> fplot(S4, [-2 * pi, 2 * pi]);
>> fplot(S5, [-2 * pi, 2 * pi]);
>> legend('锯齿波', '1阶逼近S1', '2阶逼近S2', '3阶逼近S3', '4阶逼近S4', '5阶逼近S5');
>> hold off;
|

离散点逼近
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| function S = Discrete_Trigonometric_Polynomial_Approximation(xx, yy, n)
m = length(yy);
syms x;
a = zeros(n + 1, 1);
b = zeros(n, 1);
for k = 0:n
a(k + 1) = (2/m) * sum(yy .* cos(k * xx));
end
for k = 1:n - 1
b(k) = (2/m) * sum(yy .* sin(k * xx));
end
S = a(1) / 2;
for k = 1:n - 1
S = S + a(k + 1) * cos(k * x) + b(k) * sin(k * x);
end
S = S + a(n + 1) * cos(n * x);
end
|
例如:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| >> sawtoothWave = @(x) mod(x, 2 * pi);
>> m = 20
>> xx = linspace(-pi, (1 - 2 / m) * pi, m)
>> yy = sawtoothWave(xx)
>> S1 = Discrete_Trigonometric_Polynomial_Approximation(xx, yy, 1)
>> S2 = Discrete_Trigonometric_Polynomial_Approximation(xx, yy, 2)
>> S3 = Discrete_Trigonometric_Polynomial_Approximation(xx, yy, 3)
>> S4 = Discrete_Trigonometric_Polynomial_Approximation(xx, yy, 4)
>> S5 = Discrete_Trigonometric_Polynomial_Approximation(xx, yy, 5)
>> figure; % Create a new figure
>> hold on; % Hold the current plot
>> fplot(sawtoothWave, [-pi, pi]);
>> fplot(S1, [-pi, pi]);
>> fplot(S2, [-pi, pi]);
>> fplot(S3, [-pi, pi]);
>> fplot(S4, [-pi, pi]);
>> fplot(S5, [-pi, pi]);
>> legend('锯齿波', '1阶逼近S1', '2阶逼近S2', '3阶逼近S3', '4阶逼近S4', '5阶逼近S5');
>> hold off; % Release the hold
|

快速傅立叶变换
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| function y = FFT(a)
n = length(a);
y = zeros(n, 1);
if n ~= 2 ^ nextpow2(n)
error('输入数组的长度非2的整数次幂');
end
if n == 1
y(1) = a(1);
return;
end
a_odd = a(1:2:end);
a_even = a(2:2:end);
y_odd = FFT(a_odd);
y_even = FFT(a_even);
for k = 1:n / 2
omega_k = exp(2 * pi * 1i * (k - 1) / n);
y(k) = y_odd(k) + omega_k * y_even(k);
y(k + n / 2) = y_odd(k) - omega_k * y_even(k);
end
end
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| function a = DFT(y)
N = length(y);
a = recursiveDFT(y) / N;
end
function a = recursiveDFT(y)
n = length(y);
a = zeros(n, 1);
if n ~= 2 ^ nextpow2(n)
error('输入数组的长度非2的整数次幂');
end
if n == 1
a(1) = y(1);
return;
end
y_odd = y(1:2:end);
y_even = y(2:2:end);
a_odd = recursiveDFT(y_odd);
a_even = recursiveDFT(y_even);
for j = 1:n / 2
omega_j = exp(-2 * pi * 1i * (j - 1) / n);
a(j) = (a_odd(j) + omega_j * a_even(j));
a(j + n / 2) = (a_odd(j) - omega_j * a_even(j));
end
end
|