前言

学习粒子滤波，主要是为了大创的IVR，系统的学习了一遍之后，发现大创也就如此，之前的一些疑惑都统统扫除，感觉自己也能对别人的论文挥斥方遒一样(bushi)

视频链接

# 贝叶斯公式

离散：

P(X=x∣Y=y)=P(Y=y∣X=x)P(X=x)P(Y=y)P(X=x|Y=y) = \frac{P(Y=y|X=x)P(X=x)}{P(Y=y)}

连续：

P(X<x∣Y=y)=P(Y=y∣X<x)P(X<x)P(Y=y)P(X<x|Y=y) = \frac{P(Y=y|X<x)P(X<x)}{P(Y=y)}

定理：

fX(x)∼N(u1,σ12)，fY∣X(y∣x)∼N(u2,σ22)fX∣Y(x∣y)∼N(σ12σ12+σ22u2+σ22σ12+σ22u1,σ12σ22σ12+σ22)f_{X}(x) \sim N(u_1,\sigma_1 ^2)，f_{Y|X}(y|x) \sim N(u_2,\sigma_2 ^2)\\ f_{X|Y}(x|y) \sim N(\frac{\sigma_1 ^2}{\sigma_1 ^2 + \sigma_2 ^2}u_2 + \frac{\sigma_2 ^2}{\sigma_1 ^2 + \sigma_2 ^2}u_1 ,\frac{\sigma_1 ^2 \sigma_2 ^2}{\sigma_1 ^2 + \sigma_2 ^2})

分析：

若σ12≫σ22,fX∣Y(x∣y)∼N(σ12σ12+σ22u2+σ22σ12+σ22u1,σ12σ22σ12+σ22)≈N(u2,σ22)(倾向观测值)若σ12≪σ22,fX∣Y(x∣y)∼N(σ12σ12+σ22u2+σ22σ12+σ22u1,σ12σ22σ12+σ22)≈N(u1,σ21)(倾向预测值)\begin{align*} 若\sigma_1 ^2 \gg \sigma_2 ^2,f_{X|Y}(x|y) \sim N(\frac{\sigma_1 ^2}{\sigma_1 ^2 + \sigma_2 ^2}u_2 + \frac{\sigma_2 ^2}{\sigma_1 ^2 + \sigma_2 ^2}u_1 ,\frac{\sigma_1 ^2 \sigma_2 ^2}{\sigma_1 ^2 + \sigma_2 ^2})\approx N(u_2,\sigma_2 ^2) \qquad (倾向观测值)\\ 若\sigma_1 ^2 \ll \sigma_2 ^2,f_{X|Y}(x|y) \sim N(\frac{\sigma_1 ^2}{\sigma_1 ^2 + \sigma_2 ^2}u_2 + \frac{\sigma_2 ^2}{\sigma_1 ^2 + \sigma_2 ^2}u_1 ,\frac{\sigma_1 ^2 \sigma_2 ^2}{\sigma_1 ^2 + \sigma_2 ^2})\approx N(u_1,\sigma_2 ^1) \qquad (倾向预测值) \end{align*}

狄拉克函数

δ(x)={0,x≠0∞,x=0满足∫−∞+∞δ(x)dx=1\begin{equation} \delta (x)=\left\{ \begin{aligned} 0 \qquad,& x \neq 0 \\ \infty \qquad,& x = 0 \\ \end{aligned} \right. \end{equation} \qquad 满足 \int_{-\infty}^{+\infty} \delta (x) dx = 1

实质上δ(x)\delta (x)为必然事件的概率密度

H(x)={1,x≥00,x<0则δ(x)=ddxH(x)\begin{equation} H (x)=\left\{ \begin{aligned} 1 \qquad,& x \ge 0 \\ 0 \qquad,& x < 0 \\ \end{aligned} \right. \end{equation} \qquad 则 \delta(x)=\frac{d}{dx}H(x)

定理：

∫−∞+∞f(x)δ(x)dx=f(0)\int_{-\infty}^{+\infty} f(x)\delta (x) dx = f(0)

推论：

∫abδ(x)dx=1a<0<b∫abf(x)δ(x)dx=f(0)a<0<b∫cdf(x)δ(x−a)dx=f(a)c<a<d\begin{align*} &\int_{a}^{b} \delta (x) dx = 1 \qquad &a<0<b \\ &\int_{a}^{b} f(x)\delta (x) dx = f(0) \qquad &a<0<b \\ &\int_{c}^{d} f(x)\delta (x - a) dx = f(a) \qquad &c<a<d \\ \end{align*}

贝叶斯滤波算法

状态方程:Xk=f(Xk−1)+Qk观测方程:Yk=H(Xk)+Rk\begin{align*} 状态方程:&\qquad X_k = f(X_{k-1}) + Q_k\\ 观测方程:&\qquad Y_k = H(X_k) + R_k \\ \end{align*}

算法：

初值:X0∼f0(x)预测步:fk−(x)=∫−∞+∞fQk(x−f(v))fk−1+(v)dv更新步:fk+(x)=ηkfRk(yk−h(x))fk−(x),ηk=[∫−∞+∞fRk(yk−h(x))fk−(x)]−1期望估计值:x^k+=∫−∞+∞xfk+(x)dx\begin{align*} 初值:&\qquad X_0 \sim f_0(x) \\ 预测步:& \qquad f_k ^{-}(x) = \int_{-\infty}^{+\infty} f_{Q_k}(x-f(v))f_{k-1}^{+}(v) dv \\ 更新步:& \qquad f_k^{+}(x) = \eta_k f_{R_k}(y_k-h(x))f_k^{-}(x) \qquad ,\eta_k=[\int_{-\infty}^{+\infty} f_{R_k}(y_k-h(x))f_k^{-}(x)]^{-1} \\ 期望估计值:& \qquad \hat{x}_k^{+} = \int_{-\infty}^{+\infty} xf_k^{+}(x)dx \\ \end{align*}

缺点：难以处理无穷积分

对策：

  • 对状态方程、观测方程做假设

f(xk−1),h(xk)为线性函数⇒Kalman Filter卡尔曼滤波Qk,Rk为正态分布f(xk−1),h(xk)为非线性函数⇒Extend Kalman Filter拓展卡尔曼滤波Qk,Rk为正态分布\begin{align*} f(x_{k-1}),h(x_k)为线性函数& \\ &\Rightarrow \quad Kalman\ Filter \quad卡尔曼滤波 \\ Q_k,R_k为正态分布& \\ \\ f(x_{k-1}),h(x_k)为非线性函数& \\ &\Rightarrow \quad Extend\ Kalman\ Filter \quad 拓展卡尔曼滤波 \\ Q_k,R_k为正态分布& \\ \end{align*}

  • 处理无穷积分 高斯积分 ⇒\Rightarrow粒子滤波

  • 处理分布函数 无迹卡尔曼滤波

速度 精度 稳定性
EKF 快 差 较稳定
PK 慢 高 较稳定
UKF 较快 较高 很不稳定，易崩溃(维度越高越不稳定)

卡尔曼滤波

条件：

f(xk−1)=FXk−1h(xk)=hXk假设为线性函数f(x_{k-1}) = F X_{k-1} \quad h(x_k) = h X_k \qquad 假设为线性函数

fQ(x)=12πQe−x22RfR(x)=12πRe−x22Rf_Q(x) = \frac{1}{\sqrt{2\pi Q}}e^{-\frac{x^2}{2R}} \quad f_R(x) = \frac{1}{\sqrt{2\pi R}}e^{-\frac{x^2}{2R}}

设Xk−1∼N(uk−1+,σk−1+)Q∼N(0,Q)R∼N(0,R)设X_{k-1} \sim N(u_{k-1}^{+} , \sigma_{k-1}^{+}) \qquad Q \sim N(0,Q) \qquad R \sim N(0,R)

算法：

uk−=Fuk−1+σk−=F2σk−1++QK=hσk−h2σk−+Ruk+=uk−=K(yk−huk−)σk+=(1−Kh)σk−u_k^{-}=F u_{k-1}^+ \qquad\sigma_k^{-} = F^2 \sigma_{k-1}^{+} + Q \qquad K = \frac{h\sigma_k^{-}}{h^2\sigma_k^{-} + R} \\ u_k^{+} = u_k^{-} = K(y_k - hu_k^{-}) \qquad \sigma_k^{+} = (1 - Kh)\sigma_k^{-}

分析：K=hh2−R/σk−K=\frac{h}{h^2 - R/\sigma _k ^{-}}

若R≫σk−,K→0,uk+=uk−+K(yk−huk−)→uk−(倾向预测值)若R≪σk−,K→1h,uk+=uk−+K(yk−huk−)→ykh(倾向预测值)\begin{align*} &若R \gg \sigma_k ^{-}, K \rightarrow 0 , u_k^{+} = u_k^{-} + K(y_k - hu_k^{-}) \rightarrow u_k^{-} \qquad &(倾向预测值)\\ &若R \ll \sigma_k ^{-}, K \rightarrow \frac{1}{h} , u_k^{+} = u_k^{-} + K(y_k - hu_k^{-}) \rightarrow \frac{y_k}{h} \qquad &(倾向预测值) \end{align*}

矩阵形式的卡尔曼滤波

uk⇒u⃗kσk⇒∑kF、H、Q、R皆为矩阵u_k \Rightarrow \vec{u}_k \qquad \sigma_k \Rightarrow \sum\nolimits_{k} \\ F、H、Q、R皆为矩阵

算法：

u⃗k−=Fu⃗k−1−∑k−=F∑k−1−FT+QK=∑k−HT(H∑k−HT+R)−1u⃗k+=u⃗k−+K(y⃗k−Hu⃗k−)∑k+=(I−KH)∑k−\begin{align*} \vec{u}_k^{-} &= F \vec{u}_{k - 1}^{-} \\ \sum\nolimits_{k}^{-} &= F\sum\nolimits_{k - 1}^{-} F^{T} + Q \\ K &= \sum\nolimits_{k}^{-} H^{T}(H\sum\nolimits_{k}^{-}H^{T} + R)^{-1} \\ \vec{u}_k^{+} &= \vec{u}_k^{-} + K(\vec{y}_k - H\vec{u}_k^{-}) \\ \sum\nolimits_{k}^{+} &= (I - KH)\sum\nolimits_{k}^{-}\\ \end{align*}

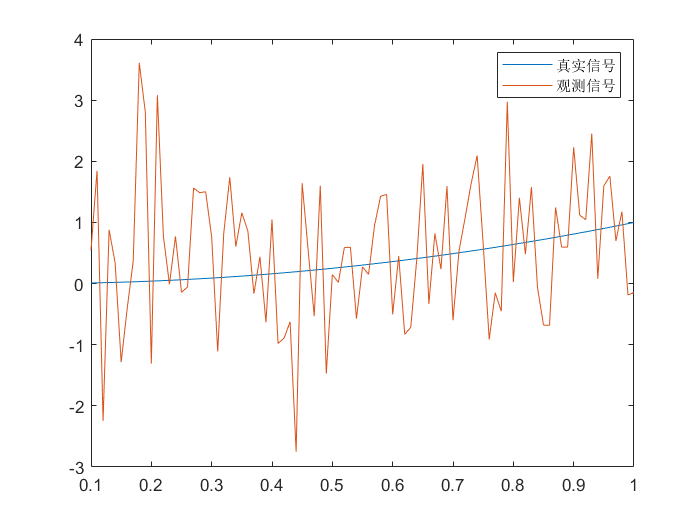
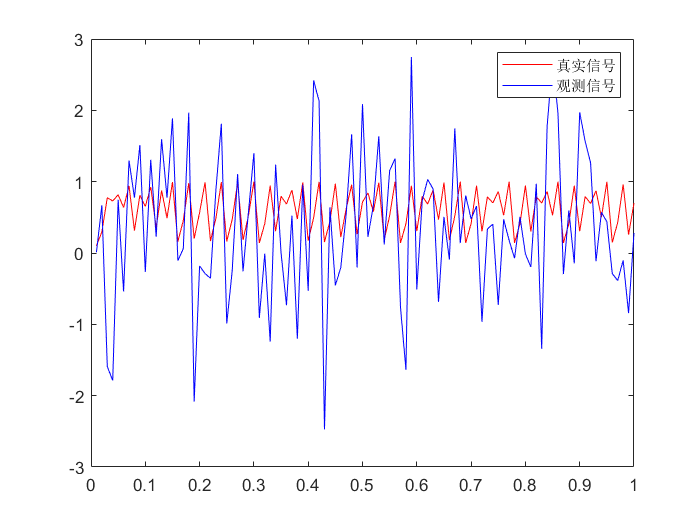
生成高斯噪声信号：

x=t2x=t^2 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
%生成一段时间t
t = 0.1:0.01:1;
L = length(t);

%生成真实信号x，以及观测信号y

%初始化
x = zeros(1, L);
y = x;

%生成信号，设x=t^2
for i = 1:L

    x(i) = t(i)^2;
    y(i) = x(i) + normrnd(0, 1);

end

%输出生成的信号
plot(t, x, t, y);
legend('真实信号','观测信号');

高斯噪声_卡尔曼滤波

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
function Xplus = Kalman_Filter(y, F, Q, H, R, Xplus_0, Pplus_0)

    L = length(y);
    n = length(F);

    %初始化X(k)plus
    Xplus = zeros(n, L);

    %初值
    Xplus(:, 1) = Xplus_0;
    Pplus = Pplus_0;

    for i = 2:L

        %预测步
        Xminus = F * Xplus(:, i - 1);
        Pminus = F * Pplus * F' + Q;

        %更新步
        K = (Pminus * H') * inv(H * Pminus * H' + R);
        Xplus(:, i) = Xminus + K * (y(i) - H * Xminus);
        Pplus = (eye(n) - K * H) * Pminus;

    end

end

简单模型：

Xk=Xk−1+QYk=Xk−1+RX_{k} = X_{k-1} + Q \\ Y_{k} = X_{k-1} + R 

1
2
3
4
5
6
7
8
9
10
11
12
>> F = 1;
>> H = 1;
>> Q = 1;
>> R = 1;
>> Xplus_0 = 0.01;
>> Pplus_0 = 0.01^2;

>> Xplus1 = Kalman_Filter(y, F, H, Q, R, Xplus_0, Pplus_0);

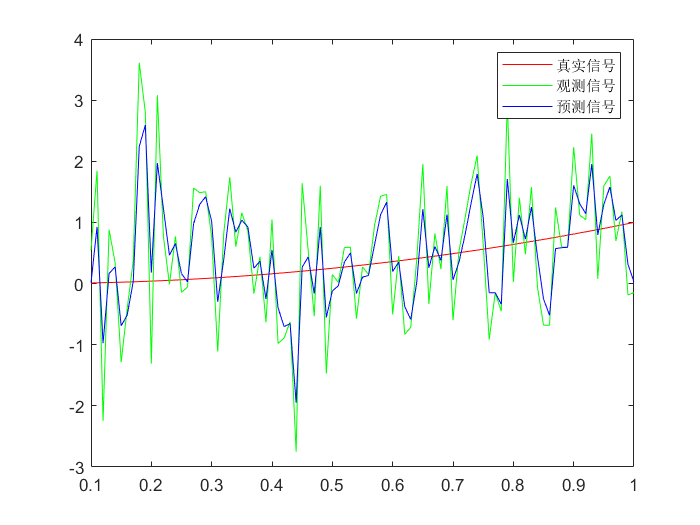
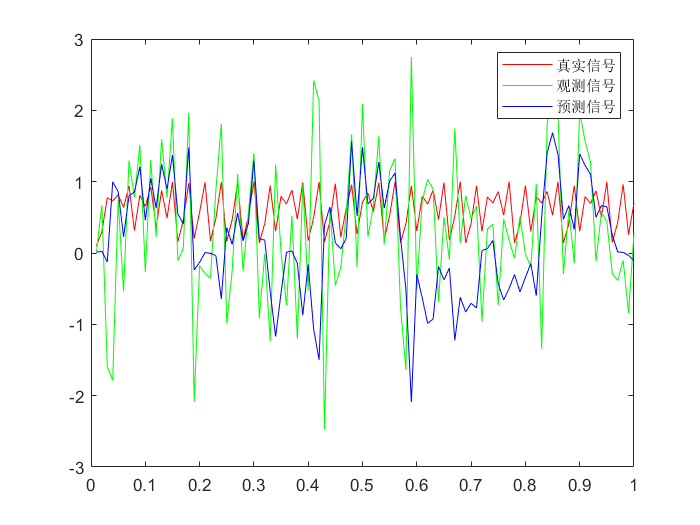
>> plot(t, x, 'r', t, y, 'g', t, Xplus1, 'b');
>> legend('真实信号', '观测信号', '预测信号');

卡尔曼滤波

预测方程优化：

Xk=Xk−1+Xk−1′dt+Xk−1′′(dt)22!Xk′=Xk−1′+Xk−1′dtXk′′=Xk−1′′dt\begin{align*} X_k &= X_{k-1} + X'_{k-1} dt + X''_{k-1} \frac{(dt)^2}{2 !} \\ X'_k &= X'_{k-1} + X'_{k-1} dt \\ X''_k &=X''_{k-1} dt \\ \end{align*} 

1
2
3
4
5
6
7
8
9
10
11
12
13
>> dt = t(2) - t(1);
>> F = [1, dt, 0.5 * dt^2; 0, 1, dt; 0, 0, 1];
>> H = [1, 0, 0];
>> Q = [1, 0, 0; 0, 0.01, 0; 0, 0, 0.0001];
>> R = 20;
>> Xplus_0 = [0.1^2, 0, 0];
>> Pplus_0 = [0.01, 0, 0; 0, 0.01, 0; 0, 0, 0.0001];

>> Xplus2 = Kalman_Filter(y, F, Q, H, R, Xplus_0, Pplus_0);

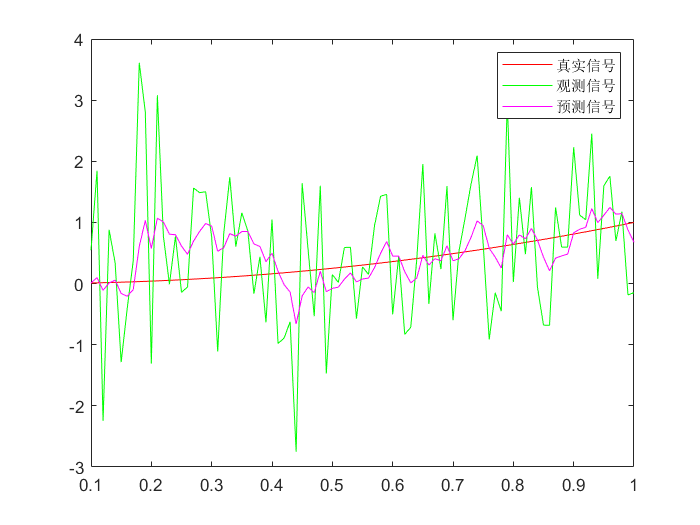
>> plot(t, x, 'r', t, y, 'g', t, Xplus2(1, :), 'm');
>> legend('真实信号', '观测信号', '预测信号');

卡尔曼滤波_改进

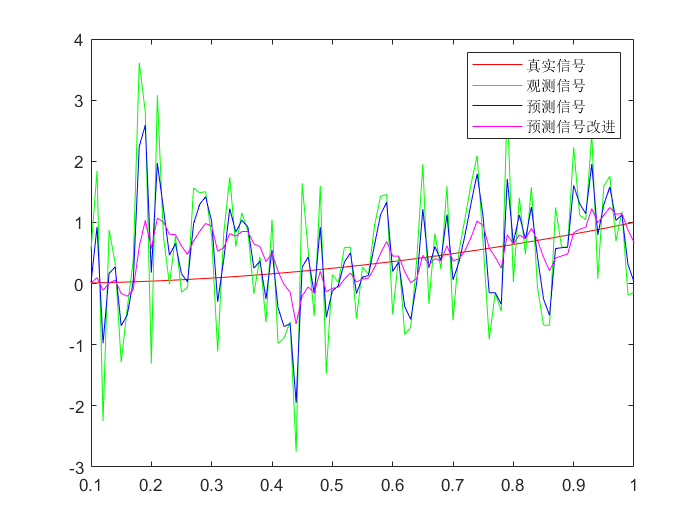
综合比较：

1
2
3
>> plot(t, x, 'r', t, y, 'g', t, Xplus1, 'b', t, Xplus2(1, :), 'm');
>> legend('真实信号', '观测信号', '预测信号', '预测信号改进');

卡尔曼滤波_比较

拓展卡尔曼滤波

条件：

f(xk−1) 与 h(xk)假设为非线性函数f(x_{k-1})\ 与\ h(x_k) \qquad 假设为非线性函数

对f(xk−1)f(x_{k-1})与h(xk)h(x_k)线性化

状态方程: Xk=f(Xk−1)+QkXk−1∼N(x^k−1+,Pk−1+)泰勒展开: f(xk−1)≈f(x^k−1+)+f′(x^k−1+)(Xk−1−x^k−1+)≈f′(x^k−1+)Xk−1+[f(x^k−1+)−f′(x^k−1+)x^k−1+]令A=f′(x^k−1+)B=f(x^k−1+)−f′(x^k−1+)x^k−1+预测方程: Xk=AXk−1+B+Qk观测方程: Yk=f(Xk)+RkXk∼N(x^k−,Pk−)泰勒展开: h(xk)≈h(x^k−)+h′(x^k−)(Xk−x^k−)≈h′(x^k−)Xk+[h(x^k−)−h′(x^k−)x^k−]令C=h′(x^k−)D=h(x^k−)−h′(x^k−)x^k−更新方程: Yk=CXk+D+Rk\begin{align*} 状态方程: \ &X_k = f(X_{k-1}) +Q_k \quad X_{k-1} \sim N(\hat{x}^{+}_{k-1},P^{+}_{k-1}) \\ 泰勒展开: \ &f(x_{k-1}) \approx f(\hat{x}^{+}_{k-1}) + f'(\hat{x}^{+}_{k-1})(X_{k-1}-\hat{x}^{+}_{k-1}) \approx f'(\hat{x}^{+}_{k-1})X_{k-1} + [f(\hat{x}^{+}_{k-1})-f'(\hat{x}^{+}_{k-1})\hat{x}^{+}_{k-1}] \\ 令\quad &A=f'(\hat{x}^{+}_{k-1})\quad B = f(\hat{x}^{+}_{k-1})-f'(\hat{x}^{+}_{k-1})\hat{x}^{+}_{k-1} \\ 预测方程:\ &X_k = AX_{k-1} + B +Q_k \\ \\ 观测方程: \ &Y_k = f(X_{k}) +R_k \quad X_{k} \sim N(\hat{x}^{-}_{k},P^{-}_{k}) \\ 泰勒展开: \ &h(x_{k}) \approx h(\hat{x}^{-}_{k}) + h'(\hat{x}^{-}_{k})(X_{k}-\hat{x}^{-}_{k}) \approx h'(\hat{x}^{-}_{k})X_{k} + [h(\hat{x}^{-}_{k}) - h'(\hat{x}^{-}_{k})\hat{x}^{-}_{k}] \\ 令\quad &C=h'(\hat{x}^{-}_{k})\quad D = h(\hat{x}^{-}_{k})-h'(\hat{x}^{-}_{k})\hat{x}^{-}_{k} \\ 更新方程:\ &Y_k = CX_{k} + D +R_k \end{align*}

算法：

Xk−1∼N(x^k−1+,pk−1+)预测步: A=f′(x^k−1+)x^k−=f(x^k−1+)Pk−=A2Pk−1++Q更新步: C=h′(x^k−)K=CPk−C2Pk−+Rx^k+=x^k−+K(yk−h(x^k−))Pk+=(1−KC)Pk−\begin{align*} &X_{k-1} \sim N(\hat{x}^{+}_{k-1},p^{+}_{k-1}) \\ 预测步:\ &A=f'(\hat{x}^{+}_{k-1}) \qquad \hat{x}^{-}_k = f(\hat{x}^{+}_{k-1}) \qquad P^{-}_{k} = A^2P^{+}_{k-1} + Q \\ 更新步:\ &C=h'(\hat{x}^{-}_k) \qquad K = \frac{CP^{-}_{k}}{C^2P^{-}_{k}+R} \qquad \hat{x}^{+}_k = \hat{x}^{-}_k +K(y_k - h(\hat{x}^{-}_k)) \qquad P^{+}_k = (1 - KC)P^{-}_k \\ \end{align*}

矩阵形式：

X⃗k−1∼N(x⃗^k−1+,∑k−1+)A=(∂f1∂xk−1(1)∂f1∂xk−1(2)⋯∂f1∂xk−1(n)⋮⋮⋱⋮∂fn∂xk−1(1)∂fn∂xk−1(2)⋯∂fn∂xk−1(n))x⃗k−=f(x⃗^k−1+)∑k−1−=A∑k−1+AT+QC=(∂h1∂xk(1)∂h1∂xk(2)⋯∂h1∂xk(n)⋮⋮⋱⋮∂hn∂xk(1)∂hn∂xk(2)⋯∂hn∂xk(n))K=∑k−CT(C∑k−CT+R)x⃗k+=x⃗k−+K(y⃗−h(x⃗k−))∑k+=(I−KC)∑k−\begin{align*} &\vec{X}_{k-1} \sim N(\hat{\vec{x}}^{+}_{k-1},\sum\nolimits_{k-1}^{+}) \\ A&= \begin{pmatrix} \frac{\partial f_1}{\partial x^{(1)}_{k-1}} & \frac{\partial f_1}{\partial x^{(2)}_{k-1}} & \cdots & \frac{\partial f_1}{\partial x^{(n)}_{k-1}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_n}{\partial x^{(1)}_{k-1}} & \frac{\partial f_n}{\partial x^{(2)}_{k-1}} & \cdots & \frac{\partial f_n}{\partial x^{(n)}_{k-1}} \\ \end{pmatrix} \\ \vec{x}^{-}_{k} &= f(\hat{\vec{x}}^{+}_{k-1}) \\ \sum\nolimits_{k-1}^{-} &= A \sum\nolimits_{k-1}^{+} A^{T} + Q \\ C&= \begin{pmatrix} \frac{\partial h_1}{\partial x^{(1)}_{k}} & \frac{\partial h_1}{\partial x^{(2)}_{k}} & \cdots & \frac{\partial h_1}{\partial x^{(n)}_{k}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial h_n}{\partial x^{(1)}_{k}} & \frac{\partial h_n}{\partial x^{(2)}_{k}} & \cdots & \frac{\partial h_n}{\partial x^{(n)}_{k}} \\ \end{pmatrix} \\ K &= \sum\nolimits_{k}^{-} C^{T}(C \sum\nolimits_{k}^{-} C^T +R) \\ \vec{x}^{+}_k &= \vec{x}^{-}_k + K(\vec{y} -h(\vec{x}^{-}_k)) \\ \sum\nolimits_{k}^{+} &= (I - KC)\sum\nolimits_{k}^{-} \end{align*}

生成高斯噪声信号：

真实数据:xi=sin⁡(3xi−1)观测数据:yi=xi2+R\begin{align*} 真实数据:\quad x_i&=\sin(3x_{i-1}) \\ 观测数据:\quad y_i&=x_i^2+R \end{align*} 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
%生成100个信号
t = 0.01:0.01:1;
n = length(t);
x = zeros(1, n);
y = zeros(1, n);

%初值
x(1) = 0.1;
y(1) = 0.1^2;

%生成真实数据与观测数据
for i = 2:n

    x(i) = sin(3 * x(i - 1));
    y(i) = x(i)^2 + normrnd(0, 1);

end

%输出生成的信号
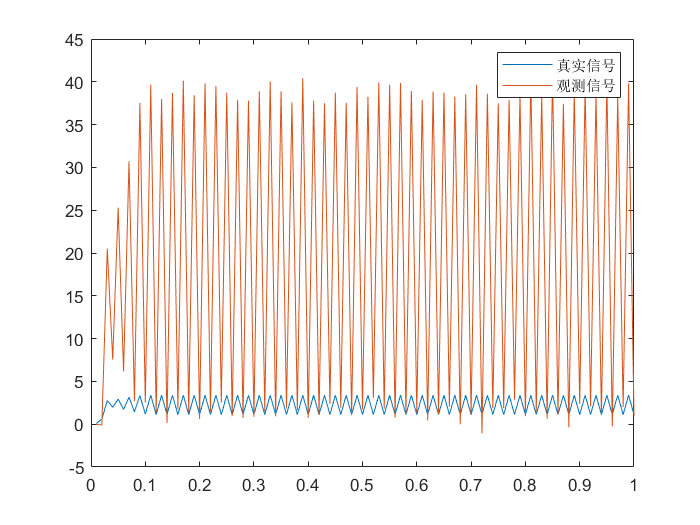
plot(t, x, 'r', t, y, 'b');
legend('真实信号', '观测信号');

高斯噪声_拓展卡尔曼滤波

注：只对一维的情况

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
function Xplus = Extend_Kalman(y, F, Q, H, R, Xplus_0, Pplus_0)

    n = length(y);
    Xplus = zeros(1, n);

    f=sym(F);
    df=diff(f);
    dF=matlabFunction(df);
    h=sym(H);
    dh=diff(h);
    dH=matlabFunction(dh);

    Pplus = Pplus_0;
    Xplus(1) = Xplus_0;

    for i = 2:n

        %预测步
        A = dF(Xplus(i - 1));
        Xminus = F(Xplus(i - 1));
        Pminus = A * Pplus * A' +Q;

        %更新步
        C = dH(Xminus);
        K = Pminus * C * inv(C * Pminus * C' +R);
        Xplus(i) = Xminus + K * (y(i) - H(Xminus));
        Pplus = (eye(1) - K * C) * Pminus;

    end

end

1
2
3
4
5
6
7
8
9
10
11
12
>> F = @(x)sin(x);
>> H = @(x)x^2;
>> Q = 1;
>> R = 1;
>> Xplus_0 = 0.01;
>> Pplus_0 = 0.01^2;

>> Xplus = Extend_Kalman(y, F, Q, H, R, Xplus_0, Pplus_0)

>> plot(t, x, 'r', t, y, 'g', t, Xplus, 'b');
>> legend('真实信号', '观测信号', '预测信号');

拓展卡尔曼滤波

原因：多峰问题。观测方程yi=xi2+Ry_i=x_i^2+R有两个解

粒子滤波器

条件：

Xk=f(xk−1)+QkYk=h(xk)+RkX0,Q1,…,Qk,R1,…,Rk相互独立\begin{align*} X_k &= f(x_{k-1}) + Q_k \\ Y_k &= h(x_k) + R_k \\ X_0,Q_1, \dots ,& Q_k,R_1, \dots , R_k 相互独立 \end{align*}

算法：

(1)初值 X0∼N(u,σ2)(2)生成n个X0样本 x0(1),…,x0(n)(3)生成X0样本对应权重 ω0(i)(ω0(i)=1n or f(x0(i))∑i=1nf(x0(i)))⋯⋯预测步开始(4)生成Xk−的样本 xk−(i)=f(x0(i))+Q预测步的分布函数 fk−(x)=∑i=1nωk−1(i)δ(x−xk(i))预测步结束观测到数据yk(5)更新步的分布函数 fk+(x)=ηfR(yk−h(x))fk−(x)=∑i=1nη fR(yk−h(x)) ωk−1(i)δ(x−xk(i))改变粒子权重 ωk(i)=fR(yk−h(x−(i)))ωk−1(i)fR=12πσe−x22σ2(6)归一化 η=(∑i=1nωk(i))−1(7)估计期望位置 x^k+=E(x)=∫−∞+∞∑i=1nωk(i)δ(x−xi)dx=∑i=1nωk(i)xi(8)方差 D(X)=E(X2)−[E(X)]2=∫−∞+∞x2f(x)dx−(∫−∞+∞x2f(x)dx)2=∑i=1n[ωk(i)xi2−(x^k+)2]更新步结束……\begin{align*} (1)&初值\ X_0 \sim N(u,\sigma ^2) \\ (2)&生成n个X_0样本\ x_0^{(1)} , \dots , x_0^{(n)} \\ (3)&生成X_0样本对应权重\ \omega_0^{(i)} \quad \bigg(\omega_0^{(i)} = \frac{1}{n} \ or \ \frac{f(x_0^{(i)})}{\sum_{i=1}^{n} f(x_0^{(i)})}\bigg) \\ &\cdots \cdots \\ &预测步开始 \\ (4)&生成X_k^{-}的样本\ x_k^{-(i)} = f(x_0^{(i)}) + Q \\ &预测步的分布函数\ f_k^{-}(x) = \sum_{i=1}^{n} \omega_{k-1}^{(i)} \delta(x - x_k^{(i)}) \\ &预测步结束 \\ &观测到数据y_k \\ (5)&更新步的分布函数\ f_k^{+}(x) = \eta f_R(y_k - h(x))f_k^{-}(x) = \sum _{i = 1}^{n} \eta \ f_R(y_k - h(x))\ \omega_{k-1}^{(i)} \delta(x - x_k^{(i)}) \\ &改变粒子权重\ \omega_k^{(i)} = f_R(y_k - h(x^{-(i)}))\omega _{k-1}^{(i)} \qquad f_R = \frac{1}{\sqrt{2\pi \sigma}} e^{-\frac{x^2}{2\sigma ^2}} \\ (6)&归一化\ \eta = (\sum_{i = 1}^{n} \omega _k^{(i)})^{-1} \\ (7)&估计期望位置\ \hat{x}_k^{+} = E(x) = \int_{-\infty}^{+\infty} \sum _{i=1}^{n} \omega_k^{(i)} \delta(x - x_i) dx = \sum_{i=1}^{n} \omega_k^{(i)}x_i \\ (8)&方差\ D(X) = E(X^2) - [E(X)]^2 = \int_{-\infty}^{+\infty} x^2f(x)dx - \bigg(\int_{-\infty}^{+\infty} x^2f(x)dx\bigg)^2 = \sum _{i=1}^{n} [\omega_k^{(i)}x_i^2- (\hat{x}_k^{+})^2] \\ &更新步结束 \\ &\dots \dots \end{align*}

生成高斯噪声信号：

真实数据:xi=sin⁡(xi−1)+5xi−1xi−12+1观测数据:yi=xi3+R\begin{align*} 真实数据:\quad x_i&=\sin(x_{i-1})+\frac{5x_{i-1}}{x_{i-1}^2+1} \\ 观测数据:\quad y_i&=x_i^3+R \end{align*} 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
%生成100个信号
t = 0.01:0.01:1;
x = zeros(1, 100);
y = zeros(1, 100);

%初值
x(1) = 0.1;
y(1) = 0.01^3;

%生成真实数据与观测数据
for i = 2:100

    x(i) = sin(x(i - 1)) + 5 * x(i - 1) / (x(i - 1)^2 + 1);
    y(i) = x(i)^3 + normrnd(0, 1);

end

%输出生成的信号
plot(t, x, t, y);
legend('真实信号','观测信号');

高斯噪声_粒子滤波

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
function Xplus = Particle_Filter(y, F, Q, H, R, n, Nth, Xplus_0)

    L = length(y);

    %设粒子集合
    Xold = zeros(1, n); %重采样前粒子
    Xnew = zeros(1, n); %重采样后粒子
    Xplus = zeros(1, L); %滤波值，即后验概率期望
    w = zeros(1, n); %粒子权重集合

    %设置初值x0(i)
    for i = 1:n

        Xold(i) = Xplus_0;
        w(i) = 1 / n;

    end

    for i = 2:L

        %预测步，由x0推出x1
        for j = 1:n

            Xold(j) = F(Xold(j)) + normrnd(0, Q);

        end

        %更新步,更新粒子权重
        for j = 1:n

            %w(j) = (2 * pi * R)^(-0.5) * exp(- (y(i) - h(xold(j)))^2 / (2 * R));
            %归一化可以消去前面的系数
            w(j) = exp(- (y(i) - H(Xold(j)))^2 / (2 * R));

        end

        %归一化
        w = w / sum(w);

        %重采样
        Neff = 1 / sum(w .* w);

        if Neff < Nth * n

            c = zeros(1, n);
            c(1) = w(1);

            for j = 2:n

                %设置区间
                c(j) = c(j - 1) + w(j);

            end

            %转盘子，生成随机数，落在哪个区间
            for j = 1:n

                a = unifrnd(0, 1); %均匀分布

                for k = 1:n

                    if a < c(k)

                        Xnew(j) = Xold(k);
                        break; %找到区间之后，跳出

                    end

                end

            end

            %把新的粒子赋给Xold
            Xold = Xnew;

            %权重都设为1/n
            for j = 1:n

                w(j) = 1 / n;

            end

        end

        %估计期望位置
        for j = 1:n
            Xplus(i) = Xplus(i) + Xold(j) * w(j);
        end

    end

end

1
2
3
4
5
6
7
8
9
10
11
12
13
>> F = @(x)sin(x) + 5 * x / (x^2 + 1)
>> H = @(x)x^3
>> Q = 1;
>> R = 1;
>> n = 100;
>> Nth = 0.5;
>> Xplus_0 = 0.01;

>> Xplus = Particle_Filter(y, F, Q, H, R, n, Nth, Xplus_0);

>> plot(t, x, 'r', t, y, 'g', t, Xplus, 'b');
>> legend('真实信号', '观测信号', '预测信号');

粒子滤波器

1
2
3
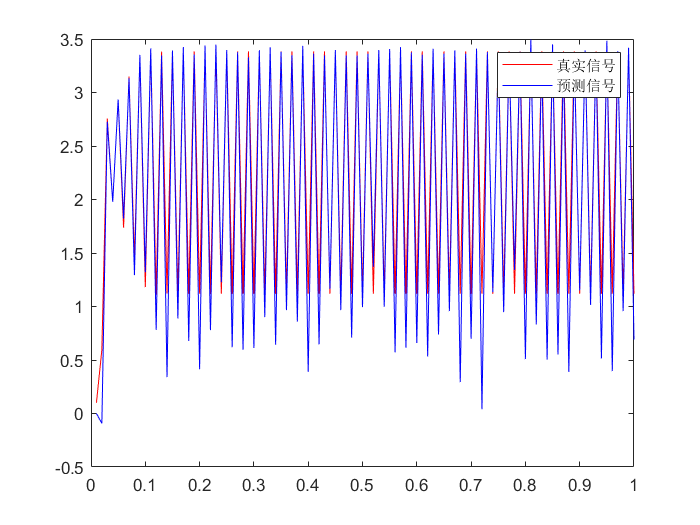
>> plot(t, x, 'r', t, Xplus, 'b');
>> legend('真实信号', '预测信号');

放大康康

感想

毕业了，其实到了最后因为一些特殊的原因(现在回想起来两个人其实也不该)我的大创就终止了，但是没想到会在最后结题答辩的时候翻车，说心里话有一些对不起我的大创老师。虽然大创可能在教授的研究生涯中根本算不上一个科研项目，但是对于我们本科生而言真的是提前开眼。感谢我们的大创老师的栽培以及研究生学长学姐的相助，若没有本科的大创的科研训练，恐怕我研究生的项目也无法如此快速的入手。