前言

虽然这门课叫做心理统计，但是统计的内容几乎不涵盖任何数学公式以及相应的公式推导证明，即使刘红云老师是数学科班出身…据她说，她也是在心理学部摸爬滚打摸索出一条不讲任何数学公式的统计课，适合心理学部宝宝的体质。

多元回归分析

导入包与数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 导入包
library(haven)
library(car)
library(olsrr)
library(psych)
library(ggplot2)
library(broom)
library(ppcor)
library(lm.beta)

# 导入数据
setwd("/Users/nanxu/研究生课程作业/心理统计/多元回归个人作业数据文件/")
data <- read_sav("./3_1.sav")

# 查看数据
names(data)
dim(data)

标准多元回归

1
2
3
4
5
# 进行多元回归分析
model <- lm(timedrs ~ phyheal + menheal + stress, data = data)

# 查看模型摘要
summary(model)

模型拟合情况

1
2
3
Residual standard error: 10.13 on 356 degrees of freedom
Multiple R-squared:  0.211,	Adjusted R-squared:  0.2044 
F-statistic: 31.74 on 3 and 356 DF,  p-value: < 2.2e-16

三个自变量总共可以解释因变量变异的21.1%

标准化回归系数

1
2
# 标准化回归系数
lm.beta(model)
1
2
3
Standardized Coefficients::
(Intercept)     phyheal     menheal      stress 
         NA 0.359931424 0.008328805 0.193065466

方差分析

1
2
# 方差分析
anova(model)
1
2
3
4
5
6
Response: timedrs
           Df Sum Sq Mean Sq F value    Pr(>F)    
phyheal     1   8154  8154.1 79.4912 < 2.2e-16 ***
menheal     1    110   110.5  1.0769 0.3000946    
stress      1   1502  1501.7 14.6391 0.0001537 ***
Residuals 356  36518   102.6

多重共线性

多重共线性指标

1
2
3
4
5
6
7
8
9
10
11
# 多重共线性指标
# 计算 VIF
vif(model)
# 计算 TOL（容忍度）
1/vif(model)
# 计算条件指数
# ols_eigen_cindex(model)

# 进行标准化自变量的多元回归分析
model_std <- lm(timedrs ~ scale(phyheal) + scale(menheal) + scale(stress), data = data)
ols_eigen_cindex(model_std)
1
2
3
4
5
6
7
8
9
10
11
12
> vif(model)
 phyheal  menheal   stress 
1.361953 1.402107 1.148871 
> 1/vif(model)
  phyheal   menheal    stress 
0.7342395 0.7132121 0.8704199 
> ols_eigen_cindex(model_std)
  Eigenvalue Condition Index intercept scale(phyheal) scale(menheal) scale(stress)
1  1.7531868        1.000000         0      0.1521228     0.15623913    0.12546381
2  1.0000000        1.324080         1      0.0000000     0.00000000    0.00000000
3  0.7483957        1.530553         0      0.1797878     0.07500899    0.85837173
4  0.4984175        1.875502         0      0.6680894     0.76875189    0.01616446

容忍度TOL大于0.1，且方差膨胀因子VIF小于10，并且条件指数CI为1.875502，三个变量不存在明显的多重共线性问题

残差分析

残差统计量

1
2
3
4
5
# 残差统计量
describe(fitted(model))
describe(residuals(model))
describe(scale(fitted(model)))
describe(scale(residuals(model)))

根据3SD原则，标准化残差的绝对值大雨3对应的观测值为异常值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
> describe(fitted(model))
   vars   n mean   sd median trimmed  mad   min   max range skew kurtosis   se
X1    1 360 8.04 5.22   7.37    7.58 4.69 -0.65 26.98 27.63 0.94     1.03 0.27
> # 残差统计量
> describe(fitted(model))
   vars   n mean   sd median trimmed  mad   min   max range skew kurtosis   se
X1    1 360 8.04 5.22   7.37    7.58 4.69 -0.65 26.98 27.63 0.94     1.03 0.27
> describe(residuals(model))
   vars   n mean    sd median trimmed  mad    min   max range skew kurtosis   se
X1    1 360    0 10.09  -2.02   -1.72 4.03 -15.87 64.22 80.09 3.27    13.56 0.53
> describe(scale(fitted(model)))
   vars   n mean sd median trimmed mad   min  max range skew kurtosis   se
X1    1 360    0  1  -0.13   -0.09 0.9 -1.67 3.63   5.3 0.94     1.03 0.05
> describe(scale(residuals(model)))
   vars   n mean sd median trimmed mad   min  max range skew kurtosis   se
X1    1 360    0  1   -0.2   -0.17 0.4 -1.57 6.37  7.94 3.27    13.56 0.05

本数据集中存在异常值

Durbin-Watson 检验

1
2
# 进行 Durbin-Watson 检验
durbinWatsonTest(model)
1
2
3
4
> durbinWatsonTest(model)
 lag Autocorrelation D-W Statistic p-value
   1       0.7842281     0.3184074       0
 Alternative hypothesis: rho != 0

Durbin-Watson 检验结果为0.3184074，认为残差可能存在正相关

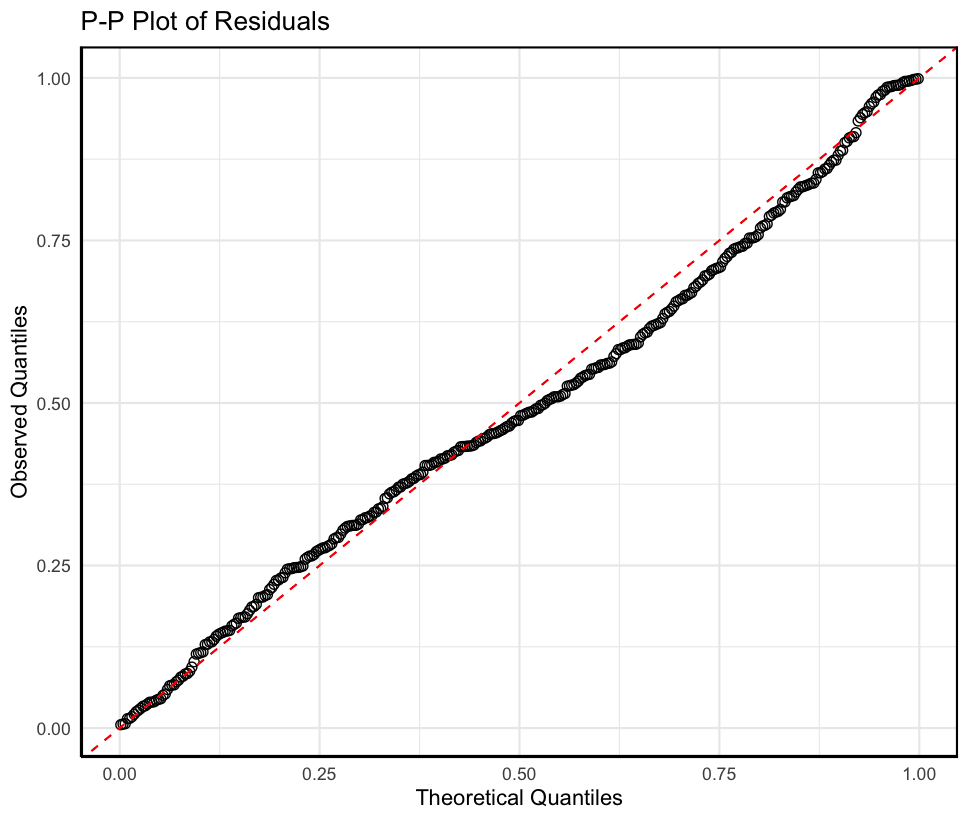
P-P 图 残差累计概率图的散点图

残差的正态性假设指的是每个因变量的预测分数下的残差都呈正态分布。若在P-P图三所有标准化残差都分布在对角线上，则可认为没有违背正态性假设。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# P-P 图  残差累计概率图的散点图
pp_data <- data.frame(
  # 计算正态分布的累计概率
  Observed = sort(pnorm(scale(residuals(model)))),
  # 生成理论上的正态分布的累计概率
  Theoretical = sort(ppoints(length(scale(residuals(model)))))
)

# 绘制 P-P 图
pp_plot <- ggplot(pp_data, aes(x = Theoretical, y = Observed)) +
  geom_point(size = 2, shape = 1) +
  geom_abline(intercept = 0, slope = 1, color = "red", linetype = "dashed") +
  labs(
    title = "P-P Plot of Residuals",
    x = "Theoretical Quantiles",
    y = "Observed Quantiles"
  ) +
  theme_minimal() +
  theme(
    panel.border = element_rect(colour = "black", fill = NA, size = 1),
    axis.line = element_line(colour = "black")
  )
print(pp_plot)

残差累计概率图的散点图

残差值的点基本上没有分布中对角线上，判定残差不服从正态分布

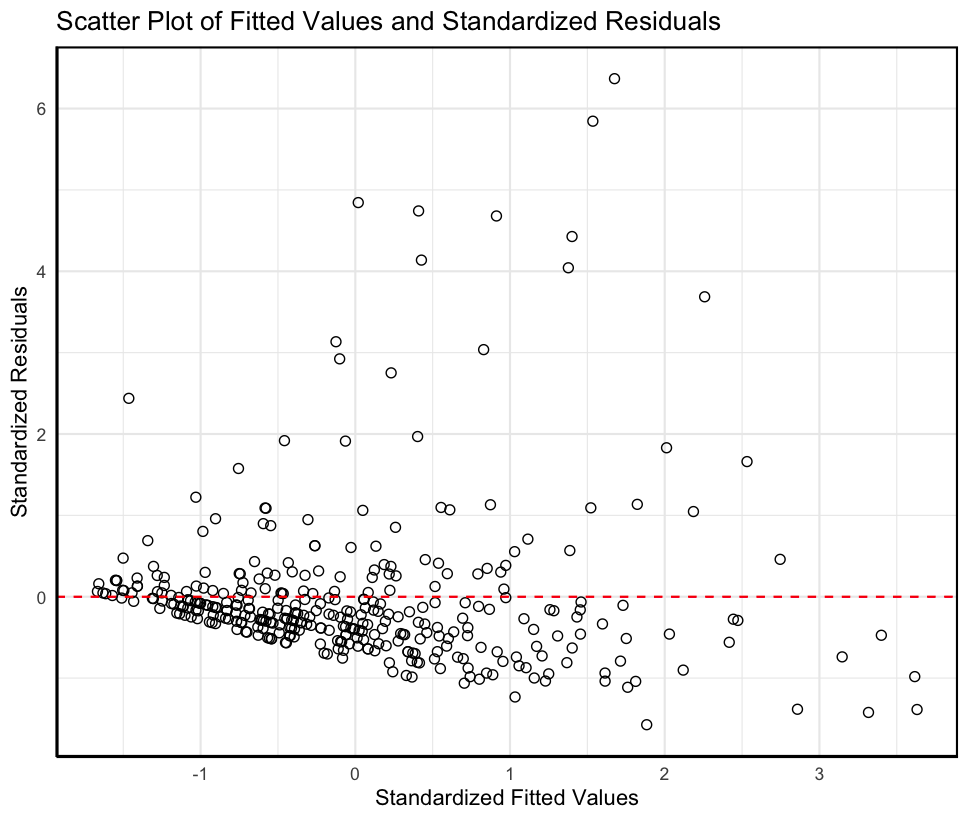
标准化因变量预测值与标准化残差的散点图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 标准化因变量预测值与标准化残差的散点图
scatter_data <- data.frame(
  Fitted = scale(fitted(model)),
  Std_Residuals = scale(residuals(model))
)

# 绘制散点图
scatter_plot <- ggplot(scatter_data, aes(x = Fitted, y = Std_Residuals)) +
  geom_point(size = 2, shape = 1) +
  geom_hline(yintercept = 0, color = "red", linetype = "dashed") +
  labs(
    title = "Scatter Plot of Fitted Values and Standardized Residuals",
    x = "Standardized Fitted Values",
    y = "Standardized Residuals"
  ) +
  theme_minimal() +
  theme(
    panel.border = element_rect(colour = "black", fill = NA, size = 1),
    axis.line = element_line(colour = "black")
  )

# 输出散点图
print(scatter_plot)

因变量预测值与标准化残差的散点图

图中各点没有随机分布在一条穿过零点的水平直线的两侧，表明残差的分布不满足正态及残差方差齐次性假设

因变量对数转换的多元回归分析

1
2
3
4
5
6
# 进行因变量对数转换的多元回归分析
model_log <- lm(logtimedrs ~ phyheal + menheal + stress, data = data)

summary(model_log)
lm.beta(model_log)
anova(model_log)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Residual standard error: 0.7752 on 356 degrees of freedom
Multiple R-squared:  0.3471,	Adjusted R-squared:  0.3416 
F-statistic: 63.08 on 3 and 356 DF,  p-value: < 2.2e-16

Standardized Coefficients::
(Intercept)     phyheal     menheal      stress 
         NA  0.49088568  0.03005799  0.18537313 

Response: logtimedrs
           Df  Sum Sq Mean Sq  F value    Pr(>F)    
phyheal     1 102.505 102.505 170.5668 < 2.2e-16 ***
menheal     1   1.429   1.429   2.3773     0.124    
stress      1   9.801   9.801  16.3087 6.594e-05 ***
Residuals 356 213.945   0.601

可见因变量对数转换后的回归方程R2有所升高，回归方程更加显著

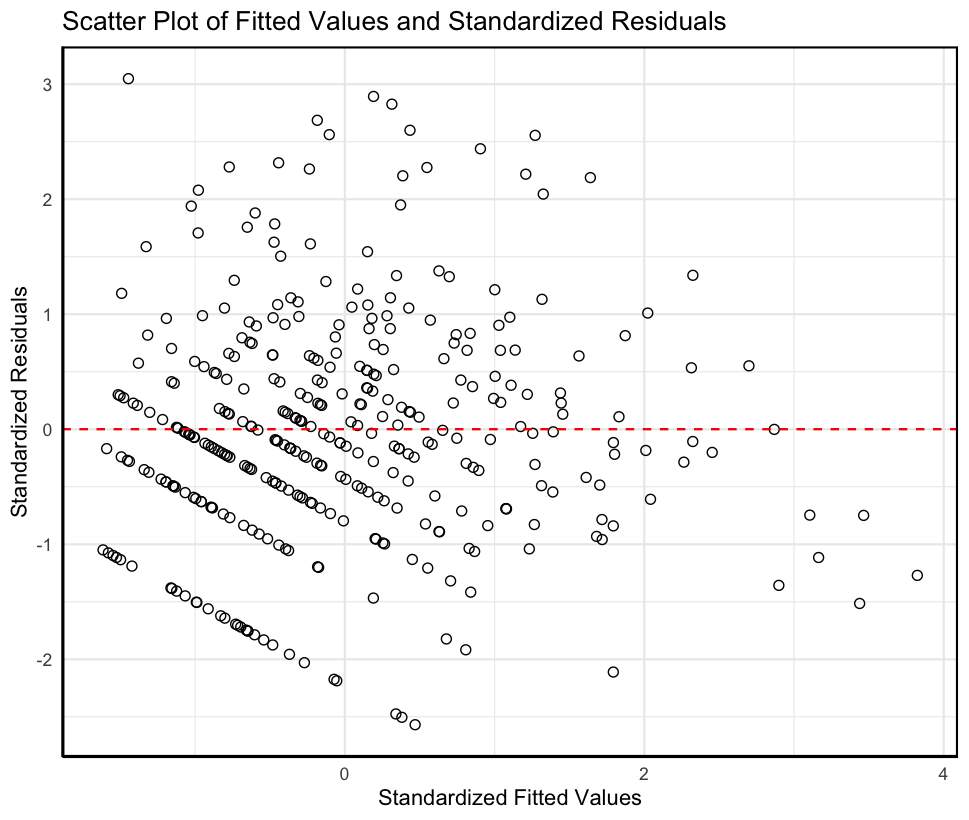
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
# 绘制 P-P 图
pp_data <- data.frame(
  # 计算正态分布的累计概率
  Observed = sort(pnorm(scale(residuals(model_log)))),
  # 生成理论上的正态分布的累计概率
  Theoretical = sort(ppoints(length(scale(residuals(model_log)))))
)
pp_plot <- ggplot(pp_data, aes(x = Theoretical, y = Observed)) +
  geom_point(size = 2, shape = 1) +
  geom_abline(intercept = 0, slope = 1, color = "red", linetype = "dashed") +
  labs(
    title = "P-P Plot of Residuals",
    x = "Theoretical Quantiles",
    y = "Observed Quantiles"
  ) +
  theme_minimal() +
  theme(
    panel.border = element_rect(colour = "black", fill = NA, size = 1),
    axis.line = element_line(colour = "black")
  )
print(pp_plot)

# 因变量预测值与标准化残差的散点图
scatter_data <- data.frame(
  Fitted = scale(fitted(model_log)),
  Std_Residuals = scale(residuals(model_log))
)

scatter_plot <- ggplot(scatter_data, aes(x = Fitted, y = Std_Residuals)) +
  geom_point(size = 2, shape = 1) +
  geom_hline(yintercept = 0, color = "red", linetype = "dashed") +
  labs(
    title = "Scatter Plot of Fitted Values and Standardized Residuals",
    x = "Standardized Fitted Values",
    y = "Standardized Residuals"
  ) +
  theme_minimal() +
  theme(
    panel.border = element_rect(colour = "black", fill = NA, size = 1),
    axis.line = element_line(colour = "black")
  )

print(scatter_plot)

因变量对数转换后的残差累计概率图的散点图

因变量对数转换后的因变量预测值与标准化残差的散点图

因变量对数转换后的回归方程基本满足正态性假设以及残差方差齐次性假设

提取回归系数估计和95%置信区间

1
2
# 提取回归系数估计和95%置信区间
tidy(model_log, conf.int = TRUE, conf.level = 0.95)
1
2
3
4
5
6
7
8
> tidy(model_log, conf.int = TRUE, conf.level = 0.95)
# A tibble: 4 × 7
  term        estimate std.error statistic  p.value  conf.low conf.high
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>     <dbl>     <dbl>
1 (Intercept)  0.402    0.105        3.83  1.50e- 4  0.195      0.608  
2 phyheal      0.204    0.0208       9.82  2.63e-20  0.163      0.245  
3 menheal      0.00681  0.0115       0.593 5.54e- 1 -0.0158     0.0294 
4 stress       0.00132  0.000327     4.04  6.59e- 5  0.000677   0.00196

相关系数

零相关系数

1
2
# 计算零相关系数
corr.test(data[c("logtimedrs", "phyheal", "menheal", "stress")])
1
2
           logtimedrs phyheal menheal stress
logtimedrs       1.00    0.56    0.34   0.34

偏相关系数

1
2
# 计算偏相关系数
pcor(data[c("logtimedrs", "phyheal", "menheal", "stress")])
1
2
           logtimedrs    phyheal    menheal     stress
logtimedrs 1.00000000 0.46174569 0.03139996 0.20929484

半偏相关系数

1
2
# 计算半偏相关系数
spcor(data[c("logtimedrs", "phyheal", "menheal", "stress")])
1
2
           logtimedrs    phyheal    menheal     stress
logtimedrs 1.00000000 0.42062902 0.02538454 0.17294627

序列回归

1
2
3
4
5
6
7
8
9
10
11
12
# 拟合回归模型，逐步添加变量
# 第一步：仅包含 phyheal
model1 <- lm(logtimedrs ~ phyheal, data = data)
summary(model1, standardized=TRUE)
lm.beta(model1)
# 计算零相关系数
corr.test(data[c("logtimedrs", "phyheal")])
# 计算偏相关系数
pcor(data[c("logtimedrs", "phyheal")])
# 计算半偏相关系数
spcor(data[c("logtimedrs", "phyheal")])

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
> summary(model1, standardized=TRUE)
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.57627    0.09877   5.834 1.21e-08 ***
phyheal      0.23250    0.01821  12.766  < 2e-16 ***
---
Residual standard error: 0.7931 on 358 degrees of freedom
Multiple R-squared:  0.3128,	Adjusted R-squared:  0.3109 
F-statistic:   163 on 1 and 358 DF,  p-value: < 2.2e-16

> lm.beta(model1)
Standardized Coefficients::
(Intercept)     phyheal 
         NA   0.5593045 

> # 计算零相关系数
> corr.test(data[c("logtimedrs", "phyheal")])
Correlation matrix 
           logtimedrs phyheal
logtimedrs       1.00    0.56

> # 计算偏相关系数
> pcor(data[c("logtimedrs", "phyheal")])
           logtimedrs   phyheal
logtimedrs  1.0000000 0.5593045

> # 计算半偏相关系数
> spcor(data[c("logtimedrs", "phyheal")])
           logtimedrs   phyheal
logtimedrs  1.0000000 0.5593045

身体健康症状phyheal的零阶相关系数、偏相关系数与半偏相关系数相等

1
2
3
4
5
6
7
8
9
10
# 第二步：添加 stress
model2 <- lm(logtimedrs ~ phyheal + stress, data = data)
lm.beta(model2)
summary(model2, standardized=TRUE)
# 计算零相关系数
corr.test(data[c("logtimedrs", "phyheal", "stress")])
# 计算偏相关系数
pcor(data[c("logtimedrs", "phyheal", "stress")])
# 计算半偏相关系数
spcor(data[c("logtimedrs", "phyheal", "stress")])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
> summary(model2, standardized=TRUE)
Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.4074062  0.1041975   3.910  0.00011 ***
phyheal     0.2095523  0.0185741  11.282  < 2e-16 ***
stress      0.0013633  0.0003181   4.286 2.35e-05 ***
---
Residual standard error: 0.7745 on 357 degrees of freedom
Multiple R-squared:  0.3464,	Adjusted R-squared:  0.3428 
F-statistic: 94.62 on 2 and 357 DF,  p-value: < 2.2e-16

> lm.beta(model2)
Standardized Coefficients::
(Intercept)     phyheal      stress 
         NA   0.5041089   0.1915007 

> # 计算零相关系数
> corr.test(data[c("logtimedrs", "phyheal", "stress")])
           logtimedrs phyheal stress
logtimedrs       1.00    0.56   0.34

> # 计算偏相关系数
> pcor(data[c("logtimedrs", "phyheal", "stress")])
           logtimedrs   phyheal    stress
logtimedrs  1.0000000 0.5126673 0.2212089

> # 计算半偏相关系数
> spcor(data[c("logtimedrs", "phyheal", "stress")])
           logtimedrs   phyheal    stress
logtimedrs  1.0000000 0.4827156 0.1833739
1
2
3
# 第三步：添加 menheal
model3 <- lm(logtimedrs ~ phyheal + stress + menheal, data = data)
summary(model3, standardized=TRUE)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
> summary(model3, standardized=TRUE)
Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.4015263  0.1047630   3.833  0.00015 ***
phyheal     0.2040556  0.0207754   9.822  < 2e-16 ***
stress      0.0013197  0.0003268   4.038 6.59e-05 ***
menheal     0.0068070  0.0114839   0.593  0.55373    
---
Residual standard error: 0.7752 on 356 degrees of freedom
Multiple R-squared:  0.3471,	Adjusted R-squared:  0.3416 
F-statistic: 63.08 on 3 and 356 DF,  p-value: < 2.2e-16

> lm.beta(model3)
Standardized Coefficients::
(Intercept)     phyheal      stress     menheal 
         NA  0.49088568  0.18537313  0.03005799 

> # 计算零相关系数
> corr.test(data[c("logtimedrs", "phyheal", "menheal", "stress")])
           logtimedrs phyheal menheal stress
logtimedrs       1.00    0.56    0.34   0.34

> # 计算偏相关系数
> pcor(data[c("logtimedrs", "phyheal", "menheal", "stress")])
           logtimedrs    phyheal    menheal     stress
logtimedrs 1.00000000 0.46174569 0.03139996 0.20929484

> # 计算半偏相关系数
> spcor(data[c("logtimedrs", "phyheal", "menheal", "stress")])
           logtimedrs    phyheal    menheal     stress
logtimedrs 1.00000000 0.42062902 0.02538454 0.17294627

可以看出，模型三加入menheal并没有带来R2显著的变化，表明新加入的变量对预测因变量没有显著的贡献。并且心理健康症状menheal的标准化系数为0.03005799，不能显著预测看病次数。偏相关系数为0.03139996且半偏相关系数为0.02538454，与零阶相关系数0.34相差较大，表明menheal不能预测看病次数。

1
2
3
4
5
6
7
8
9
10
> anova(model1, model2, model3)
Analysis of Variance Table

Model 1: logtimedrs ~ phyheal
Model 2: logtimedrs ~ phyheal + stress
Model 3: logtimedrs ~ phyheal + stress + menheal
  Res.Df    RSS Df Sum of Sq       F    Pr(>F)    
1    358 225.18                                   
2    357 214.16  1   11.0186 18.3347 2.386e-05 ***
3    356 213.94  1    0.2111  0.3513    0.5537

EFA

导入包与数据

1
2
3
4
5
6
7
8
9
10
11
12
# 导入包
library(haven)
library(psych)
library(GPArotation)

# 导入数据
setwd("/Users/nanxu/研究生课程作业/心理统计/课件数据/7第七章 探索性因素分析/")
data <- read_sav("./7_2.sav")

# 查看数据
names(data)
dim(data)

数据预处理

1
2
3
4
5
6
7
8
9
10
11
12
13
# 选择Q1-Q32
analysis_data <- data[, 1:32]

# 缺失值处理
analysis_data[analysis_data == -1] <- NA
colSums(is.na(analysis_data))

# 描述数据
# summary(analysis_data)
describe(analysis_data)

# 删除缺失值

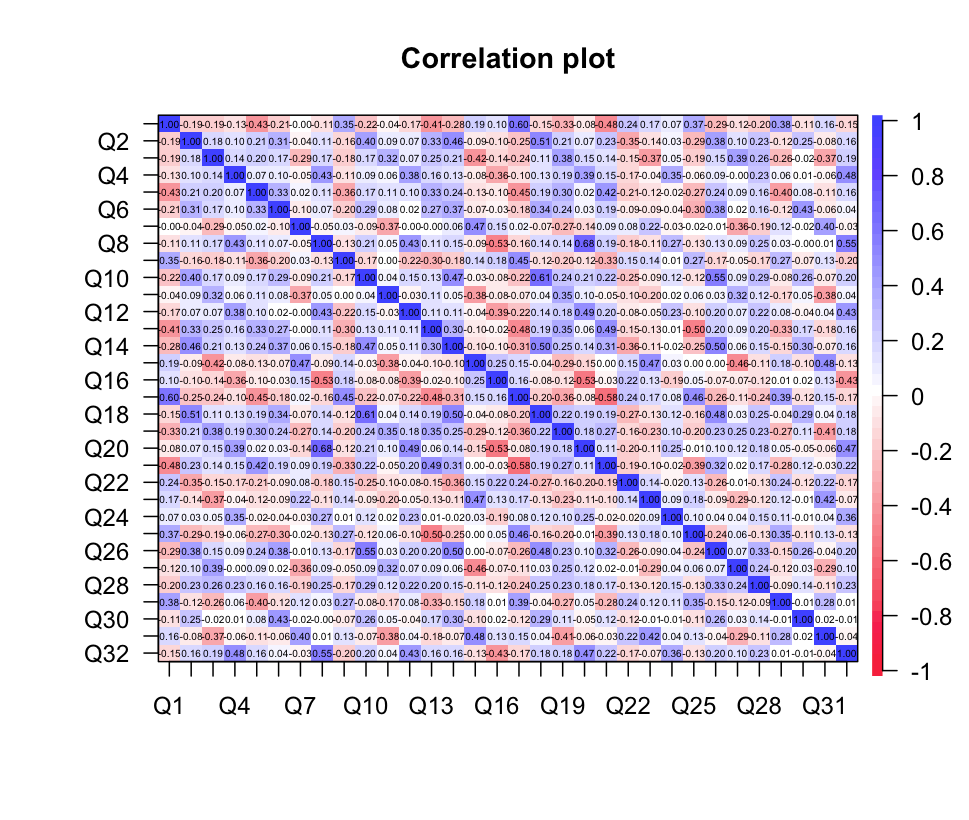
1
2
3
4
5
6
7
8
9
# 计算相关系数矩阵
cor_matrix <- cor(analysis_data, use="complete.obs")
cor.plot(cor_matrix)

# KMO检验 与 MSA
KMO(cor_matrix)

# Bartlett's 检验
cortest.bartlett(cor_matrix, n = nrow(analysis_data))

相关矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
> KMO(cor_matrix)
Kaiser-Meyer-Olkin factor adequacy
Call: KMO(r = cor_matrix)
Overall MSA =  0.86
MSA for each item = 
  Q1   Q2   Q3   Q4   Q5   Q6   Q7   Q8   Q9  Q10  Q11  Q12  Q13  Q14  Q15  Q16  Q17  Q18  Q19  Q20  Q21  Q22  Q23  Q24  Q25  Q26  Q27 
0.91 0.90 0.90 0.87 0.87 0.79 0.79 0.82 0.91 0.85 0.86 0.88 0.89 0.90 0.82 0.86 0.88 0.83 0.91 0.82 0.89 0.85 0.81 0.82 0.83 0.88 0.83 
 Q28  Q29  Q30  Q31  Q32 
0.87 0.87 0.76 0.82 0.90 

> cortest.bartlett(cor_matrix, n = nrow(analysis_data))
$chisq
[1] 4504.689

$p.value
[1] 0

$df
[1] 496

KMO的值为0.86大于0.5接近1；Bartlett球形检验结果是显著的；反映像相关矩阵MSA都大于0.5，适合做因素分析。

确定因子数目

1
2
3
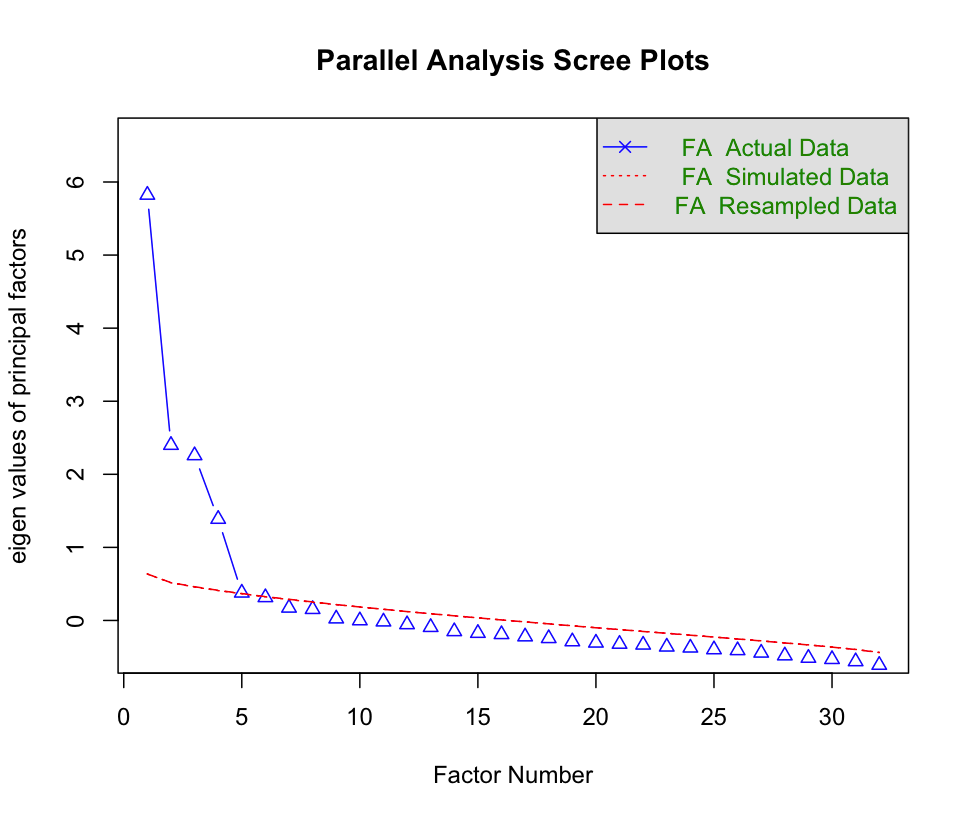
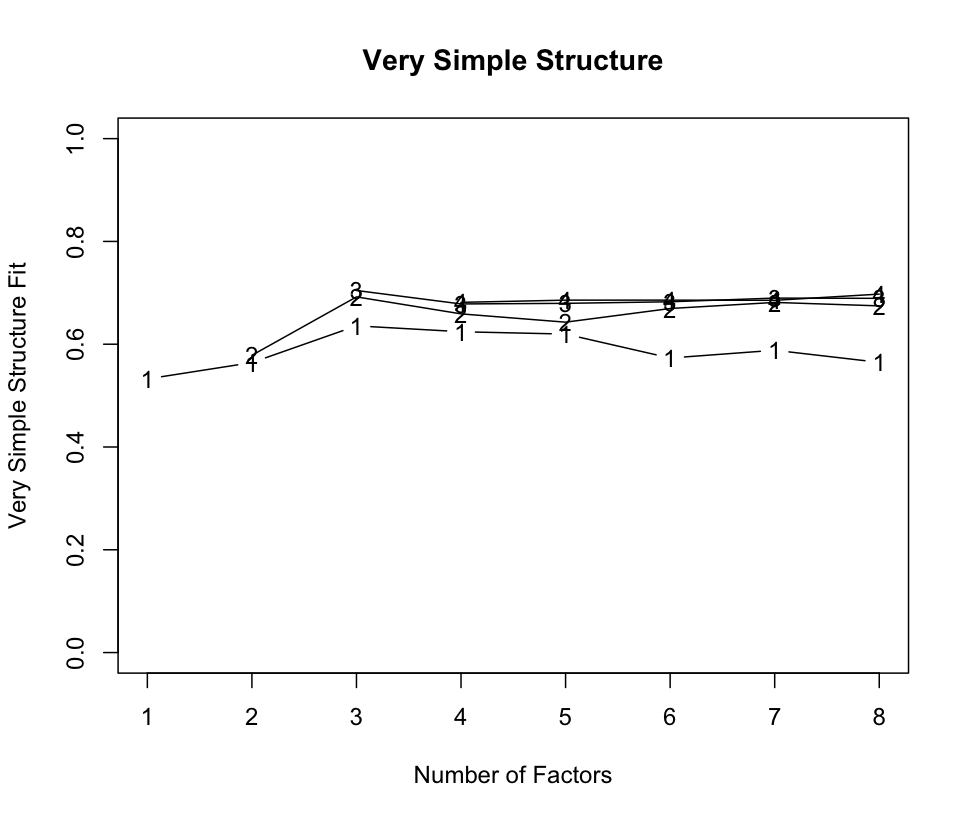
# 估计合适的因子个数
fa.parallel(analysis_data, fa="fa", n.iter=500)
vss(analysis_data, rotate = "promax", fm = "pa")

碎石图

vvs

可以看出，碎石图的拐点位于5个因素的位置

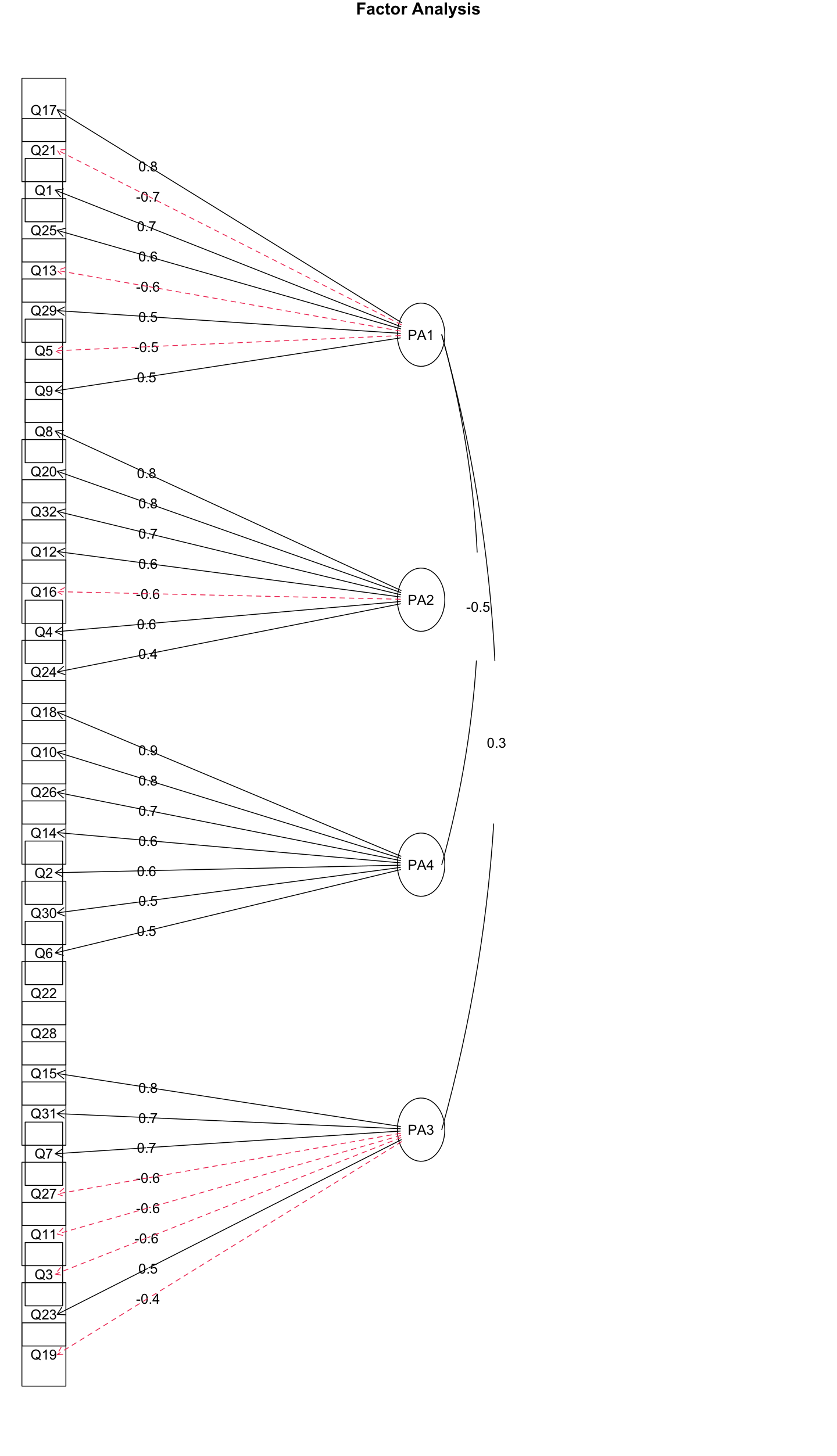
因素数固定为7的探索性因素分析

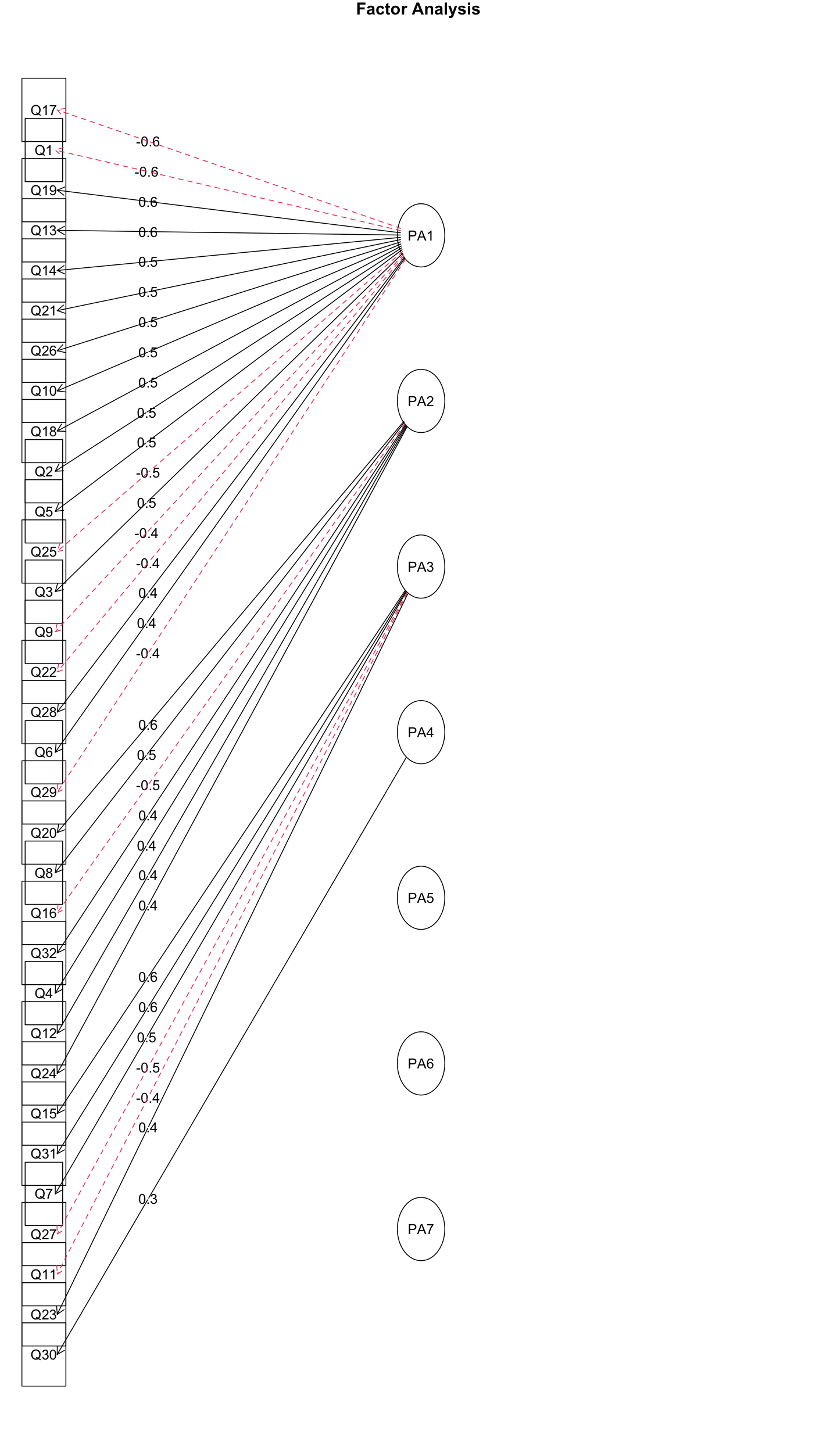
1
2
3
4
5
6
7
8
9
10
11
12
13
# 公共因素模型 主轴因素法 因子数为7
efa_7_pa <- fa(analysis_data, nfactors=7, rotate="none", fm="pa")
# 总体方差解释
efa_7_pa$Vaccounted
# 共同度
efa_7_pa$communality
# 成分矩阵
efa_7_pa$loadings
# 只显示大于0.3的载荷
print(efa_7_pa$loadings, cutoff=0.3)
# 可视化
plot(efa_7_pa)
fa.diagram(efa_7_pa)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
> efa_7_pa$Vaccounted
                            PA1        PA2        PA3        PA4        PA5        PA6        PA7
SS loadings           6.0813377 2.73434132 2.61094942 1.65202904 0.64506901 0.56737623 0.45388757
Proportion Var        0.1900418 0.08544817 0.08159217 0.05162591 0.02015841 0.01773051 0.01418399
Cumulative Var        0.1900418 0.27548997 0.35708214 0.40870804 0.42886645 0.44659696 0.46078095
Proportion Explained  0.4124342 0.18544206 0.17707366 0.11204002 0.04374835 0.03847925 0.03078249
Cumulative Proportion 0.4124342 0.59787622 0.77494988 0.88698990 0.93073825 0.96921751 1.00000000
> efa_7_pa$communality
       Q1        Q2        Q3        Q4        Q5        Q6        Q7        Q8        Q9       Q10       Q11       Q12       Q13 
0.5301886 0.4358322 0.4134696 0.4153618 0.3550281 0.3194059 0.3771826 0.6217469 0.2791207 0.5942034 0.3818267 0.4474353 0.5873971 
      Q14       Q15       Q16       Q17       Q18       Q19       Q20       Q21       Q22       Q23       Q24       Q25       Q26 
0.4835861 0.6512268 0.4792159 0.6518687 0.6188608 0.4615502 0.5965053 0.5176691 0.4549469 0.3967925 0.2961682 0.4942008 0.4989878 
      Q27       Q28       Q29       Q30       Q31       Q32 
0.4268663 0.2830110 0.4525763 0.2163821 0.5086944 0.4976820 
> print(efa_7_pa$loadings, cutoff=0.3)

Loadings:
    PA1    PA2    PA3    PA4    PA5    PA6    PA7   
Q1  -0.579                                          
Q2   0.508                                          
Q3   0.467        -0.398                            
Q4   0.332  0.413                                   
Q5   0.482                                          
Q6   0.414                                          
Q7         -0.301  0.460                            
Q8   0.422  0.527  0.359                            
Q9  -0.443                                          
Q10  0.527                0.460                     
Q11               -0.443                            
Q12  0.353  0.389  0.302                            
Q13  0.556                              0.318       
Q14  0.547                                          
Q15 -0.367 -0.304  0.603                            
Q16 -0.327 -0.514                                   
Q17 -0.642                0.368                     
Q18  0.518                0.507                     
Q19  0.558                                          
Q20  0.392  0.588                                   
Q21  0.536 -0.312        -0.311                     
Q22 -0.437                       0.378              
Q23 -0.362         0.373                            
Q24         0.354                                   
Q25 -0.471  0.350                                   
Q26  0.534                0.303                     
Q27               -0.451                            
Q28  0.419                                          
Q29 -0.360         0.317                            
Q30                       0.306                     
Q31 -0.352         0.571                            
Q32  0.437  0.444

可以看出，总体方差解释率为46.078095%

并且在第7个因素上，没有任何一个变量的因素载荷绝对值大于0.3，且在第5、6个因素上，都各只有一个变量的因素载荷绝对值大于0.3

7因素探索性因素分析

因素数固定为5的探索性因素分析

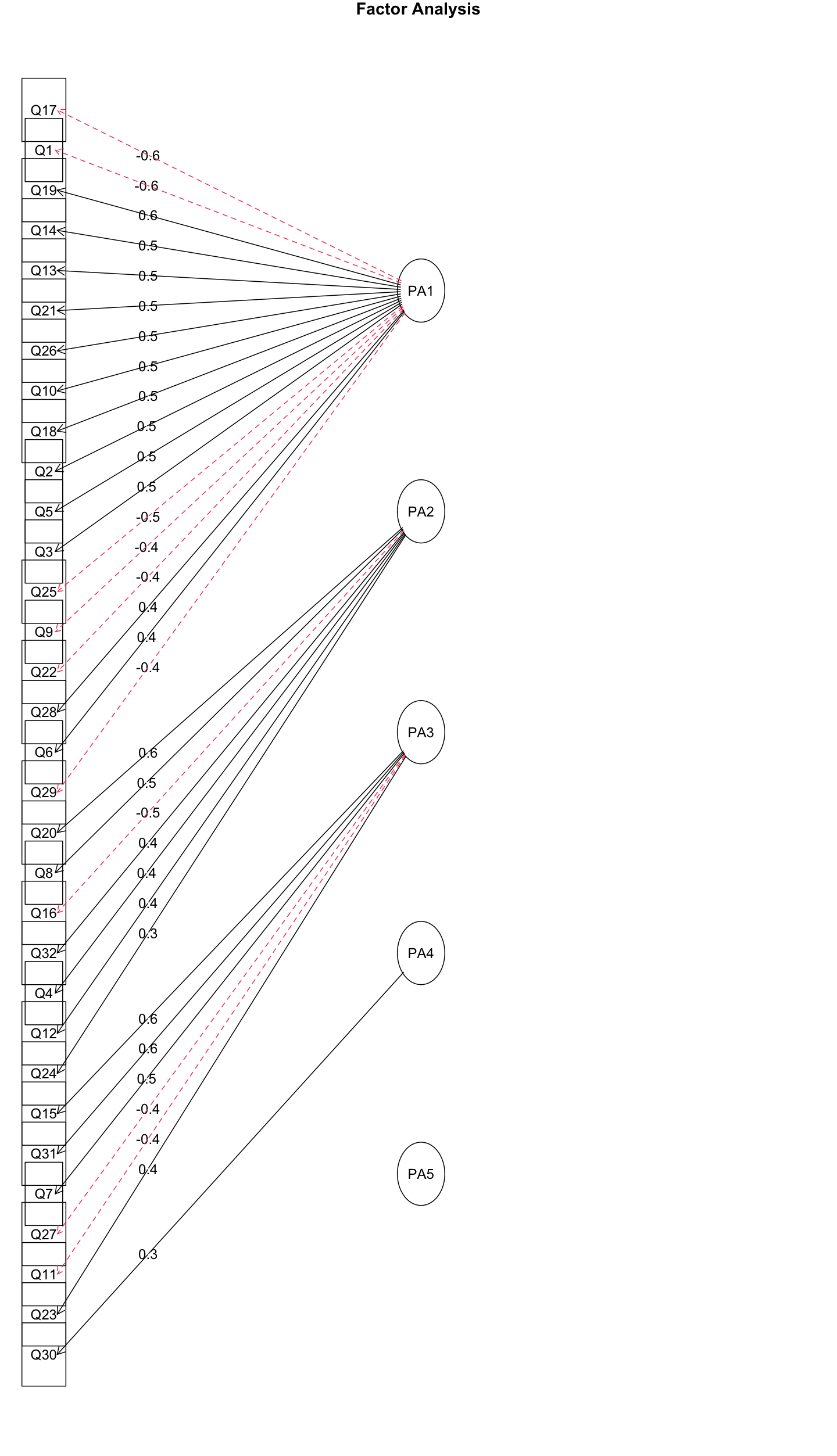
1
2
3
4
5
6
7
8
9
10
11
12
13
# 因子数为5
efa_5_pa <- fa(analysis_data, nfactors=5, rotate="none", fm="pa")
# 总体方差解释
efa_5_pa$Vaccounted
# 共同度
efa_5_pa$communality
# 成分矩阵
efa_5_pa$loadings
# 只显示大于0.3的载荷
print(efa_5_pa$loadings, cutoff=0.3)
# 可视化
plot(efa_5_pa)
fa.diagram(efa_5_pa)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
> efa_5_pa$Vaccounted
                            PA1        PA2        PA3        PA4        PA5
SS loadings           6.0447895 2.70811626 2.58239077 1.62184075 0.59269854
Proportion Var        0.1888997 0.08462863 0.08069971 0.05068252 0.01852183
Cumulative Var        0.1888997 0.27352830 0.35422802 0.40491054 0.42343237
Proportion Explained  0.4461153 0.19986340 0.19058465 0.11969450 0.04374212
Cumulative Proportion 0.4461153 0.64597873 0.83656339 0.95625788 1.00000000
> efa_5_pa$communality
       Q1        Q2        Q3        Q4        Q5        Q6        Q7        Q8        Q9       Q10       Q11       Q12       Q13 
0.4895669 0.4184995 0.4129032 0.3615361 0.3316432 0.2657098 0.3831236 0.6236585 0.2700609 0.5442838 0.3369135 0.4022832 0.4255985 
      Q14       Q15       Q16       Q17       Q18       Q19       Q20       Q21       Q22       Q23       Q24       Q25       Q26 
0.4926129 0.6275907 0.4857603 0.6250116 0.6247279 0.4436987 0.5957230 0.5273436 0.2401221 0.3335453 0.2501605 0.4073258 0.4757534 
      Q27       Q28       Q29       Q30       Q31       Q32 
0.3700609 0.2784140 0.3481493 0.1868792 0.4746635 0.4965126 
> print(efa_5_pa$loadings, cutoff=0.3)

Loadings:
    PA1    PA2    PA3    PA4    PA5   
Q1  -0.576                            
Q2   0.507                            
Q3   0.469        -0.400              
Q4   0.332  0.404                     
Q5   0.481                            
Q6   0.412                            
Q7         -0.303  0.463              
Q8   0.425  0.528  0.363              
Q9  -0.444                            
Q10  0.525                0.447       
Q11               -0.438              
Q12  0.352  0.383                     
Q13  0.542                            
Q14  0.550                            
Q15 -0.366 -0.302  0.601              
Q16 -0.330 -0.517                     
Q17 -0.640                0.371       
Q18  0.520                0.511       
Q19  0.558                            
Q20  0.395  0.588                     
Q21  0.538 -0.316        -0.321       
Q22 -0.423                            
Q23 -0.359         0.367              
Q24         0.348                     
Q25 -0.464  0.340                     
Q26  0.533                            
Q27               -0.444              
Q28  0.420                            
Q29 -0.353         0.308              
Q30                       0.301       
Q31 -0.350         0.567              
Q32  0.440  0.443

可以看出，总体方差解释率为42.343237%

并且在第5个因素上，没有任何一个变量的因素载荷绝对值大于0.3

5因素探索性因素分析

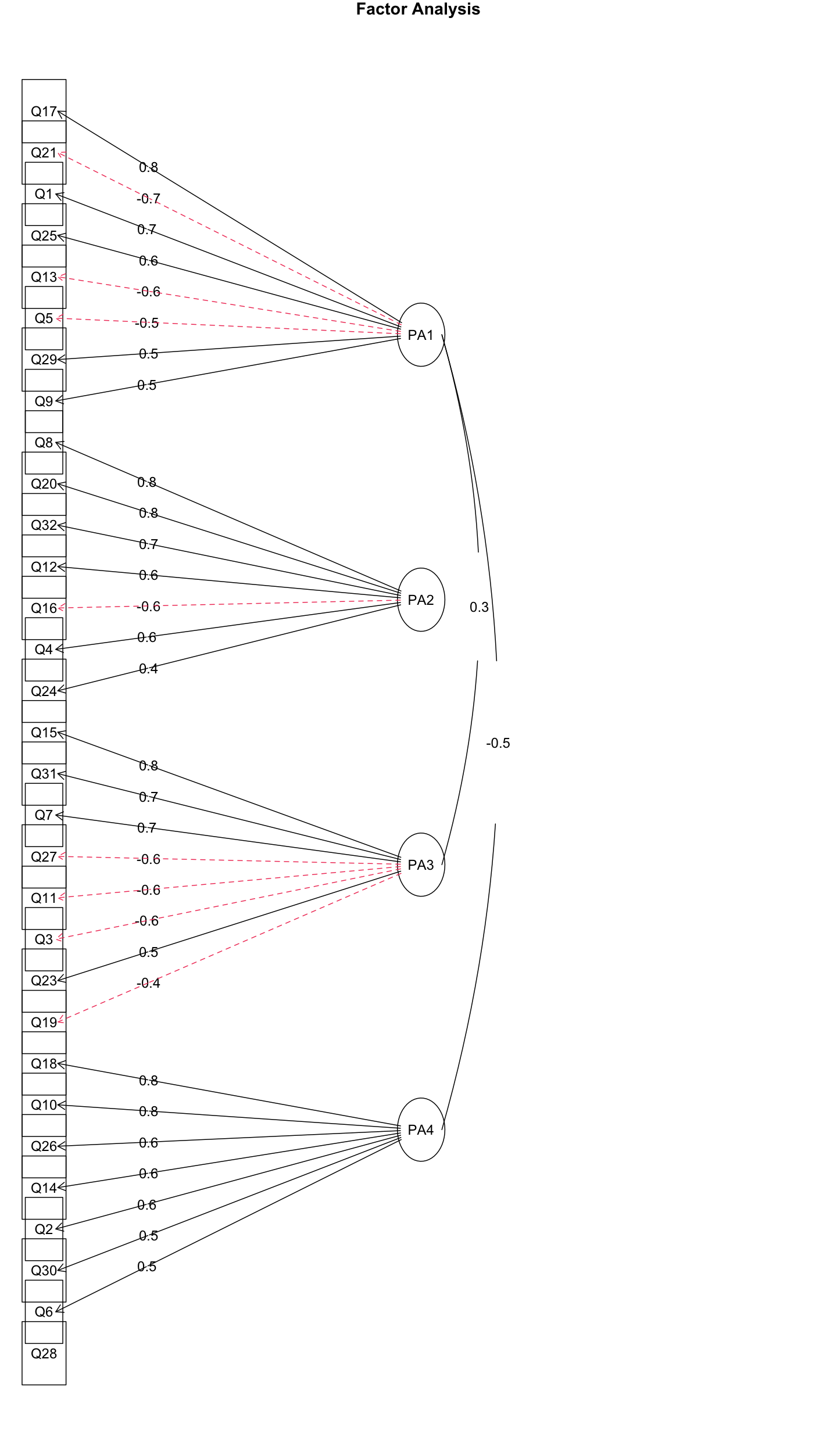
因素数固定为4的探索性因素分析

1
2
3
4
5
6
7
8
9
10
11
# 因子数为4 斜交旋转
efa_4_pa <- fa(analysis_data, nfactors=4, rotate="promax", fm="pa")
# 总体方差解释
efa_4_pa$Vaccounted
# 共同度
efa_4_pa$communality
# 成分矩阵
efa_4_pa$loadings
# 只显示大于0.3的载荷
print(efa_4_pa$loadings, cutoff=0.3)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
> efa_4_pa$Vaccounted
                            PA1        PA2       PA4        PA3
SS loadings           3.6326482 3.15732774 3.0501600 3.04880469
Proportion Var        0.1135203 0.09866649 0.0953175 0.09527515
Cumulative Var        0.1135203 0.21218675 0.3075042 0.40277940
Proportion Explained  0.2818423 0.24496410 0.2366494 0.23654424
Cumulative Proportion 0.2818423 0.52680636 0.7634558 1.00000000
> efa_4_pa$communality
       Q1        Q2        Q3        Q4        Q5        Q6        Q7        Q8        Q9       Q10       Q11       Q12       Q13 
0.4900625 0.3937478 0.4067060 0.3584038 0.3256476 0.2662986 0.3822206 0.6101605 0.2693080 0.5384912 0.3172389 0.3925288 0.4219459 
      Q14       Q15       Q16       Q17       Q18       Q19       Q20       Q21       Q22       Q23       Q24       Q25       Q26 
0.4532441 0.5764920 0.3976837 0.6248901 0.6294796 0.3836804 0.5833695 0.5209850 0.1843002 0.2696753 0.1921420 0.3905649 0.4716011 
      Q27       Q28       Q29       Q30       Q31       Q32 
0.3483654 0.2010546 0.3486561 0.1874059 0.4625831 0.4900075 
> print(efa_4_pa$loadings, cutoff=0.3)

Loadings:
    PA1    PA2    PA4    PA3   
Q1   0.700                     
Q2                 0.592       
Q3                       -0.566
Q4          0.601              
Q5  -0.546                     
Q6                 0.457       
Q7                        0.655
Q8          0.789              
Q9   0.509                     
Q10                0.765       
Q11                      -0.594
Q12         0.627              
Q13 -0.626                     
Q14                0.606       
Q15                       0.782
Q16        -0.620              
Q17  0.815                     
Q18                0.858       
Q19                      -0.427
Q20         0.762              
Q21 -0.731                     
Q22                            
Q23                       0.478
Q24         0.432              
Q25  0.639                     
Q26                0.653       
Q27                      -0.611
Q28                            
Q29  0.548                     
Q30                0.482       
Q31                       0.674
Q32         0.681

可以看出，总体方差解释率为40.277940% 有两个变量Q22与Q28在所有因素上的载荷绝对值都小于0.3。并且Q22的共同度为0.1843002，Q28的共同度为0.2010546。

4因素探索性因素分析

为了避免误删的情况，一次删除一个变量，先删除共同度更低的Q22

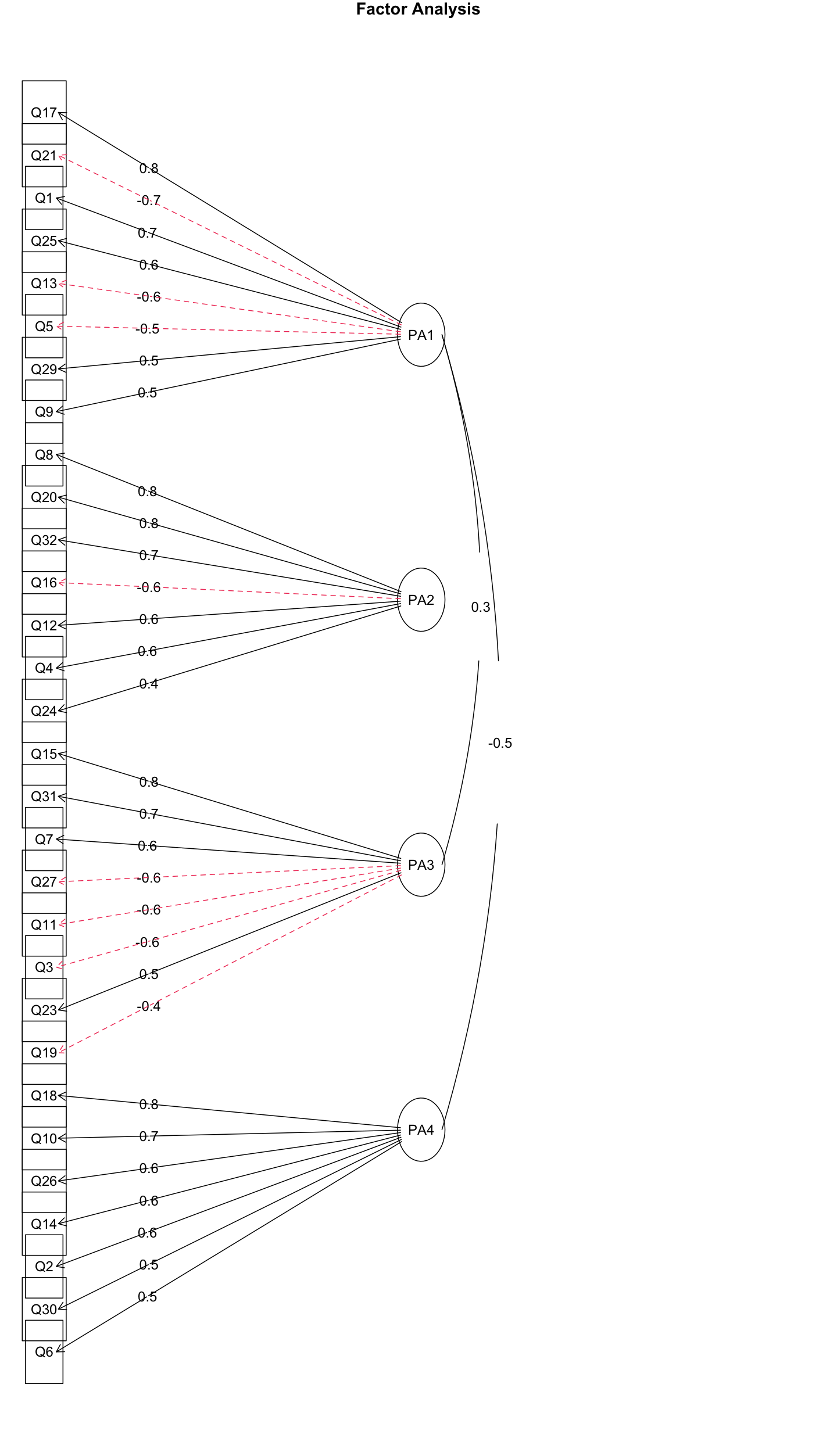
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 删去Q22
analysis_data1 <- subset(analysis_data, select = -Q22)
names(analysis_data1)

# 因子数为4 斜交旋转
efa_4_pa1 <- fa(analysis_data1, nfactors=4, rotate="promax", fm="pa")
# 总体方差解释
efa_4_pa1$Vaccounted
# 共同度
efa_4_pa1$communality
# 成分矩阵
efa_4_pa1$loadings
# 只显示大于0.3的载荷
print(efa_4_pa1$loadings, cutoff=0.3)
# 可视化
plot(efa_4_pa1)
fa.diagram(efa_4_pa1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
> efa_4_pa1$Vaccounted
                            PA1       PA2        PA3        PA4
SS loadings           3.5893385 3.1448807 3.04123134 2.92815052
Proportion Var        0.1157851 0.1014478 0.09810424 0.09445647
Cumulative Var        0.1157851 0.2172329 0.31533711 0.40979358
Proportion Explained  0.2825450 0.2475582 0.23939915 0.23049768
Cumulative Proportion 0.2825450 0.5301032 0.76950232 1.00000000
> efa_4_pa1$communality
       Q1        Q2        Q3        Q4        Q5        Q6        Q7        Q8        Q9       Q10       Q11       Q12       Q13 
0.4863391 0.3795585 0.4091628 0.3578021 0.3240189 0.2766300 0.3825274 0.6092897 0.2706913 0.5401742 0.3174019 0.3949205 0.4275838 
      Q14       Q15       Q16       Q17       Q18       Q19       Q20       Q21       Q23       Q24       Q25       Q26       Q27 
0.4403981 0.5756366 0.3959852 0.6258198 0.6288677 0.3899786 0.5801802 0.5219272 0.2694124 0.1931119 0.3943182 0.4680189 0.3528202 
      Q28       Q29       Q30       Q31       Q32 
0.2060787 0.3450362 0.1908110 0.4578422 0.4912575 
> print(efa_4_pa1$loadings, cutoff=0.3)

Loadings:
    PA1    PA2    PA3    PA4   
Q1   0.693                     
Q2                        0.570
Q3                -0.566       
Q4          0.598              
Q5  -0.541                     
Q6                        0.461
Q7                 0.651       
Q8          0.785              
Q9   0.505                     
Q10                       0.752
Q11               -0.591       
Q12         0.625              
Q13 -0.622                     
Q14                       0.586
Q15                0.776       
Q16        -0.616              
Q17  0.806                     
Q18                       0.841
Q19               -0.430       
Q20         0.758              
Q21 -0.724                     
Q23                0.476       
Q24         0.429              
Q25  0.634                     
Q26                       0.639
Q27               -0.610       
Q28                            
Q29  0.539                     
Q30                       0.476
Q31                0.667       
Q32         0.680

可以看出，总体方差解释率为40.979358% 变量Q28在所有因素上的载荷绝对值小于0.3，Q28的共同度为0.2060787。

4因素探索性因素分析

继续删除Q28变量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 删去Q28
analysis_data2 <- subset(analysis_data1, select = -Q28)
names(analysis_data2)

# 因子数为4 斜交旋转
efa_4_pa2 <- fa(analysis_data2, nfactors=4, rotate="promax", fm="pa")
# 总体方差解释
efa_4_pa2$Vaccounted
# 共同度
efa_4_pa2$communality
# 成分矩阵
efa_4_pa2$loadings
# 只显示大于0.3的载荷
print(efa_4_pa2$loadings, cutoff=0.3)
# 可视化
plot(efa_4_pa2)
fa.diagram(efa_4_pa2)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
> efa_4_pa2$Vaccounted
                            PA1       PA2        PA3        PA4
SS loadings           3.5828806 3.0766135 2.99839031 2.84177976
Proportion Var        0.1194294 0.1025538 0.09994634 0.09472599
Cumulative Var        0.1194294 0.2219831 0.32192948 0.41665547
Proportion Explained  0.2866381 0.2461357 0.23987767 0.22734849
Cumulative Proportion 0.2866381 0.5327738 0.77265151 1.00000000
> efa_4_pa2$communality
       Q1        Q2        Q3        Q4        Q5        Q6        Q7        Q8        Q9       Q10       Q11       Q12       Q13 
0.4862573 0.3824251 0.4032269 0.3536933 0.3241615 0.2812596 0.3745370 0.6094749 0.2703332 0.5315761 0.3167107 0.3900420 0.4270932 
      Q14       Q15       Q16       Q17       Q18       Q19       Q20       Q21       Q23       Q24       Q25       Q26       Q27 
0.4543375 0.5865768 0.4022270 0.6254822 0.6306127 0.3890294 0.5902971 0.5227965 0.2737261 0.1899345 0.3935340 0.4567565 0.3432978 
      Q29       Q30       Q31       Q32 
0.3456581 0.1904744 0.4630060 0.4911267 
> print(efa_4_pa2$loadings, cutoff=0.3)

Loadings:
    PA1    PA2    PA3    PA4   
Q1   0.693                     
Q2                        0.566
Q3                -0.560       
Q4          0.589              
Q5  -0.540                     
Q6                        0.459
Q7                 0.640       
Q8          0.776              
Q9   0.504                     
Q10                       0.737
Q11               -0.585       
Q12         0.612              
Q13 -0.621                     
Q14                       0.591
Q15                0.776       
Q16        -0.613              
Q17  0.807                     
Q18                       0.831
Q19               -0.432       
Q20         0.757              
Q21 -0.722                     
Q23                0.477       
Q24         0.423              
Q25  0.629                     
Q26                       0.620
Q27               -0.598       
Q29  0.539                     
Q30                       0.467
Q31                0.662       
Q32         0.673

4因素探索性因素分析

1
2
# 因素相关矩阵
efa_4_pa2$score.cor
1
2
3
4
5
6
> efa_4_pa2$score.cor
           [,1]       [,2]       [,3]       [,4]
[1,]  1.0000000 -0.1472319  0.2644861 -0.4064475
[2,] -0.1472319  1.0000000 -0.1725307  0.1851080
[3,]  0.2644861 -0.1725307  1.0000000 -0.1787275
[4,] -0.4064475  0.1851080 -0.1787275  1.0000000

可以根据每个因素下的题目的意义给因素命名

CFA

导入包与数据

1
2
3
4
5
6
7
8
9
10
11
# 导入包
library(lavaan)
library(semPlot)

# 导入数据
setwd("/Users/nanxu/研究生课程作业/心理统计/课件数据/8第八章 验证性因素分析/")
data <- read.table("./8_1.dat", header = FALSE, sep = "", na.strings = "NA")

# 查看数据
names(data)
dim(data)

数据介绍

1
2
3
4
# 描述数据
summary(data)
# library(psych)
# describe(data)

后三列数据分别是被试编码、被试年龄以及性别

探索性因素分析

第一次CFA

模型识别：待估计的参数数量t=11(因素载荷)+11(误差项方差)+1(两个因素的相关)=23 < (模型协方差矩阵的元素数)q(q+1)2\frac{q(q+1)}{2} = 66

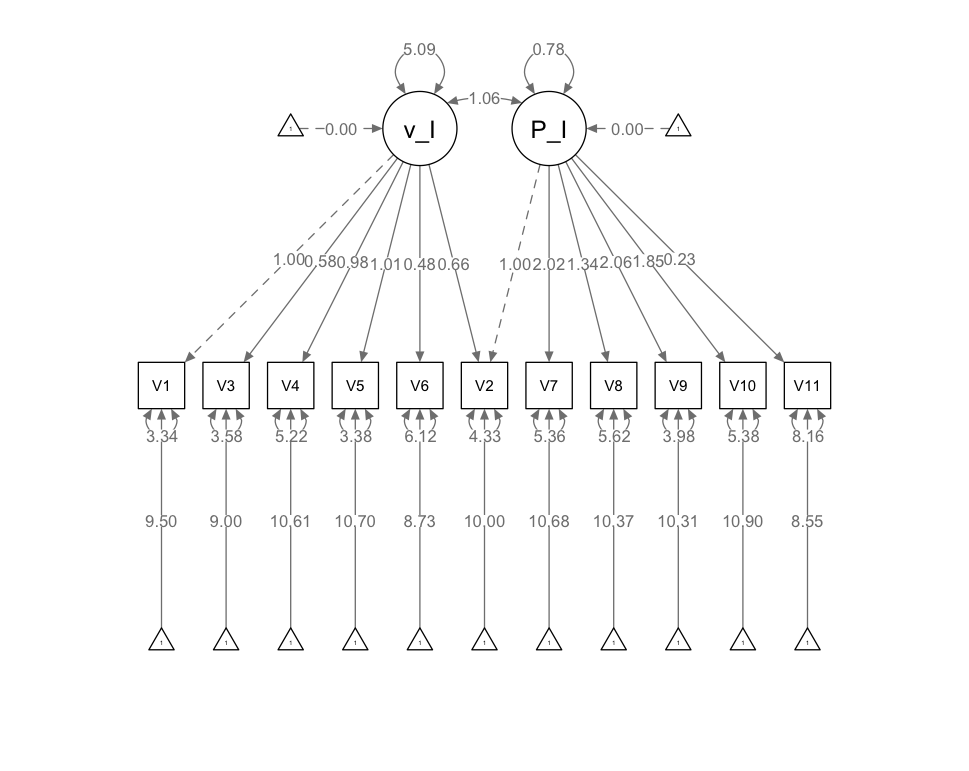
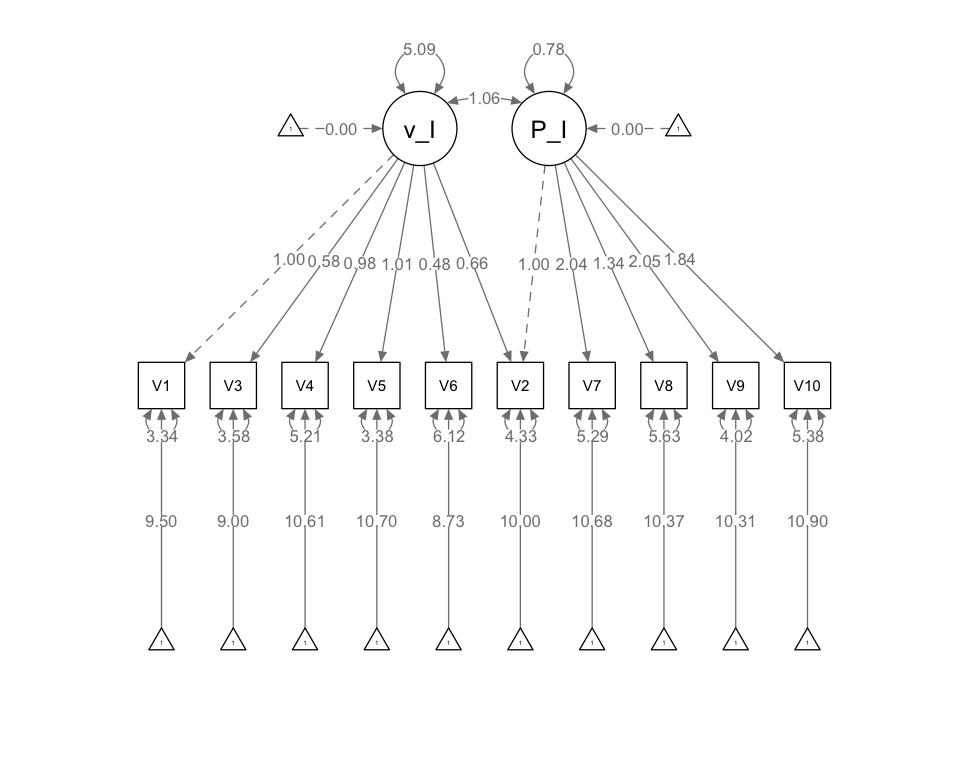
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 定义CFA模型1
model1 <- '
  # 定义潜变量 verbal_IQ
  verbal_IQ =~ V1 + V2 + V3 + V4 + V5 + V6
  
  # 定义潜变量 Performance_IQ
  Performance_IQ =~ V7 + V8 + V9 + V10 + V11
  
  # 显式请求截距
  V1 ~1
  V2 ~1
  V3 ~1
  V4 ~1
  V5 ~1
  V6 ~1
  V7 ~1
  V8 ~1
  V9 ~1
  V10 ~1
  V11 ~1
'

# 运行CFA模型
fit1 <- cfa(model1, data=data)

summary(fit1, fit.measures = TRUE, standardized=TRUE, rsquare = TRUE)

# 修正指数结果
modificationIndices(fit1, sort = TRUE, minimum.value = 4.0)

# 可视化
semPaths(fit1, whatLabels="est", layout="tree", edge.label.cex=0.8, node.label.cex=0.9)

模型拟合结果

卡方值

1
2
3
4
5
6
7
8
9
10
11
Model Test User Model:
                                                      
  Test statistic                                70.640
  Degrees of freedom                                43
  P-value (Chi-square)                           0.005

Model Test Baseline Model:

  Test statistic                               519.204
  Degrees of freedom                                55
  P-value                                        0.000

似然值与信息标准指数

1
2
3
4
5
6
7
8
Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -4491.822
  Loglikelihood unrestricted model (H1)      -4456.502
                                                      
  Akaike (AIC)                                9051.643
  Bayesian (BIC)                              9159.246
  Sample-size adjusted Bayesian (SABIC)       9051.579

相对拟合指数(比较拟合指数CFI、非标准拟合指数TLI)与绝对拟合指数(近似误差均方根RMSEA)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.940
  Tucker-Lewis Index (TLI)                       0.924


Root Mean Square Error of Approximation:

  RMSEA                                          0.061
  90 Percent confidence interval - lower         0.033
  90 Percent confidence interval - upper         0.085
  P-value H_0: RMSEA <= 0.050                    0.233
  P-value H_0: RMSEA >= 0.080                    0.103

Standardized Root Mean Square Residual:

  SRMR                                           0.054

模型的RMSEA为0.061小于0.08，CFI为0.940，TLI为0.924，均大于0.9，表明模型拟合结果良好。

模型原始估计结果

因素载荷结果的估计值、标准误差、z分数以及统计显著性检验结果，方差标准化的结果Std.all

默认采用固定因素载荷为1的方法设定潜变量的量尺，采用每个潜变量的第一个观测变量的因素载荷为1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Latent Variables:
                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  verbal_IQ =~                                                           
    V1                 1.000                               2.206    0.760
    V2                 0.926    0.108    8.609    0.000    2.042    0.691
    V3                 0.589    0.084    7.013    0.000    1.300    0.565
    V4                 1.012    0.115    8.764    0.000    2.232    0.703
    V5                 1.020    0.107    9.548    0.000    2.250    0.770
    V6                 0.477    0.099    4.805    0.000    1.053    0.390
  Performance_IQ =~                                                      
    V7                 1.000                               1.742    0.595
    V8                 0.719    0.156    4.614    0.000    1.253    0.473
    V9                 1.060    0.187    5.675    0.000    1.846    0.683
    V10                0.921    0.177    5.215    0.000    1.605    0.566
    V11                0.119    0.147    0.810    0.418    0.207    0.072

可以看出，X11在潜变量F2上的标准化因素载荷仅为0.072，且没有达到显著水平

潜变量的相关的估计值、标准误差、z分数以及统计显著性检验结果，方差标准化的结果Std.all

1
2
3
4
Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  verbal_IQ ~~                                                          
    Performance_IQ    2.263    0.515    4.397    0.000    0.589    0.589

截距的估计值、标准误差、z分数以及统计显著性检验结果，方差标准化的结果Std.all

1
2
3
4
5
6
7
8
9
10
11
12
13
Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .V1                9.497    0.220   43.264    0.000    9.497    3.270
   .V2               10.000    0.224   44.740    0.000   10.000    3.382
   .V3                9.000    0.174   51.758    0.000    9.000    3.913
   .V4               10.611    0.240   44.220    0.000   10.611    3.343
   .V5               10.703    0.221   48.416    0.000   10.703    3.660
   .V6                8.731    0.204   42.837    0.000    8.731    3.238
   .V7               10.680    0.221   48.288    0.000   10.680    3.650
   .V8               10.371    0.200   51.734    0.000   10.371    3.911
   .V9               10.314    0.204   50.496    0.000   10.314    3.817
   .V10              10.903    0.214   50.860    0.000   10.903    3.845
   .V11               8.549    0.216   39.487    0.000    8.549    2.985

误差的方差与潜变量的方差的估计值、标准误差、z分数以及统计显著性检验结果，方差标准化的结果Std.all

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .V1                3.566    0.507    7.034    0.000    3.566    0.423
   .V2                4.572    0.585    7.815    0.000    4.572    0.523
   .V3                3.602    0.420    8.571    0.000    3.602    0.681
   .V4                5.096    0.662    7.702    0.000    5.096    0.506
   .V5                3.487    0.506    6.886    0.000    3.487    0.408
   .V6                6.162    0.680    9.056    0.000    6.162    0.848
   .V7                5.526    0.757    7.296    0.000    5.526    0.646
   .V8                5.463    0.658    8.298    0.000    5.463    0.777
   .V9                3.894    0.640    6.083    0.000    3.894    0.533
   .V10               5.467    0.719    7.600    0.000    5.467    0.680
   .V11               8.159    0.874    9.335    0.000    8.159    0.995
    verbal_IQ         4.867    0.883    5.514    0.000    1.000    1.000
    Performance_IQ    3.035    0.844    3.593    0.000    1.000    1.000

R2结果

R2结果为每道题标准化因素载荷的平凡，描述了题目信度的高低

1
2
3
4
5
6
7
8
9
10
11
12
13
R-Square:
                   Estimate
    V1                0.577
    V2                0.477
    V3                0.319
    V4                0.494
    V5                0.592
    V6                0.152
    V7                0.354
    V8                0.223
    V9                0.467
    V10               0.320
    V11               0.005

修正指数结果

1
2
# 修正指数结果
modificationIndices(fit1, sort = TRUE, minimum.value = 4.0)

修正指数结果部分呈现了所有可能路径的修正指数值mi、自由估计该参数时可能的估计值epc、使用连续潜变量的方差标准化的估计值sepc.lv、使用连续潜变量及背景变量和结果变量的方差进行标准化的估计值sepc.all

1
2
3
4
5
6
7
8
9
10
11
              lhs op rhs    mi    epc sepc.lv sepc.all sepc.nox
45 Performance_IQ =~  V2 9.823  0.538   0.937    0.317    0.317
75             V3 ~~ V10 6.362 -0.945  -0.945   -0.213   -0.213
50             V1 ~~  V2 5.221 -0.985  -0.985   -0.244   -0.244
94             V6 ~~ V11 4.927  1.207   1.207    0.170    0.170
64             V2 ~~  V7 4.685  0.969   0.969    0.193    0.193
98             V7 ~~ V11 4.575 -1.225  -1.225   -0.182   -0.182
44 Performance_IQ =~  V1 4.477 -0.342  -0.596   -0.205   -0.205
53             V1 ~~  V5 4.403  0.912   0.912    0.259    0.259
86             V5 ~~  V8 4.146 -0.798  -0.798   -0.183   -0.183
51             V1 ~~  V3 4.133  0.697   0.697    0.194    0.194

看出V2可能测量了Performance_IQ这个因素

第一次CFA

修正后的第二次CFA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 修正模型
model2 <- '
  # 定义潜变量 verbal_IQ
  verbal_IQ =~ V1 + V2 + V3 + V4 + V5 + V6
  
  # 定义潜变量 Performance_IQ
  Performance_IQ =~ V2 + V7 + V8 + V9 + V10 + V11
  
  # 显式请求截距
  V1 ~1
  V2 ~1
  V3 ~1
  V4 ~1
  V5 ~1
  V6 ~1
  V7 ~1
  V8 ~1
  V9 ~1
  V10 ~1
  V11 ~1
'

fit2 <- cfa(model2, data=data)
summary(fit2, fit.measures = TRUE, standardized=TRUE, rsquare = TRUE)

# 可视化
semPaths(fit2, whatLabels="est", layout="tree", edge.label.cex=0.8, node.label.cex=0.9)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
Model Test User Model:
                                                      
  Test statistic                                60.642
  Degrees of freedom                                42
  P-value (Chi-square)                           0.031

Model Test Baseline Model:

  Test statistic                               519.204
  Degrees of freedom                                55
  P-value                                        0.000

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.960
  Tucker-Lewis Index (TLI)                       0.947

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -4486.823
  Loglikelihood unrestricted model (H1)      -4456.502
                                                      
  Akaike (AIC)                                9043.645
  Bayesian (BIC)                              9154.413
  Sample-size adjusted Bayesian (SABIC)       9043.579

Root Mean Square Error of Approximation:

  RMSEA                                          0.050
  90 Percent confidence interval - lower         0.016
  90 Percent confidence interval - upper         0.077
  P-value H_0: RMSEA <= 0.050                    0.465
  P-value H_0: RMSEA >= 0.080                    0.031

Standardized Root Mean Square Residual:

  SRMR                                           0.050
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
Latent Variables:
                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  verbal_IQ =~                                                           
    V1                 1.000                               2.256    0.777
    V2                 0.661    0.118    5.606    0.000    1.491    0.504
    V3                 0.579    0.082    7.101    0.000    1.307    0.568
    V4                 0.977    0.112    8.751    0.000    2.205    0.695
    V5                 1.008    0.103    9.739    0.000    2.273    0.777
    V6                 0.476    0.097    4.918    0.000    1.075    0.399
  Performance_IQ =~                                                      
    V2                 1.000                               0.884    0.299
    V7                 2.024    0.657    3.080    0.002    1.790    0.612
    V8                 1.345    0.470    2.862    0.004    1.189    0.448
    V9                 2.062    0.662    3.112    0.002    1.823    0.675
    V10                1.847    0.606    3.048    0.002    1.633    0.576
    V11                0.227    0.294    0.772    0.440    0.200    0.070

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  verbal_IQ ~~                                                          
    Performance_IQ    1.064    0.380    2.795    0.005    0.533    0.533

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .V1                9.497    0.220   43.264    0.000    9.497    3.270
   .V2               10.000    0.224   44.740    0.000   10.000    3.382
   .V3                9.000    0.174   51.758    0.000    9.000    3.913
   .V4               10.611    0.240   44.220    0.000   10.611    3.343
   .V5               10.703    0.221   48.416    0.000   10.703    3.660
   .V6                8.731    0.204   42.837    0.000    8.731    3.238
   .V7               10.680    0.221   48.288    0.000   10.680    3.650
   .V8               10.371    0.200   51.734    0.000   10.371    3.911
   .V9               10.314    0.204   50.496    0.000   10.314    3.817
   .V10              10.903    0.214   50.860    0.000   10.903    3.845
   .V11               8.549    0.216   39.487    0.000    8.549    2.985

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .V1                3.343    0.502    6.665    0.000    3.343    0.396
   .V2                4.331    0.554    7.819    0.000    4.331    0.495
   .V3                3.584    0.420    8.533    0.000    3.584    0.677
   .V4                5.217    0.675    7.726    0.000    5.217    0.518
   .V5                3.383    0.508    6.655    0.000    3.383    0.396
   .V6                6.116    0.677    9.032    0.000    6.116    0.841
   .V7                5.358    0.741    7.231    0.000    5.358    0.626
   .V8                5.620    0.663    8.480    0.000    5.620    0.799
   .V9                3.979    0.623    6.385    0.000    3.979    0.545
   .V10               5.376    0.707    7.603    0.000    5.376    0.668
   .V11               8.162    0.874    9.337    0.000    8.162    0.995
    verbal_IQ         5.090    0.899    5.659    0.000    1.000    1.000
    Performance_IQ    0.782    0.470    1.662    0.097    1.000    1.000

R-Square:
                   Estimate
    V1                0.604
    V2                0.505
    V3                0.323
    V4                0.482
    V5                0.604
    V6                0.159
    V7                0.374
    V8                0.201
    V9                0.455
    V10               0.332
    V11               0.005

可以看出X11的因素载荷是不显著的，且标准化的载荷值只有0.070。可以考虑删除X11

修正后的第二次CFA

比较模型拟合指数

模型2是在模型1的基础上增加了参数，两个模型呈嵌套关系，可以进行拟合程度比较。

1
anova(fit1, fit2)
1
2
3
4
5
Chi-Squared Difference Test

     Df    AIC    BIC  Chisq Chisq diff   RMSEA Df diff Pr(>Chisq)   
fit2 42 9043.6 9154.4 60.642                                         
fit1 43 9051.6 9159.2 70.640      9.998 0.22675       1   0.001567 **

可以看出两个模型的卡方值的差值Chisq diff为9.998，自由度的差值为1，表明两个模型的差异显著。模型二的拟合指数AIC、BIC、RMSEA、CFI、TLI优于模型1。

修正后的第三次CFA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 修正模型
model3 <- '
  # 定义潜变量 verbal_IQ
  verbal_IQ =~ V1 + V2 + V3 + V4 + V5 + V6
  
  # 定义潜变量 Performance_IQ
  Performance_IQ =~ V2 + V7 + V8 + V9 + V10
  
  # 显式请求截距
  V1 ~1
  V2 ~1
  V3 ~1
  V4 ~1
  V5 ~1
  V6 ~1
  V7 ~1
  V8 ~1
  V9 ~1
  V10 ~1
'

fit3 <- cfa(model3, data=data)
summary(fit3, fit.measures = TRUE, standardized=TRUE, rsquare = TRUE)

# 创建可视化
semPaths(fit3, whatLabels="est", layout="tree", edge.label.cex=0.8, node.label.cex=0.9)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
Model Test User Model:
                                                      
  Test statistic                                45.276
  Degrees of freedom                                33
  P-value (Chi-square)                           0.075

Model Test Baseline Model:

  Test statistic                               503.222
  Degrees of freedom                                45
  P-value                                        0.000

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.973
  Tucker-Lewis Index (TLI)                       0.963

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -4054.684
  Loglikelihood unrestricted model (H1)      -4032.046
                                                      
  Akaike (AIC)                                8173.368
  Bayesian (BIC)                              8274.642
  Sample-size adjusted Bayesian (SABIC)       8173.308

Root Mean Square Error of Approximation:

  RMSEA                                          0.046
  90 Percent confidence interval - lower         0.000
  90 Percent confidence interval - upper         0.077
  P-value H_0: RMSEA <= 0.050                    0.549
  P-value H_0: RMSEA >= 0.080                    0.033

Standardized Root Mean Square Residual:

  SRMR                                           0.045
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
Latent Variables:
                    Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  verbal_IQ =~                                                           
    V1                 1.000                               2.256    0.777
    V2                 0.661    0.118    5.608    0.000    1.491    0.504
    V3                 0.579    0.082    7.099    0.000    1.306    0.568
    V4                 0.977    0.112    8.755    0.000    2.206    0.695
    V5                 1.007    0.103    9.738    0.000    2.273    0.777
    V6                 0.476    0.097    4.916    0.000    1.074    0.398
  Performance_IQ =~                                                      
    V2                 1.000                               0.885    0.299
    V7                 2.041    0.661    3.088    0.002    1.807    0.618
    V8                 1.340    0.468    2.863    0.004    1.186    0.447
    V9                 2.045    0.657    3.114    0.002    1.811    0.670
    V10                1.843    0.604    3.051    0.002    1.632    0.575

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  verbal_IQ ~~                                                          
    Performance_IQ    1.064    0.381    2.797    0.005    0.533    0.533

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .V1                9.497    0.220   43.264    0.000    9.497    3.270
   .V2               10.000    0.224   44.740    0.000   10.000    3.382
   .V3                9.000    0.174   51.758    0.000    9.000    3.913
   .V4               10.611    0.240   44.220    0.000   10.611    3.343
   .V5               10.703    0.221   48.416    0.000   10.703    3.660
   .V6                8.731    0.204   42.837    0.000    8.731    3.238
   .V7               10.680    0.221   48.288    0.000   10.680    3.650
   .V8               10.371    0.200   51.734    0.000   10.371    3.911
   .V9               10.314    0.204   50.496    0.000   10.314    3.817
   .V10              10.903    0.214   50.860    0.000   10.903    3.845

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .V1                3.342    0.502    6.662    0.000    3.342    0.396
   .V2                4.329    0.554    7.815    0.000    4.329    0.495
   .V3                3.585    0.420    8.534    0.000    3.585    0.677
   .V4                5.213    0.675    7.724    0.000    5.213    0.517
   .V5                3.385    0.508    6.658    0.000    3.385    0.396
   .V6                6.117    0.677    9.032    0.000    6.117    0.841
   .V7                5.295    0.740    7.156    0.000    5.295    0.619
   .V8                5.626    0.663    8.482    0.000    5.626    0.800
   .V9                4.022    0.624    6.445    0.000    4.022    0.551
   .V10               5.379    0.708    7.602    0.000    5.379    0.669
    verbal_IQ         5.091    0.899    5.660    0.000    1.000    1.000
    Performance_IQ    0.784    0.471    1.665    0.096    1.000    1.000

R-Square:
                   Estimate
    V1                0.604
    V2                0.505
    V3                0.323
    V4                0.483
    V5                0.604
    V6                0.159
    V7                0.381
    V8                0.200
    V9                0.449
    V10               0.331

修正后的第三次CFA

比较模型拟合指数

1
2
3
4
5
6
Chi-Squared Difference Test

     Df    AIC    BIC  Chisq Chisq diff    RMSEA Df diff Pr(>Chisq)   
fit3 33 8173.4 8274.6 45.276                                          
fit2 42 9043.6 9154.4 60.642     15.365 0.063572       9   0.081379 . 
fit1 43 9051.6 9159.2 70.640      9.998 0.226753       1   0.001567 **

模型三与模型二保焊的变量不同，不具有嵌套关系。只需要参考拟合指数AIC、BIC、RMSEA、CFI、TLI，表明模型三优于模型二。

等价性检验

对不同性别的测验等价性进行检验

1
2
3
4
analysis_data_withgender$V14 <- factor(analysis_data_withgender$V14, levels = c(0, 1), labels = c("male", "female"))

# 查看性别分布
table(analysis_data_withgender$V14)

使用最终确定的模型三作为等价性检验模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
model3 <- '
  # 定义潜变量 verbal_
IQ
  verbal_IQ =~ V1 + V2 + V3 + V4 + V5 + V6
  
  # 定义潜变量 Performance_IQ
  Performance_IQ =~ V2 + V7 + V8 + V9 + V10
  
  # 显式请求截距
  V1 ~1
  V2 ~1
  V3 ~1
  V4 ~1
  V5 ~1
  V6 ~1
  V7 ~1
  V8 ~1
  V9 ~1
  V10 ~1
'

不同性别分别拟合模型

1
2
3
4
5
6
7
8
9
10
11
# 分别提取男性和女性的数据
data_male <- subset(data, V14 == "male")
data_female <- subset(data, V14 == "female")

# 对男性数据拟合模型
fit_male <- cfa(model3, data = data_male)
summary(fit_male, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE)

# 对女性数据拟合模型
fit_female <- cfa(model3, data = data_female)
summary(fit_female, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
> summary(fit_male, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE)

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.910
  Tucker-Lewis Index (TLI)                       0.877

Root Mean Square Error of Approximation:

  RMSEA                                          0.081
  90 Percent confidence interval - lower         0.033
  90 Percent confidence interval - upper         0.122
  P-value H_0: RMSEA <= 0.050                    0.121
  P-value H_0: RMSEA >= 0.080                    0.546
  
> summary(fit_female, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE)

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    1.000
  Tucker-Lewis Index (TLI)                       1.030

Root Mean Square Error of Approximation:

  RMSEA                                          0.000
  90 Percent confidence interval - lower         0.000
  90 Percent confidence interval - upper         0.058
  P-value H_0: RMSEA <= 0.050                    0.920
  P-value H_0: RMSEA >= 0.080                    0.008

可以看出男生组RMSEA为0.081，CFI值为0.910，TLI值为0.877；女生组RMSEA为0.000，CFI值为1.000，TLI值为1.030，表明两组模型都拟合良好

因素模式相同模型(基线模型)

1
2
3
# 配置等价模型
configural_model <- cfa(model3, data=data, group="V14")
summary(configural_model, fit.measures=TRUE, standardized=TRUE, rsquare = TRUE)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
Model Test User Model:
                                                      
  Test statistic                                79.129
  Degrees of freedom                                66
  P-value (Chi-square)                           0.129
  Test statistic for each group:
    female                                      27.457
    male                                        51.672

Model Test Baseline Model:

  Test statistic                               548.746
  Degrees of freedom                                90
  P-value                                        0.000

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.971
  Tucker-Lewis Index (TLI)                       0.961

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -4044.360
  Loglikelihood unrestricted model (H1)      -4004.796
                                                      
  Akaike (AIC)                                8216.720
  Bayesian (BIC)                              8419.266
  Sample-size adjusted Bayesian (SABIC)       8216.598

Root Mean Square Error of Approximation:

  RMSEA                                          0.048
  90 Percent confidence interval - lower         0.000
  90 Percent confidence interval - upper         0.083
  P-value H_0: RMSEA <= 0.050                    0.516
  P-value H_0: RMSEA >= 0.080                    0.068

Standardized Root Mean Square Residual:

  SRMR                                           0.057

可以看出RMSEA值为0.048，CFI的值为0.971，TLI的值为0.961，表明模型拟合较好。该模型作为基线模型，用于检验其他等价性条件是否满足。

因素载荷等价模型(弱等价性)

不同组的观测变量与对应的潜变量之间的因素载荷的值是相等的

1
2
3
# 度量等价
metric_model <- cfa(model3, data=analysis_data_withgender, group="V14", group.equal="loadings")
summary(metric_model, fit.measures=TRUE, standardized=TRUE, rsquare = TRUE)
1
2
3
4
5
6
7
> anova(configural_model, metric_model)

Chi-Squared Difference Test

                 Df    AIC    BIC  Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
configural_model 66 8216.7 8419.3 79.129                                    
metric_model     75 8205.9 8380.0 86.297     7.1688     0       9     0.6196

弱等价性模型嵌套于基线模型，可以使用嵌套模型的比较方法。

可以看出两个模型的卡方值的差值Chisq diff为7.1688，自由度的差值Df diff为9，表明两个模型的卡方差异不显著。可以接受弱等价模型，即认为不同性别之间满足因素载荷等价条件。

截距等价性模型(强等价性)

不同组的观测变量的截距相等

1
2
3
# 截距等价
scalar_model <- cfa(model3, data=analysis_data_withgender, group="V14", group.equal=c("loadings", "intercepts"))
summary(scalar_model, fit.measures=TRUE, standardized=TRUE, rsquare = TRUE)
1
2
3
4
5
6
7
8
> anova(configural_model, metric_model, scalar_model)

Chi-Squared Difference Test

                 Df    AIC    BIC  Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
configural_model 66 8216.7 8419.3 79.129                                    
metric_model     75 8205.9 8380.0 86.297     7.1688     0       9     0.6196
scalar_model     83 8193.3 8342.0 89.687     3.3898     0       8     0.9076

强等价性模型嵌套于弱等价性模型，可以使用嵌套模型的比较方法。

可以看出两个模型的卡方值的差值Chisq diff为3.3898，自由度的差值Df diff为8，表明两个模型的卡方差异不显著。可以接受强等价模型，即认为不同性别之间满足截距等价条件。

误差方差等价模型

假定来自不同组的误差方差相等

1
2
3
# 误差方差等价
error_variance_model <- cfa(model3, data=analysis_data_withgender, group="V14", group.equal=c("loadings", "intercepts", "residuals"))
summary(error_variance_model, fit.measures=TRUE, standardized=TRUE, rsquare = TRUE)
1
2
3
4
5
6
7
8
9
> anova(configural_model, metric_model, scalar_model, error_variance_model)

Chi-Squared Difference Test

                     Df    AIC    BIC  Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
configural_model     66 8216.7 8419.3 79.129                                    
metric_model         75 8205.9 8380.0 86.297     7.1688     0       9     0.6196
scalar_model         83 8193.3 8342.0 89.687     3.3898     0       8     0.9076
error_variance_model 93 8178.4 8295.5 94.812     5.1252     0      10     0.8827

误差方差等价模型嵌套于强等价性模型，可以使用嵌套模型的比较方法。

可以看出两个模型的卡方值的差值Chisq diff为5.1252，自由度的差值Df diff为10，表明两个模型的卡方差异不显著。可以接受误差方差等价模型，即认为不同性别之间满足误差方差等价条件。

潜变量方差等价模型

假定来自不同组的误差方差相等，不同组的误差协方差相等

1
2
3
# 潜变量方差等价
latent_variance_model <- cfa(model3, data=analysis_data_withgender, group="V14", group.equal=c("loadings", "intercepts", "residuals", "lv.variances"))
summary(latent_variance_model, fit.measures=TRUE, standardized=TRUE, rsquare = TRUE)
1
2
3
4
5
6
7
8
9
10
> anova(configural_model, metric_model, scalar_model, error_variance_model, latent_variance_model)

Chi-Squared Difference Test

                      Df    AIC    BIC  Chisq Chisq diff    RMSEA Df diff Pr(>Chisq)
configural_model      66 8216.7 8419.3 79.129                                       
metric_model          75 8205.9 8380.0 86.297     7.1688 0.000000       9     0.6196
scalar_model          83 8193.3 8342.0 89.687     3.3898 0.000000       8     0.9076
error_variance_model  93 8178.4 8295.5 94.812     5.1252 0.000000      10     0.8827
latent_variance_model 95 8177.7 8288.5 98.131     3.3185 0.086801       2     0.1903

潜变量方差等价模型嵌套于误差方差等价模型，可以使用嵌套模型的比较方法。

可以看出两个模型的卡方值的差值Chisq diff为3.3185，自由度的差值Df diff为2，表明两个模型的卡方差异不显著。可以接受潜变量方差等价模型，即认为不同性别之间满足潜变量方差等价条件。

潜变量协方差矩阵等价模型

1
2
3
# 潜变量协方差等价
latent_covariance_model <- cfa(model3, data=analysis_data_withgender, group="V14", group.equal=c("loadings", "intercepts", "residuals", "lv.variances", "lv.covariances"))
summary(latent_covariance_model, fit.measures=TRUE, standardized=TRUE, rsquare = TRUE)
1
2
3
4
5
6
7
8
9
10
11
> anova(configural_model, metric_model, scalar_model, error_variance_model, latent_variance_model, latent_covariance_model)

Chi-Squared Difference Test

                        Df    AIC    BIC  Chisq Chisq diff    RMSEA Df diff Pr(>Chisq)
configural_model        66 8216.7 8419.3 79.129                                       
metric_model            75 8205.9 8380.0 86.297     7.1688 0.000000       9     0.6196
scalar_model            83 8193.3 8342.0 89.687     3.3898 0.000000       8     0.9076
error_variance_model    93 8178.4 8295.5 94.812     5.1252 0.000000      10     0.8827
latent_variance_model   95 8177.7 8288.5 98.131     3.3185 0.086801       2     0.1903
latent_covariance_model 96 8176.8 8284.4 99.187     1.0564 0.025385       1     0.3040

潜变量协方差等价模型嵌套于潜变量方差等价模型，可以使用嵌套模型的比较方法。

可以看出两个模型的卡方值的差值Chisq diff为1.0564，自由度的差值Df diff为1，表明两个模型的卡方差异不显著。可以接受潜变量协方差等价模型，即认为不同性别之间满足潜变量协方差等价条件。

潜变量的均值等价模型

1
2
3
# 潜变量均值等价
latent_mean_model <- cfa(model3, data=analysis_data_withgender, group="V14", group.equal=c("loadings", "intercepts", "residuals", "lv.variances", "lv.covariances", "means"))
summary(latent_mean_model, fit.measures=TRUE, standardized=TRUE, rsquare = TRUE)
1
2
3
4
5
6
7
8
9
10
11
12
> anova(configural_model, metric_model, scalar_model, error_variance_model, latent_variance_model, latent_covariance_model, latent_mean_model)

Chi-Squared Difference Test

                        Df    AIC    BIC  Chisq Chisq diff    RMSEA Df diff Pr(>Chisq)
configural_model        66 8216.7 8419.3 79.129                                       
metric_model            75 8205.9 8380.0 86.297     7.1688 0.000000       9     0.6196
scalar_model            83 8193.3 8342.0 89.687     3.3898 0.000000       8     0.9076
error_variance_model    93 8178.4 8295.5 94.812     5.1252 0.000000      10     0.8827
latent_variance_model   95 8177.7 8288.5 98.131     3.3185 0.086801       2     0.1903
latent_covariance_model 96 8176.8 8284.4 99.187     1.0564 0.025385       1     0.3040
latent_mean_model       98 8173.4 8274.6 99.777     0.5901 0.000000       2     0.7445

潜变量均值等价模型嵌套于潜变量协方差等价，可以使用嵌套模型的比较方法。

可以看出两个模型的卡方值的差值Chisq diff为0.5901，自由度的差值Df diff为2，表明两个模型的卡方差异不显著。可以接受潜变量均值等价模型，即认为不同性别之间满足潜变量均值等价条件。

路径分析

导入包与数据

1
2
3
4
5
6
7
8
9
10
11
12
# 导入包
library(psych)
library(lavaan)
library(tidySEM)

# 导入数据
setwd("/Users/nanxu/研究生课程作业/心理统计/课件数据/9第九章 路径分析/")
data <- read.table("./9_1_dataPA.dat", header = FALSE, sep = "", na.strings = "NA")

# 查看数据
names(data)
dim(data)

数据介绍

1
2
3
# 描述数据
summary(data)
# describe(data)
1
2
3
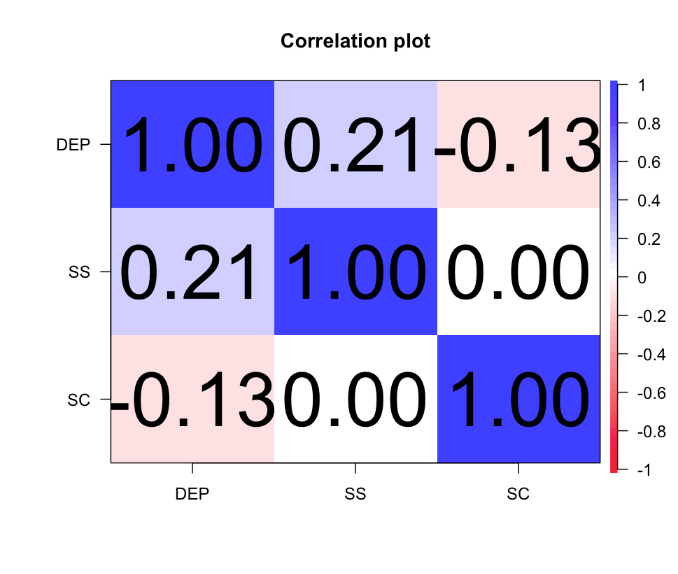
# 计算相关系数矩阵
cor_matrix <- cor(data, use="complete.obs")
cor.plot(cor_matrix)

相关矩阵

饱和的递归模型

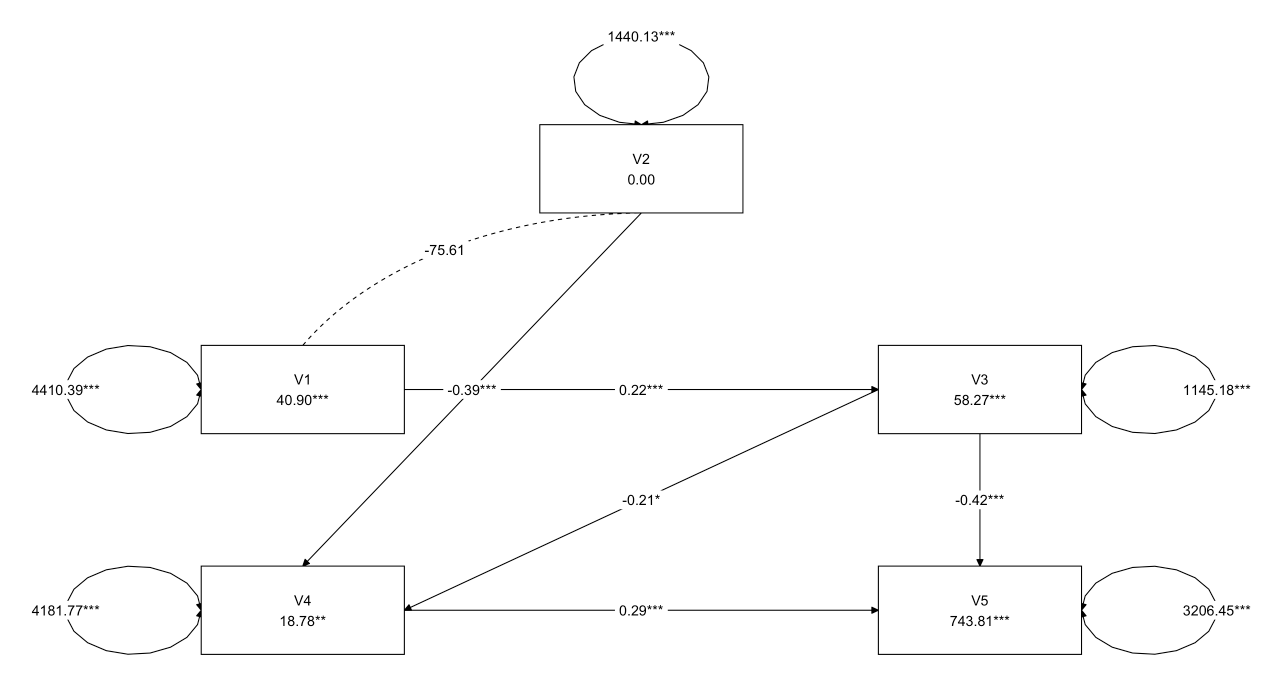
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 定义模型
model1 <- '
  # 因果关系
  V3 ~ V1 + V2
  V4 ~ V1 + V2 + V3
  V5 ~ V1 + V2 + V3 + V4

  # 协方差
  V1 ~~ V2 

  # 指定残差
  V3 ~~ V3
  V4 ~~ V4
  V5 ~~ V5
  
  # 显式请求截距
  V3 ~1
  V4 ~1
  V5 ~1
'

# 拟合模型
fit1 <- sem(model1, data=data)
summary(fit1, fit.measures=TRUE, standardized=TRUE)

# 可视化
layout_matrix <- matrix(NA, nrow = 3, ncol = 3, dimnames = list(NULL, NULL))
layout_matrix[1, 2] <- "V2"
layout_matrix[2, 1] <- "V1"
layout_matrix[2, 3] <- "V3"
layout_matrix[3, 1] <- "V4"
layout_matrix[3, 3] <- "V5"
graph_sem(fit1, layout = layout_matrix, text_size = 5)

饱和递归模型

模型拟合结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
Model Test User Model:
                                                      
  Test statistic                                 0.000
  Degrees of freedom                                 0

Model Test Baseline Model:

  Test statistic                               165.893
  Degrees of freedom                                10
  P-value                                        0.000

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    1.000
  Tucker-Lewis Index (TLI)                       1.000

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -9938.865
  Loglikelihood unrestricted model (H1)      -9938.865
                                                      
  Akaike (AIC)                               19907.729
  Bayesian (BIC)                             19966.553
  Sample-size adjusted Bayesian (SABIC)      19918.962

Root Mean Square Error of Approximation:

  RMSEA                                          0.000
  90 Percent confidence interval - lower         0.000
  90 Percent confidence interval - upper         0.000
  P-value H_0: RMSEA <= 0.050                       NA
  P-value H_0: RMSEA >= 0.080                       NA

Standardized Root Mean Square Residual:

  SRMR                                           0.000

参数估计结果与标准化参数估计结果

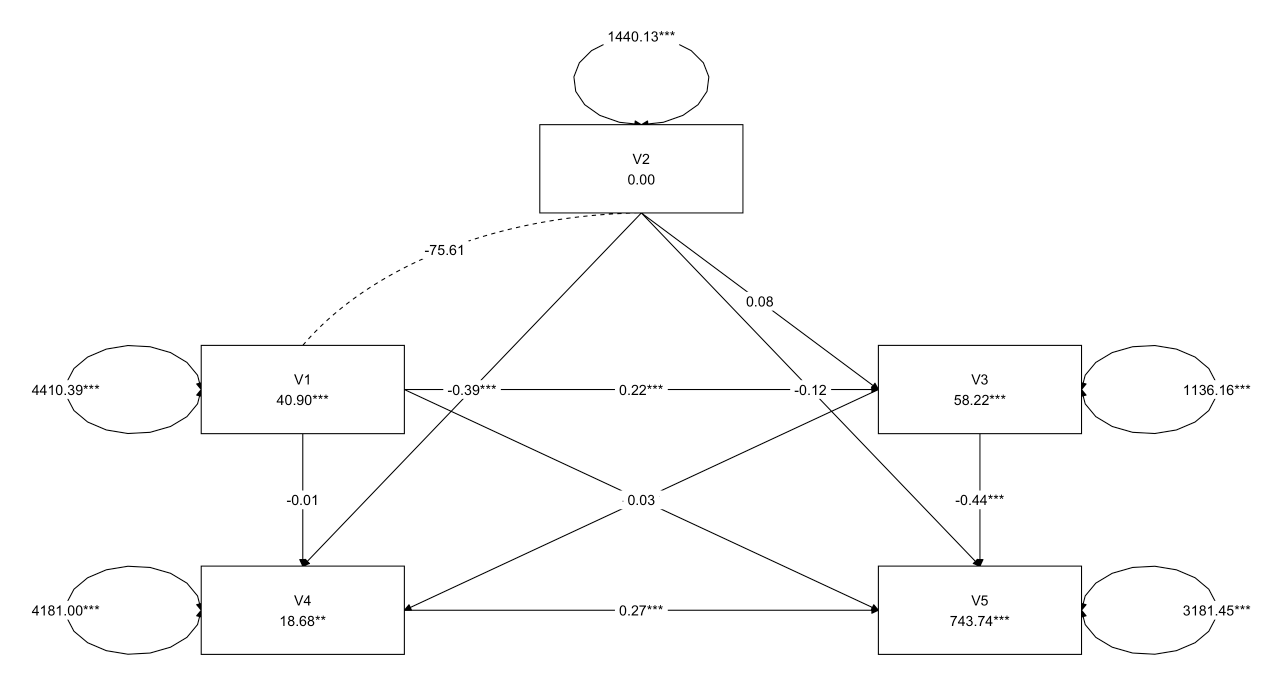
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
Regressions:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  V3 ~                                                                  
    V1                0.217    0.026    8.260    0.000    0.217    0.392
    V2                0.079    0.046    1.721    0.085    0.079    0.082
  V4 ~                                                                  
    V1               -0.014    0.055   -0.261    0.794   -0.014   -0.014
    V2               -0.393    0.089   -4.433    0.000   -0.393   -0.223
    V3               -0.198    0.099   -1.995    0.046   -0.198   -0.109
  V5 ~                                                                  
    V1                0.032    0.048    0.663    0.507    0.032    0.034
    V2               -0.122    0.079   -1.533    0.125   -0.122   -0.074
    V3               -0.442    0.087   -5.071    0.000   -0.442   -0.260
    V4                0.271    0.045    6.005    0.000    0.271    0.291

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  V1 ~~                                                                 
    V2              -75.607  130.551   -0.579    0.562  -75.607   -0.030

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .V3               58.217    2.050   28.399    0.000   58.217    1.584
   .V4               18.685    6.993    2.672    0.008   18.685    0.279
   .V5              743.742    6.158  120.772    0.000  743.742   11.916
    V1               40.900    3.439   11.894    0.000   40.900    0.616
    V2                0.000    1.965    0.000    1.000    0.000    0.000

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .V3             1136.158   83.195   13.657    0.000 1136.158    0.841
   .V4             4181.001  306.155   13.657    0.000 4181.001    0.934
   .V5             3181.454  232.963   13.657    0.000 3181.454    0.817
    V1             4410.394  322.952   13.657    0.000 4410.394    1.000
    V2             1440.129  105.454   13.657    0.000 1440.129    1.000

可以看出V1 ~ V4、V2 ~ V3、V1 ~ V5、V2 ~ V5路径不显著，可以考虑后续模型修正。

间接因果效应计算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
# 计算间接效应
model2 <- '
  # 因果关系
  V3 ~ c1*V1 + c2*V2
  V4 ~ b1*V1 + b2*V2 + b3*V3
  V5 ~ a1*V1 + a2*V2 + a3*V3 + a4*V4

  # 协方差
  V1 ~~ V2 

  # 指定残差
  V3 ~~ e3*V3
  V4 ~~ e4*V4
  V5 ~~ e5*V5

  # 显式请求截距
  V3 ~1
  V4 ~1
  V5 ~1
  
  # 计算间接效应
  # 间接效应: V1到V4通过V3
  ind_V1_V4 := c1 * b3
  # 间接效应: V1到V5通过V3和V4
  ind_V1_V5 := a4 * (ind_V1_V4 + b1) + a3 * c1
  # 间接效应: V2到V4通过V3
  ind_V2_V4 := c2 * b3
  # 间接效应: V2到V5通过V3和V4
  ind_V2_V5 := a4 * (ind_V2_V4 + b2) + a3 * c2
  # 间接效应: V3到V5通过V4
  ind_V3_V5 := b3 * a4

  # 计算总效应
  # 总效应: V1到V4
  total_V1_V4 := b1 + ind_V1_V4
  # 总效应: V1到V5
  total_V1_V5 := a1 + ind_V1_V5
  # 总效应: V2到V4
  total_V2_V4 := b2 + ind_V2_V4
  # 总效应: V2到V5
  total_V2_V5 := a2 + ind_V2_V5
  # 总效应: V3到V5
  total_V3_V5 := a3 + ind_V3_V5
'

# 拟合模型
fit2 <- sem(model2, data=data)
summary(fit2, fit.measures=TRUE, standardized=TRUE)

间接效应与直接效应的估计值与标准化估计值

1
2
3
4
5
6
7
8
9
10
11
12
Defined Parameters:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    ind_V1_V4        -0.043    0.022   -1.939    0.052   -0.043   -0.043
    ind_V1_V5        -0.112    0.027   -4.181    0.000   -0.112   -0.119
    ind_V2_V4        -0.016    0.012   -1.303    0.192   -0.016   -0.009
    ind_V2_V5        -0.146    0.038   -3.822    0.000   -0.146   -0.089
    ind_V3_V5        -0.054    0.028   -1.893    0.058   -0.054   -0.032
    total_V1_V4      -0.057    0.051   -1.132    0.258   -0.057   -0.057
    total_V1_V5      -0.080    0.048   -1.666    0.096   -0.080   -0.085
    total_V2_V4      -0.409    0.089   -4.604    0.000   -0.409   -0.232
    total_V2_V5      -0.267    0.084   -3.191    0.001   -0.267   -0.163
    total_V3_V5      -0.496    0.091   -5.461    0.000   -0.496   -0.292

非饱和的递归模型

删去V2到V3路径以及V1到V4路径

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
# 非饱和递归模型
model3 <- '
  # 因果关系
  V3 ~ c1*V1
  V4 ~ b2*V2 + b3*V3
  V5 ~ a1*V1 + a2*V2 + a3*V3 + a4*V4

  # 协方差
  V1 ~~ V2 

  # 指定残差
  V3 ~~ e3*V3
  V4 ~~ e4*V4
  V5 ~~ e5*V5
  
  # 显式请求截距
  V3 ~1
  V4 ~1
  V5 ~1
  
  # 计算间接效应
  # 间接效应: V1到V4通过V3
  ind_V1_V4 := c1 * b3
  # 间接效应: V1到V5通过V3和V4
  ind_V1_V5 := c1 * b3 * a4 + c1 * a3
  # 间接效应: V2到V5通过V4
  ind_V2_V5 := b2 * a4
  # 间接效应: V3到V5通过V4
  ind_V3_V5 := b3 * a4

  # 计算总效应
  # 总效应: V1到V5
  total_V1_V5 := a1 + ind_V1_V5
  # 总效应: V2到V5
  total_V2_V5 := a2 + ind_V2_V5
  # 总效应: V3到V5
  total_V3_V5 := a3 + ind_V3_V5
'

fit3 <- sem(model3, data=data)
summary(fit3, fit.measures=TRUE, standardized=TRUE, estimates=TRUE)

# 可视化
layout_matrix <- matrix(NA, nrow = 3, ncol = 3, dimnames = list(NULL, NULL))
layout_matrix[1, 2] <- "V2"
layout_matrix[2, 1] <- "V1"
layout_matrix[2, 3] <- "V3"
layout_matrix[3, 1] <- "V4"
layout_matrix[3, 3] <- "V5"
graph_sem(fit3, layout = layout_matrix, text_size = 5)

非饱和递归模型

模型拟合结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
Model Test User Model:
                                                      
  Test statistic                                 3.019
  Degrees of freedom                                 2
  P-value (Chi-square)                           0.221

Model Test Baseline Model:

  Test statistic                               165.893
  Degrees of freedom                                10
  P-value                                        0.000

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.993
  Tucker-Lewis Index (TLI)                       0.967

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -9940.374
  Loglikelihood unrestricted model (H1)      -9938.865
                                                      
  Akaike (AIC)                               19916.748
  Bayesian (BIC)                             19987.337
  Sample-size adjusted Bayesian (SABIC)      19930.228

Root Mean Square Error of Approximation:

  RMSEA                                          0.037
  90 Percent confidence interval - lower         0.000
  90 Percent confidence interval - upper         0.116
  P-value H_0: RMSEA <= 0.050                    0.493
  P-value H_0: RMSEA >= 0.080                    0.237

Standardized Root Mean Square Residual:

  SRMR                                           0.020

参数估计结果与标准化参数估计结果

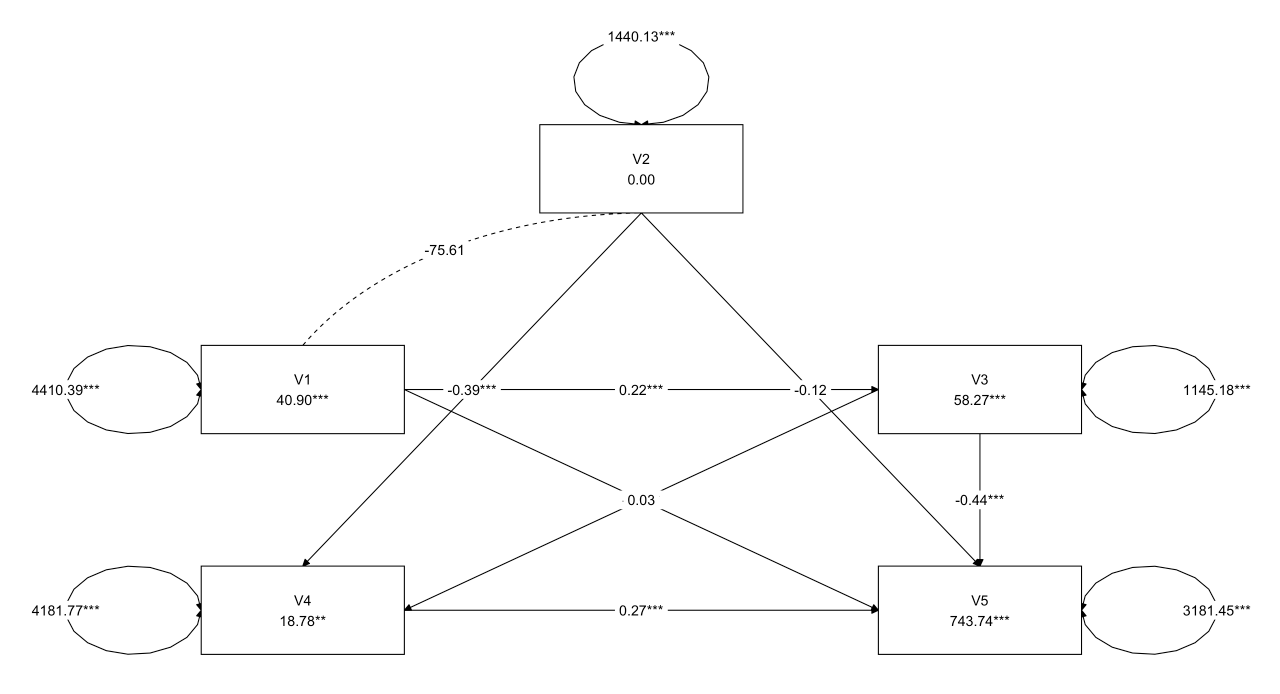
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
Regressions:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  V3 ~                                                                  
    V1        (c1)    0.216    0.026    8.180    0.000    0.216    0.390
  V4 ~                                                                  
    V2        (b2)   -0.391    0.088   -4.436    0.000   -0.391   -0.222
    V3        (b3)   -0.208    0.091   -2.287    0.022   -0.208   -0.115
  V5 ~                                                                  
    V1        (a1)    0.032    0.048    0.664    0.507    0.032    0.034
    V2        (a2)   -0.122    0.079   -1.539    0.124   -0.122   -0.074
    V3        (a3)   -0.442    0.087   -5.088    0.000   -0.442   -0.261
    V4        (a4)    0.271    0.045    6.006    0.000    0.271    0.291

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  V1 ~~                                                                 
    V2              -75.607  130.551   -0.579    0.562  -75.607   -0.030

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .V3               58.273    2.058   28.318    0.000   58.273    1.586
   .V4               18.783    6.971    2.695    0.007   18.783    0.281
   .V5              743.742    6.146  121.004    0.000  743.742   11.954
    V1               40.900    3.439   11.894    0.000   40.900    0.616
    V2                0.000    1.965    0.000    1.000    0.000    0.000

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .V3        (e3) 1145.182   83.856   13.657    0.000 1145.182    0.848
   .V4        (e4) 4181.767  306.211   13.657    0.000 4181.767    0.938
   .V5        (e5) 3181.453  232.963   13.657    0.000 3181.453    0.822
    V1             4410.394  322.952   13.657    0.000 4410.394    1.000
    V2             1440.129  105.454   13.657    0.000 1440.129    1.000

Defined Parameters:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    ind_V1_V4        -0.045    0.020   -2.203    0.028   -0.045   -0.045
    ind_V1_V5        -0.108    0.023   -4.593    0.000   -0.108   -0.115
    ind_V2_V5        -0.106    0.030   -3.568    0.000   -0.106   -0.065
    ind_V3_V5        -0.057    0.026   -2.137    0.033   -0.057   -0.033
    total_V1_V5      -0.076    0.046   -1.640    0.101   -0.076   -0.081
    total_V2_V5      -0.228    0.081   -2.824    0.005   -0.228   -0.139
    total_V3_V5      -0.498    0.090   -5.550    0.000   -0.498   -0.294

可以看出V1 ~ V5、V2 ~ V5路径不显著，可以考虑后续模型修正。

1
2
3
4
5
6
7
> anova(fit2, fit3)

Chi-Squared Difference Test

     Df   AIC   BIC Chisq Chisq diff    RMSEA Df diff Pr(>Chisq)
fit2  0 19918 19996 0.000                                       
fit3  2 19917 19987 3.019     3.0189 0.036958       2      0.221

非饱和模型的卡方值Chisq为3.019，p值Pr(>Chisq)为0.221，即在0.05水平上不显著

但是RMSEA、CFI、TLI都达到了模型良好拟合的判断标准，而且相比饱和模型的拟合指数相比变化量更小，表明删去路径后非饱和模型能比饱和模型能够更好地拟合数据，统计上可以接受零假设，因此对原饱和模型进行修正，用该非饱和模型进行替代

删去V1到V5路径以及V2到V5路径

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
# 修正模型
model4 <- '
  # 因果关系
  V3 ~ c1*V1
  V4 ~ b2*V2 + b3*V3
  V5 ~ a3*V3 + a4*V4

  # 协方差
  V1 ~~ V2 

  # 指定残差
  V3 ~~ e3*V3
  V4 ~~ e4*V4
  V5 ~~ e5*V5
  
  # 显式请求截距
  V3 ~1
  V4 ~1
  V5 ~1

  # 计算间接效应
  # 间接效应: V1到V4通过V3
  ind_V1_V4 := c1*b3
  # 间接效应: V1到V5通过V3和V4
  ind_V1_V5 := c1 * b3 * a4 + c1 * a3
  # 间接效应: V2到V5通过V4
  ind_V2_V5 := b2 * a4
  # 间接效应: V3到V5通过V4
  ind_V3_V5 := b3 * a4

  # 计算总效应
  # 总效应: V3到V5
  total_V3_V5 := a3 + ind_V3_V5
'

fit4 <- sem(model4, data=data)
summary(fit4, fit.measures=TRUE, standardized=TRUE, estimates=TRUE)

# 可视化
layout_matrix <- matrix(NA, nrow = 3, ncol = 3, dimnames = list(NULL, NULL))
layout_matrix[1, 2] <- "V2"
layout_matrix[2, 1] <- "V1"
layout_matrix[2, 3] <- "V3"
layout_matrix[3, 1] <- "V4"
layout_matrix[3, 3] <- "V5"
graph_sem(fit4, layout = layout_matrix, text_size = 5)

非饱和模型

模型拟合结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
Model Test User Model:
                                                      
  Test statistic                                 5.938
  Degrees of freedom                                 4
  P-value (Chi-square)                           0.204

Model Test Baseline Model:

  Test statistic                               165.893
  Degrees of freedom                                10
  P-value                                        0.000

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.988
  Tucker-Lewis Index (TLI)                       0.969

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -9941.834
  Loglikelihood unrestricted model (H1)      -9938.865
                                                      
  Akaike (AIC)                               19915.667
  Bayesian (BIC)                             19978.412
  Sample-size adjusted Bayesian (SABIC)      19927.649

Root Mean Square Error of Approximation:

  RMSEA                                          0.036
  90 Percent confidence interval - lower         0.000
  90 Percent confidence interval - upper         0.092
  P-value H_0: RMSEA <= 0.050                    0.582
  P-value H_0: RMSEA >= 0.080                    0.113

Standardized Root Mean Square Residual:

  SRMR                                           0.029

参数估计结果与标准化参数估计结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
Regressions:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  V3 ~                                                                  
    V1        (c1)    0.216    0.026    8.180    0.000    0.216    0.390
  V4 ~                                                                  
    V2        (b2)   -0.391    0.088   -4.436    0.000   -0.391   -0.222
    V3        (b3)   -0.208    0.091   -2.287    0.022   -0.208   -0.115
  V5 ~                                                                  
    V3        (a3)   -0.424    0.080   -5.287    0.000   -0.424   -0.250
    V4        (a4)    0.287    0.044    6.489    0.000    0.287    0.307

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  V1 ~~                                                                 
    V2              -75.607  130.551   -0.579    0.562  -75.607   -0.030

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .V3               58.273    2.058   28.318    0.000   58.273    1.586
   .V4               18.783    6.971    2.695    0.007   18.783    0.281
   .V5              743.808    6.158  120.790    0.000  743.808   11.936
    V1               40.900    3.439   11.894    0.000   40.900    0.616
    V2                0.000    1.965    0.000    1.000    0.000    0.000

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .V3        (e3) 1145.182   83.856   13.657    0.000 1145.182    0.848
   .V4        (e4) 4181.767  306.211   13.657    0.000 4181.767    0.938
   .V5        (e5) 3206.449  234.793   13.657    0.000 3206.449    0.826
    V1             4410.394  322.952   13.657    0.000 4410.394    1.000
    V2             1440.129  105.454   13.657    0.000 1440.129    1.000

Defined Parameters:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    ind_V1_V4        -0.045    0.020   -2.203    0.028   -0.045   -0.045
    ind_V1_V5        -0.105    0.022   -4.714    0.000   -0.105   -0.111
    ind_V2_V5        -0.112    0.031   -3.662    0.000   -0.112   -0.068
    ind_V3_V5        -0.060    0.028   -2.157    0.031   -0.060   -0.035
    total_V3_V5      -0.484    0.084   -5.768    0.000   -0.484   -0.286
1
2
3
4
5
6
7
8
> anova(fit2, fit3, fit4)

Chi-Squared Difference Test

     Df   AIC   BIC  Chisq Chisq diff    RMSEA Df diff Pr(>Chisq)
fit2  0 19918 19996 0.0000                                       
fit3  2 19917 19987 3.0190     3.0189 0.036958       2     0.2210
fit4  4 19916 19978 5.9377     2.9188 0.035094       2     0.2324

结构方程模型

导入包与数据

1
2
3
4
5
6
7
8
9
10
11
# 导入包
library(lavaan)
library(tidySEM)

# 导入数据
setwd("/Users/nanxu/研究生课程作业/心理统计/课件数据/10第十章 结构方程模型/")
data <- read.table("./10_1.dat", header = FALSE, sep = "", na.strings = "NA")

# 查看数据
names(data)
dim(data)

数据介绍

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 数据名称
# work1 -- V1
# work2 -- V2
# ee1 -- V3
# ee2 -- V4
# ee3 -- V5
# dpl1 -- V6
# dpl2 -- V7
# pa1 -- V8
# pa2 -- V9
# pa3 -- V10
# Gender -- V11

# 重命名数据集中的变量
names(data) <- c("work1", "work2", "ee1", "ee2", "ee3", "dpl1", "dpl2", "pa1", "pa2", "pa3", "Gender")
data$Gender <- factor(data$Gender, levels = c(1, 2), labels = c("male", "female"))
table(data$Gender)  # 查看性别分布

# 描述数据
summary(data)

结构方程模型

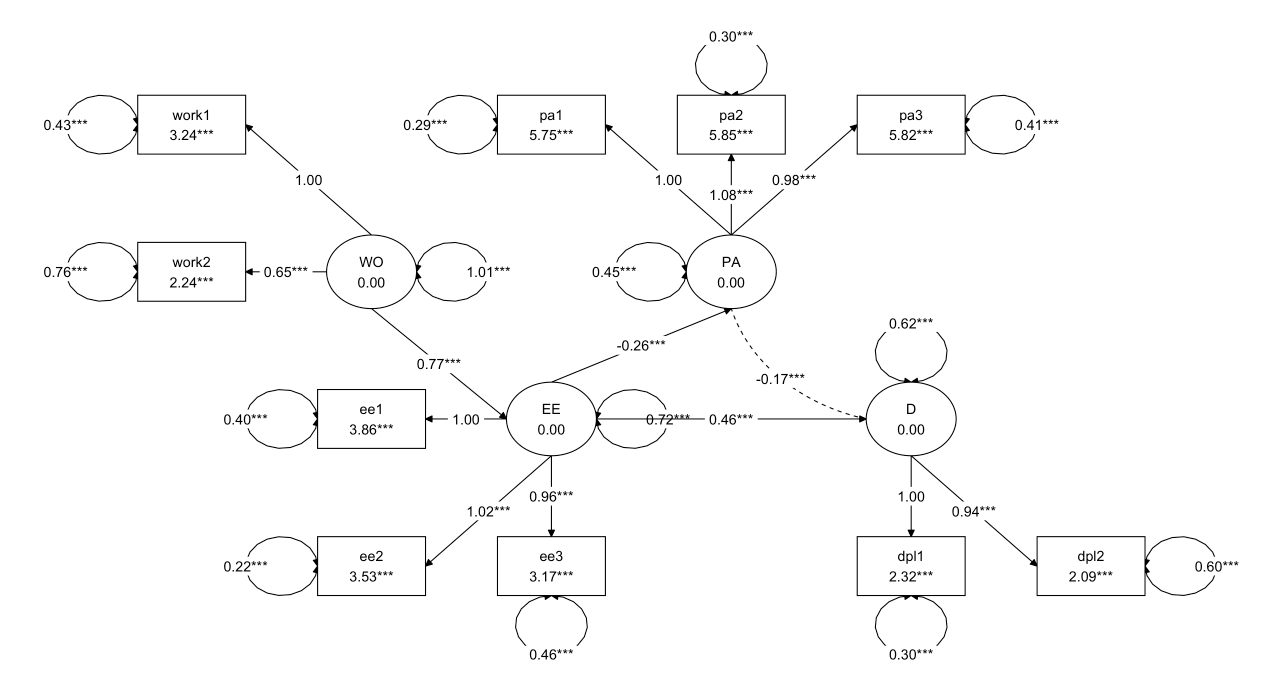
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
# 定义模型
model <- '
  # 测量模型
  EE =~ ee1 + ee2 + ee3       # EE 由 ee1, ee2, ee3 测量
  D =~ dpl1 + dpl2            # D 由 dpl1, dpl2 测量
  PA =~ pa1 + pa2 + pa3       # PA 由 pa1, pa2, pa3 测量
  WO =~ work1 + work2         # WO 由 work1, work2 测量

  # 结构模型
  EE ~ WO                     # EE 被 WO 预测
  D ~ EE                      # D 被 EE 预测
  PA ~ EE                     # PA 被 EE 预测

  # 协方差
  PA ~~ D                     # PA 和 D 之间的协方差
  
  # 截距
  ee1 ~ 1
  ee2 ~ 1
  ee3 ~ 1
  dpl1 ~ 1
  dpl2 ~ 1
  pa1 ~ 1
  pa2 ~ 1
  pa3 ~ 1
  work1 ~ 1
  work2 ~ 1
'

# 拟合模型
fit <- sem(model, data=data)
summary(fit, fit.measures=TRUE, standardized=TRUE, rsquare=TRUE)

# 可视化
layout_matrix <- matrix(NA, nrow = 4, ncol = 6, dimnames = list(NULL, NULL))
layout_matrix[1, 1] <- "work1"
layout_matrix[2, 1] <- "work2"
layout_matrix[2, 2] <- "WO"
layout_matrix[3, 3] <- "EE"
layout_matrix[3, 2] <- "ee1"
layout_matrix[4, 2] <- "ee2"
layout_matrix[4, 3] <- "ee3"
layout_matrix[2, 4] <- "PA"
layout_matrix[1, 3] <- "pa1"
layout_matrix[1, 4] <- "pa2"
layout_matrix[1, 5] <- "pa3"
layout_matrix[4, 5] <- "dpl1"
layout_matrix[4, 6] <- "dpl2"
layout_matrix[3, 5] <- "D"
graph_sem(fit, layout = layout_matrix, text_size = 5)

结构方程模型

模型拟合结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
Model Test User Model:
                                                      
  Test statistic                               301.492
  Degrees of freedom                                31
  P-value (Chi-square)                           0.000

Model Test Baseline Model:

  Test statistic                              7493.700
  Degrees of freedom                                45
  P-value                                        0.000

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.964
  Tucker-Lewis Index (TLI)                       0.947

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)             -18293.991
  Loglikelihood unrestricted model (H1)     -18143.245
                                                      
  Akaike (AIC)                               36655.982
  Bayesian (BIC)                             36835.006
  Sample-size adjusted Bayesian (SABIC)      36727.000

Root Mean Square Error of Approximation:

  RMSEA                                          0.078
  90 Percent confidence interval - lower         0.070
  90 Percent confidence interval - upper         0.086
  P-value H_0: RMSEA <= 0.050                    0.000
  P-value H_0: RMSEA >= 0.080                    0.360

Standardized Root Mean Square Residual:

  SRMR                                           0.040

可以看出，卡方值为301.492，自由度为31，CFI值为0.964，TLI值为0.947，RMSEA值为0.078，表明模型拟合较好。

模型估计结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  EE =~                                                                 
    ee1               1.000                               1.146    0.875
    ee2               1.017    0.021   48.938    0.000    1.166    0.927
    ee3               0.963    0.023   42.771    0.000    1.104    0.851
  D =~                                                                  
    dpl1              1.000                               0.947    0.865
    dpl2              0.941    0.044   21.591    0.000    0.891    0.754
  PA =~                                                                 
    pa1               1.000                               0.738    0.809
    pa2               1.076    0.036   29.617    0.000    0.794    0.825
    pa3               0.979    0.035   27.854    0.000    0.723    0.750
  WO =~                                                                 
    work1             1.000                               1.007    0.838
    work2             0.652    0.039   16.585    0.000    0.656    0.602

Regressions:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  EE ~                                                                  
    WO                0.766    0.046   16.490    0.000    0.673    0.673
  D ~                                                                   
    EE                0.462    0.024   19.325    0.000    0.559    0.559
  PA ~                                                                  
    EE               -0.262    0.019  -13.776    0.000   -0.408   -0.408

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
 .D ~~                                                                  
   .PA               -0.174    0.019   -8.950    0.000   -0.328   -0.328

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .ee1               3.855    0.035  111.347    0.000    3.855    2.944
   .ee2               3.530    0.033  106.201    0.000    3.530    2.808
   .ee3               3.165    0.034   92.281    0.000    3.165    2.440
   .dpl1              2.319    0.029   80.113    0.000    2.319    2.119
   .dpl2              2.086    0.031   66.763    0.000    2.086    1.765
   .pa1               5.748    0.024  238.172    0.000    5.748    6.298
   .pa2               5.850    0.025  229.759    0.000    5.850    6.076
   .pa3               5.815    0.025  228.188    0.000    5.815    6.034
   .work1             3.240    0.032  101.996    0.000    3.240    2.697
   .work2             2.243    0.029   77.885    0.000    2.243    2.060

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .ee1               0.400    0.021   19.017    0.000    0.400    0.234
   .ee2               0.222    0.017   13.108    0.000    0.222    0.140
   .ee3               0.463    0.022   20.743    0.000    0.463    0.275
   .dpl1              0.302    0.037    8.137    0.000    0.302    0.252
   .dpl2              0.603    0.039   15.621    0.000    0.603    0.432
   .pa1               0.288    0.017   16.743    0.000    0.288    0.346
   .pa2               0.296    0.019   15.573    0.000    0.296    0.320
   .pa3               0.406    0.020   20.150    0.000    0.406    0.438
   .work1             0.429    0.054    7.876    0.000    0.429    0.297
   .work2             0.756    0.036   21.071    0.000    0.756    0.637
   .EE                0.719    0.048   15.109    0.000    0.547    0.547
   .D                 0.616    0.044   14.058    0.000    0.687    0.687
   .PA                0.454    0.028   16.485    0.000    0.834    0.834
    WO                1.014    0.073   13.851    0.000    1.000    1.000

R-Square:
                   Estimate
    ee1               0.766
    ee2               0.860
    ee3               0.725
    dpl1              0.748
    dpl2              0.568
    pa1               0.654
    pa2               0.680
    pa3               0.562
    work1             0.703
    work2             0.363
    EE                0.453
    D                 0.313
    PA                0.166

结构方程模型多组比较

不同性别分别拟合模型

1
2
3
4
5
6
7
8
9
10
11
12
# 不同性别分别拟合模型
# 分别提取男性和女性的数据
data_male <- subset(data, Gender == "male")
data_female <- subset(data, Gender == "female")

# 对男性数据拟合模型
fit_male <- cfa(model, data = data_male)
summary(fit_male, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE)

# 对女性数据拟合模型
fit_female <- cfa(model, data = data_female)
summary(fit_female, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
> summary(fit_male, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE)

Model Test User Model:
                                                      
  Test statistic                               201.953
  Degrees of freedom                                31
  P-value (Chi-square)                           0.000

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.954
  Tucker-Lewis Index (TLI)                       0.933

Root Mean Square Error of Approximation:

  RMSEA                                          0.088
  90 Percent confidence interval - lower         0.077
  90 Percent confidence interval - upper         0.100
  P-value H_0: RMSEA <= 0.050                    0.000
  P-value H_0: RMSEA >= 0.080                    0.878

> summary(fit_female, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE)

Model Test User Model:
                                                      
  Test statistic                               157.743
  Degrees of freedom                                31
  P-value (Chi-square)                           0.000

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.967
  Tucker-Lewis Index (TLI)                       0.951

Root Mean Square Error of Approximation:

  RMSEA                                          0.076
  90 Percent confidence interval - lower         0.064
  90 Percent confidence interval - upper         0.087
  P-value H_0: RMSEA <= 0.050                    0.000
  P-value H_0: RMSEA >= 0.080                    0.276

结构模式相同模型(基线模型)

1
2
3
# 拟合基线模型（不包含等价约束）
fit_baseline <- sem(model, data = data, group = "Gender")
summary(fit_baseline, fit.measures=TRUE, standardized=TRUE, rsquare=TRUE)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
> summary(fit_baseline, fit.measures=TRUE, standardized=TRUE, rsquare=TRUE)

Model Test User Model:
                                                      
  Test statistic                               359.696
  Degrees of freedom                                62
  P-value (Chi-square)                           0.000
  Test statistic for each group:
    female                                     157.743
    male                                       201.953

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.960
  Tucker-Lewis Index (TLI)                       0.942

Root Mean Square Error of Approximation:

  RMSEA                                          0.082
  90 Percent confidence interval - lower         0.074
  90 Percent confidence interval - upper         0.090
  P-value H_0: RMSEA <= 0.050                    0.000
  P-value H_0: RMSEA >= 0.080                    0.662

可以看出RMSEA值为0.082，CFI的值为0.960，TLI的值为0.942，卡方值为359.696，自由度为62，表明模型拟合较好。该模型作为基线模型，用于检验其他等价性条件是否满足。

测量模型：因素载荷等价模型(弱等价性)

1
2
3
4
# 测量模型部分 - 因素载荷等价
fit_metric <- update(fit_baseline, group.equal = "loadings")
summary(fit_metric, fit.measures=TRUE, standardized=TRUE, rsquare=TRUE)
anova(fit_baseline, fit_metric)
1
2
3
4
5
6
7
> anova(fit_baseline, fit_metric)

Chi-Squared Difference Test

             Df   AIC   BIC  Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
fit_baseline 62 36683 37041 359.70                                    
fit_metric   68 36675 37002 364.27     4.5749     0       6     0.5994

弱等价性模型嵌套于基线模型，可以使用嵌套模型的比较方法。

可以看出两个模型的卡方值的差值Chisq diff为4.5749，自由度的差值Df diff为6，表明两个模型的卡方差异不显著。可以接受弱等价模型，即认为不同性别之间满足因素载荷等价条件。

测量模型：误差协方差矩阵等价模型

1
2
3
4
# 测量模型部分 - 误差协方差矩阵等价
fit_residuals <- update(fit_metric, group.equal = c("loadings", "residuals"))
summary(fit_residuals, fit.measures=TRUE, standardized=TRUE, rsquare=TRUE)
anova(fit_baseline, fit_metric, fit_residuals)
1
2
3
4
5
6
7
8
> anova(fit_baseline, fit_metric, fit_residuals)

Chi-Squared Difference Test

              Df   AIC   BIC  Chisq Chisq diff    RMSEA Df diff Pr(>Chisq)
fit_baseline  62 36683 37041 359.70                                       
fit_metric    68 36675 37002 364.27     4.5749 0.000000       6     0.5994
fit_residuals 78 36670 36944 379.52    15.2466 0.027089      10     0.1233

可以看出两个模型的卡方值的差值Chisq diff为15.2466，自由度的差值Df diff为10，表明两个模型的卡方差异不显著。可以接受误差方差等价模型，即认为不同性别之间满足误差方差等价条件。

测量模型：截距等价模型

1
2
3
fit_scalar <- update(fit_residuals, group.equal = c("loadings", "residuals", "intercepts"))
summary(fit_scalar, fit.measures=TRUE, standardized=TRUE, rsquare=TRUE)
anova(fit_baseline, fit_metric, fit_residuals, fit_scalar)
1
2
3
4
5
6
7
8
9
> anova(fit_baseline, fit_metric, fit_residuals, fit_scalar)

Chi-Squared Difference Test

              Df   AIC   BIC  Chisq Chisq diff    RMSEA Df diff Pr(>Chisq)
fit_baseline  62 36683 37041 359.70                                       
fit_metric    68 36675 37002 364.27     4.5749 0.000000       6     0.5994
fit_residuals 78 36670 36944 379.52    15.2466 0.027089      10     0.1233
fit_scalar    84 36663 36905 384.07     4.5511 0.000000       6     0.6025

可以看出两个模型的卡方值的差值Chisq diff为4.5511，自由度的差值Df diff为6，表明两个模型的卡方差异不显著。可以接受强等价模型，即认为不同性别之间满足截距等价条件。

结构模型：潜变量路径系数等价模型

1
2
3
4
# 潜变量相关或回归系数等价性检验
fit_structural <- update(fit_scalar, group.equal = c("loadings", "residuals", "intercepts", "regressions"))
summary(fit_structural, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE)
anova(fit_baseline, fit_metric, fit_residuals, fit_scalar, fit_structural)
1
2
3
4
5
6
7
8
9
10
> anova(fit_baseline, fit_metric, fit_residuals, fit_scalar, fit_structural)

Chi-Squared Difference Test

               Df   AIC   BIC  Chisq Chisq diff    RMSEA Df diff Pr(>Chisq)
fit_baseline   62 36683 37041 359.70                                       
fit_metric     68 36675 37002 364.27     4.5749 0.000000       6     0.5994
fit_residuals  78 36670 36944 379.52    15.2466 0.027089      10     0.1233
fit_scalar     84 36663 36905 384.07     4.5511 0.000000       6     0.6025
fit_structural 87 36662 36889 389.60     5.5357 0.034382       3     0.1365

可以看出两个模型的卡方值的差值Chisq diff为5.5357，自由度的差值Df diff为4，表明两个模型的卡方差异不显著。可以接受潜变量路径系数等价模型，即认为不同性别之间满足路径系数等价条件。

结构模型：潜变量协方差矩阵等价模型

1
2
3
4
# 结构模型部分 - 潜变量协方差矩阵等价
fit_covariance <- update(fit_structural, group.equal = c("loadings", "residuals", "intercepts", "regressions", "lv.covariances"))
summary(fit_covariance, fit.measures=TRUE, standardized=TRUE, rsquare=TRUE)
anova(fit_baseline, fit_metric, fit_residuals, fit_scalar, fit_structural, fit_covariance)
1
2
3
4
5
6
7
8
9
10
11
> anova(fit_baseline, fit_metric, fit_residuals, fit_scalar, fit_structural, fit_covariance)

Chi-Squared Difference Test

               Df   AIC   BIC  Chisq Chisq diff    RMSEA Df diff Pr(>Chisq)
fit_baseline   62 36683 37041 359.70                                       
fit_metric     68 36675 37002 364.27     4.5749 0.000000       6     0.5994
fit_residuals  78 36670 36944 379.52    15.2466 0.027089      10     0.1233
fit_scalar     84 36663 36905 384.07     4.5511 0.000000       6     0.6025
fit_structural 87 36662 36889 389.60     5.5357 0.034382       3     0.1365
fit_covariance 88 36662 36883 391.08     1.4783 0.025865       1     0.2240

可以看出两个模型的卡方值的差值Chisq diff为1.4783，自由度的差值Df diff为1，表明两个模型的卡方差异不显著。可以接受潜变量协方差等价模型，即认为不同性别之间满足潜变量协方差等价条件。

结构模型：潜变量方差等价模型

1
2
3
4
# 结构模型部分 - 潜变量方差等价
fit_variances <- update(fit_covariance, group.equal = c("loadings", "residuals", "intercepts", "regressions", "lv.covariances", "lv.variances"))
summary(fit_variances, fit.measures=TRUE, standardized=TRUE, rsquare=TRUE)
anova(fit_baseline, fit_metric, fit_residuals, fit_scalar, fit_covariance, fit_variances)
1
2
3
4
5
6
7
8
9
10
11
12
> anova(fit_baseline, fit_metric, fit_residuals, fit_scalar, fit_structural, fit_covariance, fit_variances)

Chi-Squared Difference Test

               Df   AIC   BIC  Chisq Chisq diff    RMSEA Df diff Pr(>Chisq)
fit_baseline   62 36683 37041 359.70                                       
fit_metric     68 36675 37002 364.27     4.5749 0.000000       6     0.5994
fit_residuals  78 36670 36944 379.52    15.2466 0.027089      10     0.1233
fit_scalar     84 36663 36905 384.07     4.5511 0.000000       6     0.6025
fit_structural 87 36662 36889 389.60     5.5357 0.034382       3     0.1365
fit_covariance 88 36662 36883 391.08     1.4783 0.025865       1     0.2240
fit_variances  92 36660 36860 397.44     6.3575 0.028710       4     0.1740

可以看出两个模型的卡方值的差值Chisq diff为6.3575，自由度的差值Df diff为4，表明两个模型的卡方差异不显著。可以接受潜变量方差等价模型，即认为不同性别之间满足潜变量方差等价条件。

结构模型：潜在因素均值等价模型

1
2
3
4
# 结构模型部分 - 潜在因素均值等价
fit_means <- update(fit_variances, group.equal = c("loadings", "residuals", "intercepts", "regressions", "lv.covariances", "lv.variances", "means"))
summary(fit_means, fit.measures=TRUE, standardized=TRUE, rsquare=TRUE)
anova(fit_baseline, fit_metric, fit_residuals, fit_scalar, fit_covariance, fit_means)
1
2
3
4
5
6
7
8
9
10
11
12
13
> anova(fit_baseline, fit_metric, fit_residuals, fit_scalar, fit_structural, fit_covariance, fit_variances, fit_means)

Chi-Squared Difference Test

               Df   AIC   BIC  Chisq Chisq diff    RMSEA Df diff Pr(>Chisq)
fit_baseline   62 36683 37041 359.70                                       
fit_metric     68 36675 37002 364.27     4.5749 0.000000       6     0.5994
fit_residuals  78 36670 36944 379.52    15.2466 0.027089      10     0.1233
fit_scalar     84 36663 36905 384.07     4.5511 0.000000       6     0.6025
fit_structural 87 36662 36889 389.60     5.5357 0.034382       3     0.1365
fit_covariance 88 36662 36883 391.08     1.4783 0.025865       1     0.2240
fit_variances  92 36660 36860 397.44     6.3575 0.028710       4     0.1740
fit_means      96 36656 36835 401.14     3.6989 0.000000       4     0.4483

可以看出两个模型的卡方值的差值Chisq diff为3.6989，自由度的差值Df diff为4，表明两个模型的卡方差异不显著。可以接受潜变量均值等价模型，即认为不同性别之间满足潜变量均值等价条件。

中介分析

导入包与数据

1
2
3
4
5
6
7
8
9
10
11
12
# 导入包
library(lavaan)
library(tidySEM)
library(blavaan)

# 导入数据
setwd("/Users/nanxu/研究生课程作业/心理统计/课件数据/11第十一章 中介分析/")
data <- read.table("./11_4 med.dat", header = FALSE, sep = "", na.strings = "NA")

# 查看数据
names(data)
dim(data)

数据介绍

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 数据名称
# ID -- V1
# nrel1 -- V2
# nrel2 -- V3
# nrel3 -- V4
# prel1 -- V5
# prel2 -- V6
# prel3 -- V7
# pem1 -- V8
# pem2 -- V9
# pem3 -- V10
# nem1 -- V11
# nem2 -- V12
# nem3 -- V13
# sat1 -- V14
# sat2 -- V15
# sat3 -- V16
# nrel_m -- V17
# prel_m -- V18
# pem_m -- V19
# mem_m -- V20
# sat_m -- V21

# 变量重命名
names(data) <- c("ID", "nrel1", "nrel2", "nrel3", "prel1", "prel2", "prel3", 
                 "pem1", "pem2", "pem3", "nem1", "nem2", "nem3", "sat1", "sat2", 
                 "sat3", "nrel_m", "prel_m", "pem_m", "nem_m", "sat_m")

# 描述数据
summary(data)

中介分析模型

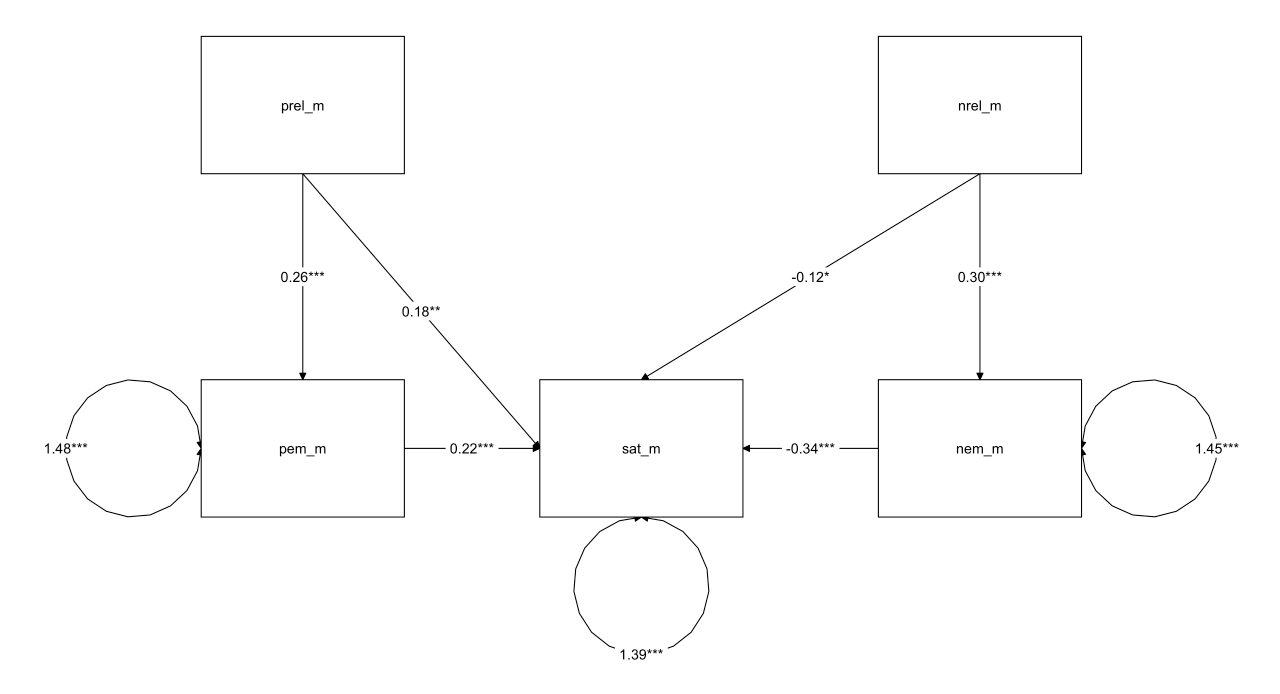
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 定义中介分析模型
med_model <- '
  # 直接效应
  sat_m ~ a1*pem_m + a2*nem_m + a3*prel_m + a4*nrel_m
  pem_m ~ b*prel_m
  nem_m ~ c*nrel_m

  # 计算间接效应（使用正确的参数定义方式）
  # 间接效应: sat_m 对 pem_m 通过 prel_m
  ind_pem_sat := b * a1
  # 间接效应: sat_m 对 nem_m 通过 nrel_m
  ind_nem_sat := c * a2
'

fit <- sem(med_model, data=data)

# 可视化
layout_matrix <- matrix(NA, nrow = 2, ncol = 3, dimnames = list(NULL, NULL))
layout_matrix[1, 1] <- "prel_m"
layout_matrix[1, 3] <- "nrel_m"
layout_matrix[2, 1] <- "pem_m"
layout_matrix[2, 2] <- "sat_m"
layout_matrix[2, 3] <- "nem_m"
graph_sem(fit, layout = layout_matrix, text_size = 5)

中介分析模型

Sobel检验

1
2
fit1 <- sem(med_model, data=data)
summary(fit1, fit.measures=TRUE, standardized=TRUE, rsquare=TRUE)

模型拟合结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
Model Test User Model:
                                                      
  Test statistic                                 2.804
  Degrees of freedom                                 3
  P-value (Chi-square)                           0.423

Model Test Baseline Model:

  Test statistic                               109.942
  Degrees of freedom                                 9
  P-value                                        0.000

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    1.000
  Tucker-Lewis Index (TLI)                       1.006

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -1249.213
  Loglikelihood unrestricted model (H1)      -1247.811
                                                      
  Akaike (AIC)                                2516.426
  Bayesian (BIC)                              2548.472
  Sample-size adjusted Bayesian (SABIC)       2519.938

Root Mean Square Error of Approximation:

  RMSEA                                          0.000
  90 Percent confidence interval - lower         0.000
  90 Percent confidence interval - upper         0.102
  P-value H_0: RMSEA <= 0.050                    0.664
  P-value H_0: RMSEA >= 0.080                    0.135

Standardized Root Mean Square Residual:

  SRMR                                           0.025

可以看出，卡方值为2.804，自由度为3，CFI值为1.000，TLI值为1.006，RMSEA值为0.000，表明模型拟合较好。

参数估计结果与标准化参数估计结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Regressions:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  sat_m ~                                                               
    pem_m     (a1)    0.219    0.060    3.654    0.000    0.219    0.206
    nem_m     (a2)   -0.335    0.061   -5.543    0.000   -0.335   -0.317
    prel_m    (a3)    0.184    0.062    2.972    0.003    0.184    0.168
    nrel_m    (a4)   -0.121    0.062   -1.966    0.049   -0.121   -0.112
  pem_m ~                                                               
    prel_m     (b)    0.256    0.062    4.140    0.000    0.256    0.249
  nem_m ~                                                               
    nrel_m     (c)    0.297    0.061    4.907    0.000    0.297    0.291

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .sat_m             1.385    0.121   11.402    0.000    1.385    0.778
   .pem_m             1.484    0.130   11.402    0.000    1.484    0.938
   .nem_m             1.455    0.128   11.402    0.000    1.455    0.915

R-Square:
                   Estimate
    sat_m             0.222
    pem_m             0.062
    nem_m             0.085

中介效应检验结果

1
2
3
4
Defined Parameters:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    ind_pem_sat       0.056    0.020    2.739    0.006    0.056    0.051
    ind_nem_sat      -0.100    0.027   -3.674    0.000   -0.100   -0.092

两个中介效应结果显著。

Bootstrap检验

1
2
3
4
5
6
7
8
9
10
# Bootstrap检验
fit2 <- sem(med_model, data=data, se="bootstrap", bootstrap=1000)

# 查看模型摘要，包括偏差修正的 bootstrap 置信区间
summary(fit2, fit.measures=TRUE, standardized=TRUE, rsquare=TRUE)

# 查看参数估计，包括不同置信水平的偏差修正的 bootstrap 置信区间
parameterEstimates(fit2, level=0.90, boot.ci.type="bca")
parameterEstimates(fit2, level=0.95, boot.ci.type="bca")
parameterEstimates(fit2, level=0.99, boot.ci.type="bca")

结果呈现了估计值est、90%置信区间、95%置信区间、99%置信区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
> parameterEstimates(fit2, level=0.90, boot.ci.type="bca")
           lhs op    rhs       label    est    se      z pvalue ci.lower ci.upper
13 ind_pem_sat :=   b*a1 ind_pem_sat  0.056 0.020  2.803  0.005    0.029    0.096
14 ind_nem_sat :=   c*a2 ind_nem_sat -0.100 0.027 -3.733  0.000   -0.148   -0.061

> parameterEstimates(fit2, level=0.95, boot.ci.type="bca")
           lhs op    rhs       label    est    se      z pvalue ci.lower ci.upper
13 ind_pem_sat :=   b*a1 ind_pem_sat  0.056 0.020  2.803  0.005    0.024    0.103
14 ind_nem_sat :=   c*a2 ind_nem_sat -0.100 0.027 -3.733  0.000   -0.158   -0.054

> parameterEstimates(fit2, level=0.99, boot.ci.type="bca")
           lhs op    rhs       label    est    se      z pvalue ci.lower ci.upper
13 ind_pem_sat :=   b*a1 ind_pem_sat  0.056 0.020  2.803  0.005    0.016    0.118
14 ind_nem_sat :=   c*a2 ind_nem_sat -0.100 0.027 -3.733  0.000   -0.183   -0.044

两个中介效应的置信区间均不包括0，说明两个中介效应均在0.10、0.05、0.01水平上显著

MCMC方法

1
2
3
4
5
6
7
8
9
10
fit3 <- bsem(med_model, data = data,
             n.chains = 2,         # 使用4个MCMC链
             burnin = 1000,         # 烧入期迭代次数
             sample = 30000,        # 采样次数
             adapt = 1000,         # 自适应迭代次数
             target = "stan",      # 使用 Stan 为MCMC后端
             seed = 12345,         # 设置随机种子以确保结果的可复现性
             save.lvs = FALSE)     # 是否保存潜变量分数

summary(fit3)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Regressions:
                   Estimate  Post.SD pi.lower pi.upper     Rhat    Prior       
  sat_m ~                                                                      
    pem_m     (a1)    0.219    0.061    0.101    0.337    1.000    normal(0,10)
    nem_m     (a2)   -0.335    0.061   -0.455   -0.215    1.000    normal(0,10)
    prel_m    (a3)    0.184    0.063    0.060    0.307    1.000    normal(0,10)
    nrel_m    (a4)   -0.121    0.063   -0.245    0.002    1.000    normal(0,10)
  pem_m ~                                                                      
    prel_m     (b)    0.257    0.062    0.135    0.378    1.000    normal(0,10)
  nem_m ~                                                                      
    nrel_m     (c)    0.297    0.061    0.177    0.415    1.000    normal(0,10)

Variances:
                   Estimate  Post.SD pi.lower pi.upper     Rhat    Prior       
   .sat_m             1.420    0.126    1.194    1.689    1.000 gamma(1,.5)[sd]
   .pem_m             1.503    0.134    1.264    1.791    1.000 gamma(1,.5)[sd]
   .nem_m             1.474    0.132    1.238    1.754    1.000 gamma(1,.5)[sd]

Defined Parameters:
                   Estimate  Post.SD pi.lower pi.upper     Rhat    Prior       
    ind_pem_sat       0.056    0.021    0.015    0.097                         
    ind_nem_sat      -0.099    0.028   -0.154   -0.045

可以看出ind_pem_sat中介效应的95%置信区间估计为[0.015, 0.097]，ind_nem_sat中介效应的95%置信区间估计为[-0.154, -0.045]

潜变量中介分析

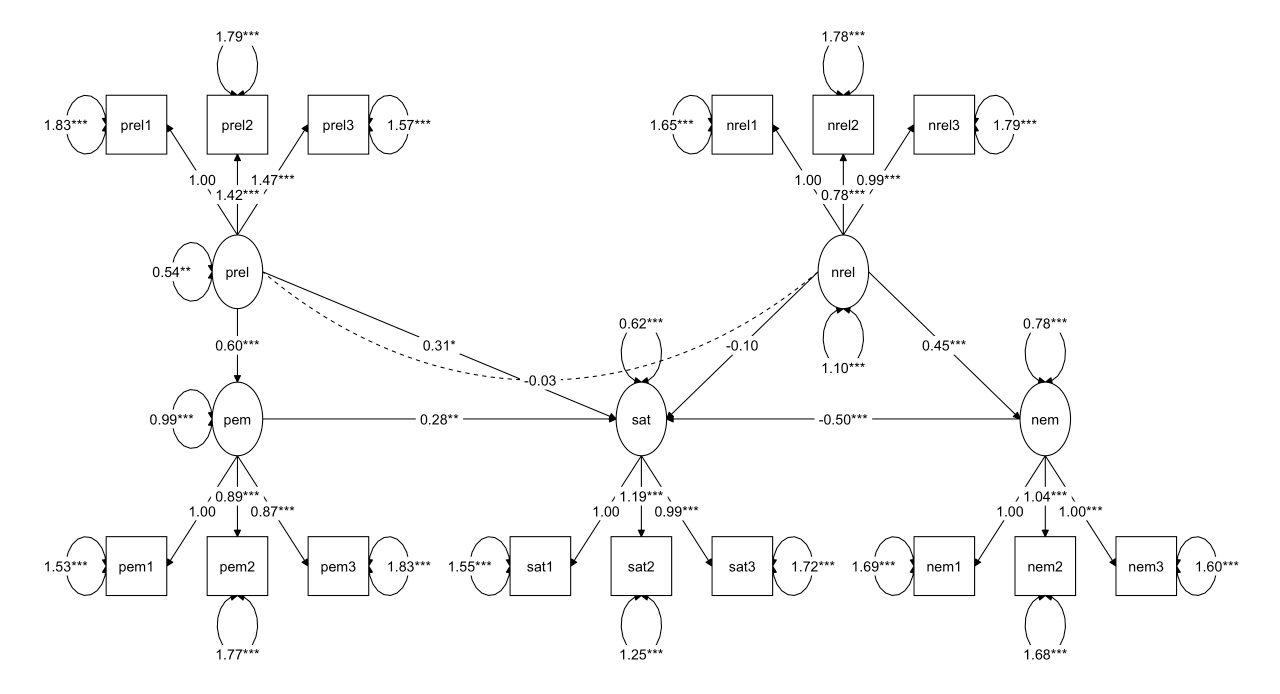
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
# 潜变量中介模型
med_latent_model <- '
  # 测量模型
  nrel =~ nrel1 + nrel2 + nrel3
  prel =~ prel1 + prel2 + prel3
  nem =~ nem1 + nem2 + nem3
  pem =~ pem1 + pem2 + pem3
  sat =~ sat1 + sat2 + sat3

  # 结构模型
  sat ~ a1*pem + a2*nem + a3*prel + a4*nrel
  pem ~ b*prel
  nem ~ c*nrel

  # 间接效应
  # sat 对 pem 通过 prel
  sat_prel_prel := b * a1
  # sat 对 nem 通过 nrel
  sat_nrel_nrel := c * a2
'

# 拟合模型
fit3 <- sem(med_latent_model, data=data)
summary(fit3, fit.measures=TRUE, standardized=TRUE, rsquare=TRUE)

# 可视化
layout_matrix <- matrix(NA, nrow = 4, ncol = 11, dimnames = list(NULL, NULL))
layout_matrix[1, 1] <- "prel1"
layout_matrix[1, 2] <- "prel2"
layout_matrix[1, 3] <- "prel3"
layout_matrix[2, 2] <- "prel"
layout_matrix[1, 7] <- "nrel1"
layout_matrix[1, 8] <- "nrel2"
layout_matrix[1, 9] <- "nrel3"
layout_matrix[2, 8] <- "nrel"
layout_matrix[4, 1] <- "pem1"
layout_matrix[4, 2] <- "pem2"
layout_matrix[4, 3] <- "pem3"
layout_matrix[3, 2] <- "pem"
layout_matrix[4, 5] <- "sat1"
layout_matrix[4, 6] <- "sat2"
layout_matrix[4, 7] <- "sat3"
layout_matrix[3, 6] <- "sat"
layout_matrix[4, 9] <- "nem1"
layout_matrix[4, 10] <- "nem2"
layout_matrix[4, 11] <- "nem3"
layout_matrix[3, 10] <- "nem"
graph_sem(fit3, layout = layout_matrix, text_size = 5)

潜变量中介分析

模型拟合结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
Model Test User Model:
                                                      
  Test statistic                                80.049
  Degrees of freedom                                83
  P-value (Chi-square)                           0.571

Model Test Baseline Model:

  Test statistic                               714.854
  Degrees of freedom                               105
  P-value                                        0.000

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    1.000
  Tucker-Lewis Index (TLI)                       1.006

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -7162.602
  Loglikelihood unrestricted model (H1)      -7122.577
                                                      
  Akaike (AIC)                               14399.204
  Bayesian (BIC)                             14530.950
  Sample-size adjusted Bayesian (SABIC)      14413.645

Root Mean Square Error of Approximation:

  RMSEA                                          0.000
  90 Percent confidence interval - lower         0.000
  90 Percent confidence interval - upper         0.032
  P-value H_0: RMSEA <= 0.050                    1.000
  P-value H_0: RMSEA >= 0.080                    0.000

Standardized Root Mean Square Residual:

  SRMR                                           0.043

参数估计结果与标准化参数估计结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  nrel =~                                                               
    nrel1             1.000                               1.051    0.633
    nrel2             0.782    0.147    5.334    0.000    0.822    0.524
    nrel3             0.989    0.179    5.515    0.000    1.039    0.614
  prel =~                                                               
    prel1             1.000                               0.736    0.478
    prel2             1.422    0.282    5.047    0.000    1.047    0.616
    prel3             1.471    0.293    5.022    0.000    1.083    0.654
  nem =~                                                                
    nem1              1.000                               1.004    0.612
    nem2              1.045    0.163    6.422    0.000    1.048    0.628
    nem3              1.000    0.156    6.399    0.000    1.003    0.621
  pem =~                                                                
    pem1              1.000                               1.090    0.661
    pem2              0.894    0.153    5.852    0.000    0.975    0.591
    pem3              0.869    0.150    5.809    0.000    0.948    0.573
  sat =~                                                                
    sat1              1.000                               1.065    0.650
    sat2              1.189    0.148    8.059    0.000    1.266    0.750
    sat3              0.994    0.132    7.557    0.000    1.058    0.627

Regressions:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  sat ~                                                                 
    pem       (a1)    0.278    0.099    2.806    0.005    0.285    0.285
    nem       (a2)   -0.498    0.126   -3.963    0.000   -0.469   -0.469
    prel      (a3)    0.310    0.147    2.108    0.035    0.215    0.215
    nrel      (a4)   -0.096    0.105   -0.912    0.362   -0.095   -0.095
  pem ~                                                                 
    prel       (b)    0.599    0.174    3.440    0.001    0.404    0.404
  nem ~                                                                 
    nrel       (c)    0.449    0.112    4.017    0.000    0.470    0.470

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  nrel ~~                                                               
    prel             -0.034    0.075   -0.457    0.648   -0.044   -0.044

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .nrel1             1.653    0.237    6.965    0.000    1.653    0.599
   .nrel2             1.779    0.199    8.939    0.000    1.779    0.725
   .nrel3             1.787    0.243    7.366    0.000    1.787    0.623
   .prel1             1.828    0.193    9.469    0.000    1.828    0.771
   .prel2             1.793    0.251    7.151    0.000    1.793    0.621
   .prel3             1.570    0.248    6.326    0.000    1.570    0.572
   .nem1              1.686    0.204    8.265    0.000    1.686    0.626
   .nem2              1.685    0.211    7.971    0.000    1.685    0.605
   .nem3              1.602    0.198    8.099    0.000    1.602    0.614
   .pem1              1.532    0.228    6.709    0.000    1.532    0.563
   .pem2              1.773    0.218    8.130    0.000    1.773    0.651
   .pem3              1.835    0.218    8.434    0.000    1.835    0.671
   .sat1              1.549    0.181    8.542    0.000    1.549    0.577
   .sat2              1.247    0.193    6.456    0.000    1.247    0.437
   .sat3              1.724    0.194    8.888    0.000    1.724    0.606
    nrel              1.105    0.270    4.094    0.000    1.000    1.000
    prel              0.542    0.171    3.179    0.001    1.000    1.000
   .nem               0.784    0.195    4.014    0.000    0.779    0.779
   .pem               0.994    0.241    4.124    0.000    0.837    0.837
   .sat               0.616    0.149    4.141    0.000    0.543    0.543

R-Square:
                   Estimate
    nrel1             0.401
    nrel2             0.275
    nrel3             0.377
    prel1             0.229
    prel2             0.379
    prel3             0.428
    nem1              0.374
    nem2              0.395
    nem3              0.386
    pem1              0.437
    pem2              0.349
    pem3              0.329
    sat1              0.423
    sat2              0.563
    sat3              0.394
    nem               0.221
    pem               0.163
    sat               0.457

Sobel检验

1
2
3
4
Defined Parameters:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    sat_prel_sat      0.167    0.071    2.348    0.019    0.115    0.115
    sat_nrel_sat     -0.224    0.073   -3.054    0.002   -0.221   -0.221

结果显示，两个中介效应均显著

调节效应

两个连续变量的调节作用

自变量XX、调节变量MM与因变量YY均为观测变量

导入包与数据

1
2
3
4
5
6
7
8
9
10
11
12
# 导入包
library(haven)
library(lavaan)
library(dplyr)

# 导入数据
setwd("/Users/nanxu/研究生课程作业/心理统计/课件数据/12第十二章 调节效应/")
data <- read_sav("./12_1 mod_1.sav")

# 查看数据
names(data)
dim(data)

数据介绍与预处理

1
2
3
4
5
6
# 描述数据
summary(data)

# 计算相关系数矩阵
cor_matrix <- cor(data[, 1:3], use="complete.obs")
cor.plot(cor_matrix)

相关矩阵

1
2
3
4
5
6
7
8
9
10
11
12
# 中心化变量
data$CSC <- scale(data$SC, scale = FALSE)[, 1]
data$CSS <- scale(data$SS, scale = FALSE)[, 1]

# 标准化变量
data$ZSC <- scale(data$SC)[, 1]
data$ZSS <- scale(data$SS)[, 1]
data$ZDEP <- scale(data$DEP)[, 1]

# 创建交互项
data$CSSCSC <- data$CSC * data$CSS
data$ZSSZSC <- data$ZSC * data$ZSS

非标准化解

将自变量XX与调节变量MM做中心化处理

1
2
3
4
5
6
7
8
9
10
# 非标准化
# 第一层回归：包括CSS和CSC
fit1 <- lm(DEP ~ CSS + CSC, data = data)
summary(fit1)  # 输出模型结果

# 第二层回归：添加交互项CSSCSC
fit2 <- lm(DEP ~ CSS + CSC + CSSCSC, data = data)
summary(fit2)  # 输出模型结果

anova(fit1, fit2)

回归系数估计结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
> summary(fit1)  # 输出模型结果

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.55711    0.05698  44.874  < 2e-16 ***
CSS          0.30851    0.09203   3.352 0.000937 ***
CSC         -0.23512    0.11750  -2.001 0.046571 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.8698 on 230 degrees of freedom
Multiple R-squared:  0.06211,	Adjusted R-squared:  0.05395 
F-statistic: 7.615 on 2 and 230 DF,  p-value: 0.0006274

> summary(fit2)  # 输出模型结果

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.55764    0.05652  45.253  < 2e-16 ***
CSS          0.30119    0.09134   3.298  0.00113 ** 
CSC         -0.23638    0.11654  -2.028  0.04369 *  
CSSCSC      -2.29489    1.04575  -2.194  0.02920 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.8627 on 229 degrees of freedom
Multiple R-squared:  0.08143,	Adjusted R-squared:  0.06939 
F-statistic: 6.767 on 3 and 229 DF,  p-value: 0.0002163

模型比较结果

1
2
3
4
5
> anova(fit1, fit2)

  Res.Df    RSS Df Sum of Sq      F Pr(>F)  
1    230 174.02                             
2    229 170.44  1    3.5842 4.8158 0.0292 *

可以看出，社会支持与工作压力的交互作用CSSCSC显著

绘制工作压力对抑郁的影像图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 绘制影响图
points_data <- data.frame(
  CSC = rep(c(-sd(data$CSC), 0, sd(data$CSC)), each = 2),
  CSS = rep(c(-1, 1), times = 3) * sd(data$CSS),
  Group = rep(c("Low SS", "Mean SS", "High SS"), each = 2)
)
points_data$CSSCSC <- points_data$CSS * points_data$CSC
points_data$Predicted_DEP <- predict(fit2_1, newdata = points_data)

plot(points_data$CSS, points_data$Predicted_DEP, type = 'n',
     xlab = "Social Support (Centered)", ylab = "Predicted Depression",
     main = "Effect of Social Support and Work Pressure on Depression")
colors <- c("red", "blue", "green")
for (i in unique(points_data$Group)) {
  subset_data <- points_data[points_data$Group == i,]
  points(subset_data$CSS, subset_data$Predicted_DEP, col = colors[which(unique(points_data$Group) == i)], pch = 19)
  lines(subset_data$CSS, subset_data$Predicted_DEP, col = colors[which(unique(points_data$Group) == i)], lwd = 2)
}
legend("topleft", legend = c("-1 SD", "Mean", "+1 SD"), col = colors, lwd = 2, title = "CSC Levels")

在不同的社会支持水平上，工作压力对抑郁倾向的影响)

效应量

表示交互作用对因变量变异方差解释与没有解释的变异的比值

f2=R包含交互2−R不包含交互21−R包含交互2f^2 = \frac{R^2 _{包含交互} - R^2 _{不包含交互}}{1 - R^2 _{包含交互}}

f2=0.02f^2 = 0.02表示小的效应，f2=0.15f^2 = 0.15表示中等的效应，f2=0.026f^2 = 0.026表示大的效应，

1
2
3
4
5
6
7
8
# 效应量
# 假设fit_basic和fit_full已经被拟合
R2_excluded <- summary(fit1)$r.squared  # 基础模型的R^2
R2_included <- summary(fit2)$r.squared   # 完整模型的R^2

# 计算f^2系数
> (R2_included - R2_excluded) / (1 - R2_included)
[1] 0.02102979

标准化解

自变量XX、调节变量MM与因变量YY做标准化处理

1
2
3
4
5
6
7
8
9
# 标准化
fit3 <- lm(ZDEP ~ ZSS + ZSC, data = data)
summary(fit3)  # 输出模型结果

# 第二层回归：添加交互项CSSCSC
fit4 <- lm(ZDEP ~ ZSS + ZSC + ZSSZSC, data = data)
summary(fit4)  # 输出模型结果

anova(fit3, fit4)

回归系数估计结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
> summary(fit3)  # 输出模型结果

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -3.933e-16  6.372e-02   0.000 1.000000    
ZSS          2.141e-01  6.386e-02   3.352 0.000937 ***
ZSC         -1.278e-01  6.386e-02  -2.001 0.046571 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.9726 on 230 degrees of freedom
Multiple R-squared:  0.06211,	Adjusted R-squared:  0.05395 
F-statistic: 7.615 on 2 and 230 DF,  p-value: 0.0006274

> summary(fit4)  # 输出模型结果

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept)  0.000597   0.063199   0.009  0.99247   
ZSS          0.208985   0.063377   3.298  0.00113 **
ZSC         -0.128460   0.063335  -2.028  0.04369 * 
ZSSZSC      -0.773876   0.352644  -2.194  0.02920 * 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.9647 on 229 degrees of freedom
Multiple R-squared:  0.08143,	Adjusted R-squared:  0.06939 
F-statistic: 6.767 on 3 and 229 DF,  p-value: 0.0002163

绘制工作压力对抑郁的影像图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 绘制影响图
points_data <- data.frame(
  ZSC = rep(c(-1, 0, 1), each = 2),
  ZSS = rep(c(-1, 1), times = 3),
  Group = rep(c("Low SS", "Mean SS", "High SS"), each = 2)
)
points_data$ZSSZSC <- points_data$ZSS * points_data$ZSC
points_data$Predicted_DEP <- predict(fit4, newdata = points_data)

plot(points_data$ZSS, points_data$Predicted_DEP, type = 'n',
     xlab = "Social Support (Centered)", ylab = "Predicted Depression",
     main = "Effect of Social Support and Work Pressure on Depression")
colors <- c("red", "blue", "green")
for (i in unique(points_data$Group)) {
  subset_data <- points_data[points_data$Group == i,]
  points(subset_data$ZSS, subset_data$Predicted_DEP, col = colors[which(unique(points_data$Group) == i)], pch = 19)
  lines(subset_data$ZSS, subset_data$Predicted_DEP, col = colors[which(unique(points_data$Group) == i)], lwd = 2)
}
legend("topleft", legend = c("-1 SD", "Mean", "+1 SD"), col = colors, lwd = 2, title = "CSC Levels")

在不同的社会支持水平上，工作压力对抑郁倾向的影响

简单斜率检验

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 简单斜率检验
# 创建交互项并为M低于均值一个标准差时的简单斜率添加变量
data <- data %>%
  mutate(
    ZSCBELOW = ZSC + 1,  # ZSC低于均值一个标准差
    ZSS_ZSCBELOW = ZSS * ZSCBELOW,  # 交互项
    ZSCABOVE = ZSC - 1,  # ZSC高于均值一个标准差
    ZSS_ZSCABOVE = ZSS * ZSCABOVE   # 交互项
  )

# 第一步回归：基本效应模型（没有交互项）
# fit3 <- lm(ZDEP ~ ZSS + ZSC, data = data)
summary(fit3)

# 第二步回归：测试M低于均值一个标准差时的简单斜率
fit_below <- lm(ZDEP ~ ZSS + ZSCBELOW + ZSS_ZSCBELOW, data = data)
summary(fit_below)

# 第三步回归：测试M高于均值一个标准差时的简单斜率
fit_above <- lm(ZDEP ~ ZSS + ZSCABOVE + ZSS_ZSCABOVE, data = data)
summary(fit_above)

M低于均值一个标准差时的回归系数结果

1
2
3
4
5
6
7
8
9
10
11
12
Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept)   0.12906    0.08947   1.442  0.15056   
ZSS           0.98286    0.35601   2.761  0.00623 **
ZSCBELOW     -0.12846    0.06334  -2.028  0.04369 * 
ZSS_ZSCBELOW -0.77388    0.35264  -2.194  0.02920 * 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.9647 on 229 degrees of freedom
Multiple R-squared:  0.08143,	Adjusted R-squared:  0.06939 
F-statistic: 6.767 on 3 and 229 DF,  p-value: 0.0002163

ZSS的斜率系数Estimate为0.98286，Pr(>|t|)为0.00623，表明当社会支持水平低的时候，工作压力对抑郁倾向有显著的正向影响

M高于均值一个标准差时的回归系数结果

1
2
3
4
5
6
7
8
9
10
11
12
Coefficients:
             Estimate Std. Error t value Pr(>|t|)  
(Intercept)  -0.12786    0.08947  -1.429   0.1543  
ZSS          -0.56489    0.36057  -1.567   0.1186  
ZSCABOVE     -0.12846    0.06334  -2.028   0.0437 *
ZSS_ZSCABOVE -0.77388    0.35264  -2.194   0.0292 *
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.9647 on 229 degrees of freedom
Multiple R-squared:  0.08143,	Adjusted R-squared:  0.06939 
F-statistic: 6.767 on 3 and 229 DF,  p-value: 0.0002163

ZSS的斜率系数Estimate为-0.56489，Pr(>|t|)为0.1186，表明当社会支持水平高的时候，工作压力对抑郁倾向的影响不显著

连续变量与分类变量的调节作用

导入包与数据

1
2
3
4
5
6
7
8
9
10
11
12
13
# 导入包
library(haven)
library(psych)
library(lavaan)
library(dplyr)

# 导入数据
setwd("/Users/nanxu/研究生课程作业/心理统计/课件数据/12第十二章 调节效应/")
data <- read_sav("./12_1 mod_1.sav")

# 查看数据
names(data)
dim(data)

虚拟编码后的调教效应检验

虚拟编码与数据预处理

1
2
3
4
# 男性编码为0，女性编码为1
# 转换性别为因子变量
data$SEX = data$SEX - 1
table(data$SEX)  # 查看性别分布
1
2
3
4
5
6
7
8
9
10
11
12
# 中心化变量
data$CSC <- scale(data$SC, scale = FALSE)[, 1]
data$CSS <- scale(data$SS, scale = FALSE)[, 1]

# 标准化变量
data$ZSC <- scale(data$SC)[, 1]
data$ZSS <- scale(data$SS)[, 1]
data$ZDEP <- scale(data$DEP)[, 1]

# 创建交互项
data$GENDERCSS <- data$SEX * data$CSS
data$GENDERZSS <- data$SEX * data$ZSS

非标准化回归系数

对自变量XX进行中心化处理

1
2
3
4
5
6
7
# 非标准化
# 层次回归分析
fit5 <- lm(DEP ~ CSS + SEX, data = data)
summary(fit5)

fit6 <- lm(DEP ~ CSS + SEX + GENDERCSS, data = data)
summary(fit6)

回归系数估计结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
> summary(fit5)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.67996    0.08079  33.172  < 2e-16 ***
CSS          0.33877    0.09301   3.642 0.000334 ***
SEX         -0.24675    0.11518  -2.142 0.033211 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.8687 on 230 degrees of freedom
Multiple R-squared:  0.06445,	Adjusted R-squared:  0.05632 
F-statistic: 7.923 on 2 and 230 DF,  p-value: 0.0004706

> summary(fit6)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.69864    0.08056  33.498  < 2e-16 ***
CSS          0.53737    0.12876   4.173 4.26e-05 ***
SEX         -0.24558    0.11422  -2.150   0.0326 *  
GENDERCSS   -0.40787    0.18452  -2.210   0.0281 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.8615 on 229 degrees of freedom
Multiple R-squared:  0.08399,	Adjusted R-squared:  0.07199 
F-statistic:     7 on 3 and 229 DF,  p-value: 0.0001592

绘制影响图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 绘制影响图
points_data <- data.frame(
  CSS = rep(c(-1, 1), times = 2) * sd(data$CSS),
  SEX = rep(c(0, 1), each = 2)
)
points_data$GENDERCSS <- points_data$CSS * points_data$SEX
points_data$Predicted_DEP <- predict(fit6, newdata = points_data)

plot(points_data$CSS, points_data$Predicted_DEP, type = 'n',
     xlab = "Social Support (Centered)", ylab = "Predicted Depression",
     main = "Effect of Gender and Social Support on Depression")
colors <- c("red", "blue")
for (sex in unique(points_data$SEX)) {
  subset_data <- points_data[points_data$SEX == sex,]
  points(subset_data$CSS, subset_data$Predicted_DEP, col = colors[sex + 1], pch = 19)
  lines(subset_data$CSS, subset_data$Predicted_DEP, col = colors[sex + 1], lwd = 2)
}
legend("topleft", legend = c("Female", "Male"), col = colors, lwd = 2, pch = 19, title = "Gender")

不同性别的工作压力对抑郁倾向的影响

效应量

1
2
3
4
5
6
7
# 假设fit_basic和fit_full已经被拟合
R2_excluded <- summary(fit5)$r.squared  # 基础模型的R^2
R2_included <- summary(fit6)$r.squared   # 完整模型的R^2

# 计算f^2系数
> (R2_included - R2_excluded) / (1 - R2_included)
[1] 0.02133518

标准化回归系数

1
2
3
4
5
6
7
# 标准化
# 层次回归分析
fit7 <- lm(ZDEP ~ ZSS + SEX, data = data)
summary(fit7)

fit8 <- lm(ZDEP ~ ZSS + SEX + GENDERZSS, data = data)
summary(fit8)

回归系数估计结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
> summary(fit7)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.13737    0.09034   1.521 0.129742    
ZSS          0.23506    0.06453   3.642 0.000334 ***
SEX         -0.27592    0.12879  -2.142 0.033211 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.9714 on 230 degrees of freedom
Multiple R-squared:  0.06445,	Adjusted R-squared:  0.05632 
F-statistic: 7.923 on 2 and 230 DF,  p-value: 0.0004706

> summary(fit8)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.15826    0.09008   1.757   0.0803 .  
ZSS          0.37286    0.08934   4.173 4.26e-05 ***
SEX         -0.27461    0.12772  -2.150   0.0326 *  
GENDERZSS   -0.28300    0.12803  -2.210   0.0281 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.9633 on 229 degrees of freedom
Multiple R-squared:  0.08399,	Adjusted R-squared:  0.07199 
F-statistic:     7 on 3 and 229 DF,  p-value: 0.0001592

绘制影响图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 绘制影响图
points_data <- data.frame(
  ZSS = rep(c(-1, 1), times = 2),
  SEX = rep(c(0, 1), each = 2)
)
points_data$GENDERZSS <- points_data$ZSS * points_data$SEX
points_data$Predicted_DEP <- predict(fit8, newdata = points_data)

plot(points_data$ZSS, points_data$Predicted_DEP, type = 'n',
     xlab = "Social Support (Centered)", ylab = "Predicted Depression",
     main = "Effect of Gender and Social Support on Depression")
colors <- c("red", "blue")
for (sex in unique(points_data$SEX)) {
  subset_data <- points_data[points_data$SEX == sex,]
  points(subset_data$ZSS, subset_data$Predicted_DEP, col = colors[sex + 1], pch = 19)
  lines(subset_data$ZSS, subset_data$Predicted_DEP, col = colors[sex + 1], lwd = 2)
}
legend("topleft", legend = c("Female", "Male"), col = colors, lwd = 2, pch = 19, title = "Gender")

不同性别的工作压力对抑郁倾向的影响

简单斜率检验

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 简单斜率检验
# 将性别编码颠倒：原来男性为0，女性为1，现在女性为0，男性为1
data$SEX_N <- ifelse(data$SEX == 0, 1, 0)

# 创建交互项并为性别低于均值一个标准差时的简单斜率添加变量
data$GENDER_NZSS <- data$SEX_N * data$ZSS

# 第一步回归：基本效应模型（没有交互项）
# fit7 <- lm(ZDEP ~ ZSS + SEX, data = data)
summary(fit7)

# 测试性别为男性时的简单斜率
fit_N <- lm(ZDEP ~ ZSS + SEX_N + GENDER_NZSS, data = data)
summary(fit_N)
1
2
3
4
5
6
7
8
9
10
11
12
Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept) -0.11635    0.09054  -1.285   0.2000  
ZSS          0.08986    0.09171   0.980   0.3282  
SEX_N        0.27461    0.12772   2.150   0.0326 *
GENDER_NZSS  0.28300    0.12803   2.210   0.0281 *
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.9633 on 229 degrees of freedom
Multiple R-squared:  0.08399,	Adjusted R-squared:  0.07199 
F-statistic:     7 on 3 and 229 DF,  p-value: 0.0001592

ZSS的斜率系数Estimate为0.08986，Pr(>|t|)为0.3282，表明对于男性，工作压力对抑郁倾向的影响不显著

非加权效应编码后的调节效应检验

非加权效应编码是将分类变量重新编码为-1与+1

非加权效应编码与数据预处理

1
2
3
# 女性编码为-1，男性编码为1
data$SEX_G <- ifelse(data$SEX == 1, 1, -1)
table(data$SEX_G)  # 查看性别分布
1
2
3
4
5
6
7
8
9
10
11
12
# 中心化变量
data$CSC <- scale(data$SC, scale = FALSE)[, 1]
data$CSS <- scale(data$SS, scale = FALSE)[, 1]

# 标准化变量
data$ZSC <- scale(data$SC)[, 1]
data$ZSS <- scale(data$SS)[, 1]
data$ZDEP <- scale(data$DEP)[, 1]

# 创建交互项
data$GENDERCSS <- data$SEX_G * data$CSS
data$GENDERZSS <- data$SEX_G * data$ZSS

非标准化回归系数

1
2
3
4
5
6
7
# 非标准化
# 层次回归分析
fit9 <- lm(DEP ~ CSS + SEX_G, data = data)
summary(fit9)

fit10 <- lm(DEP ~ CSS + SEX_G + GENDERCSS, data = data)
summary(fit10)

回归系数估计结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
> summary(fit9)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.55658    0.05691  44.920  < 2e-16 ***
CSS          0.33877    0.09301   3.642 0.000334 ***
SEX_G       -0.12338    0.05759  -2.142 0.033211 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.8687 on 230 degrees of freedom
Multiple R-squared:  0.06445,	Adjusted R-squared:  0.05632 
F-statistic: 7.923 on 2 and 230 DF,  p-value: 0.0004706

> summary(fit10)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2.57585    0.05711  45.105  < 2e-16 ***
CSS          0.33343    0.09226   3.614 0.000371 ***
SEX_G       -0.12279    0.05711  -2.150 0.032593 *  
GENDERCSS   -0.20393    0.09226  -2.210 0.028069 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.8615 on 229 degrees of freedom
Multiple R-squared:  0.08399,	Adjusted R-squared:  0.07199 
F-statistic:     7 on 3 and 229 DF,  p-value: 0.0001592

绘制影响图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 绘制影响图
points_data <- data.frame(
  CSS = rep(c(-1, 1), times = 2) * sd(data$CSS),
  SEX_G = rep(c(-1, 1), each = 2)
)
points_data$GENDERCSS <- points_data$CSS * points_data$SEX_G
points_data$Predicted_DEP <- predict(fit10, newdata = points_data)

plot(points_data$CSS, points_data$Predicted_DEP, type = 'n',
     xlab = "Social Support (Centered)", ylab = "Predicted Depression",
     main = "Effect of Gender and Social Support on Depression")
colors <- c("red", "blue")
for (sex in unique(points_data$SEX_G)) {
  subset_data <- points_data[points_data$SEX_G == sex,]
  color_index <- ifelse(sex == -1, 2, 1)
  points(subset_data$CSS, subset_data$Predicted_DEP, col = colors[color_index], pch = 19)
  lines(subset_data$CSS, subset_data$Predicted_DEP, col = colors[color_index], lwd = 2)
}
legend("topleft", legend = c("Female", "Male"), col = colors, lwd = 2, pch = 19, title = "Gender")

不同性别的工作压力对抑郁倾向的影响

效应量

1
2
3
4
5
6
7
8
# 效应量
# 假设fit_basic和fit_full已经被拟合
R2_excluded <- summary(fit9)$r.squared  # 基础模型的R^2
R2_included <- summary(fit10)$r.squared   # 完整模型的R^2

# 计算f^2系数
> (R2_included - R2_excluded) / (1 - R2_included)
[1] 0.02133518

标准化回归系数

1
2
3
4
5
6
7
# 标准化
# 层次回归分析
fit11 <- lm(ZDEP ~ ZSS + SEX_G, data = data)
summary(fit11)

fit12 <- lm(ZDEP ~ ZSS + SEX_G + GENDERZSS, data = data)
summary(fit12)

回归系数估计结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
> summary(fit11)

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -0.0005921  0.0636413  -0.009 0.992585    
ZSS          0.2350608  0.0645333   3.642 0.000334 ***
SEX_G       -0.1379606  0.0643952  -2.142 0.033211 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.9714 on 230 degrees of freedom
Multiple R-squared:  0.06445,	Adjusted R-squared:  0.05632 
F-statistic: 7.923 on 2 and 230 DF,  p-value: 0.0004706

> summary(fit12)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.02095    0.06386   0.328 0.743123    
ZSS          0.23136    0.06402   3.614 0.000371 ***
SEX_G       -0.13730    0.06386  -2.150 0.032593 *  
GENDERZSS   -0.14150    0.06402  -2.210 0.028069 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.9633 on 229 degrees of freedom
Multiple R-squared:  0.08399,	Adjusted R-squared:  0.07199 
F-statistic:     7 on 3 and 229 DF,  p-value: 0.0001592

绘制影响图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 绘制影响图
points_data <- data.frame(
  ZSS = rep(c(-1, 1), times = 2),
  SEX_G = rep(c(-1, 1), each = 2)
)
points_data$GENDERZSS <- points_data$ZSS * points_data$SEX
points_data$Predicted_DEP <- predict(fit12, newdata = points_data)

plot(points_data$ZSS, points_data$Predicted_DEP, type = 'n',
     xlab = "Social Support (Centered)", ylab = "Predicted Depression",
     main = "Effect of Gender and Social Support on Depression")
colors <- c("red", "blue")
for (sex in unique(points_data$SEX_G)) {
  subset_data <- points_data[points_data$SEX_G == sex,]
  color_index <- ifelse(sex == -1, 2, 1)
  points(subset_data$ZSS, subset_data$Predicted_DEP, col = colors[color_index], pch = 19)
  lines(subset_data$ZSS, subset_data$Predicted_DEP, col = colors[color_index], lwd = 2)
}
legend("topleft", legend = c("Female", "Male"), col = colors, lwd = 2, pch = 19, title = "Gender")

不同性别的工作压力对抑郁倾向的影响

简单斜率检验

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 简单斜率检验
# 将性别编码颠倒：原来男性为1，女性为-1，现在女性为-1，男性为1
data$SEX_GN <- ifelse(data$SEX_G == -1, 1, -1)

# 创建交互项并为性别低于均值一个标准差时的简单斜率添加变量
data$GENDER_NZSS <- data$SEX_GN * data$ZSS

# 第一步回归：基本效应模型（没有交互项）
# fit11 <- lm(ZDEP ~ ZSS + SEX_G, data = data)
summary(fit11)

# 测试性别为男性时的简单斜率
fit_N <- lm(ZDEP ~ ZSS + SEX_GN + GENDER_NZSS, data = data)
summary(fit_N)
1
2
3
4
5
6
7
8
9
10
11
12
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.02095    0.06386   0.328 0.743123    
ZSS          0.23136    0.06402   3.614 0.000371 ***
SEX_GN       0.13730    0.06386   2.150 0.032593 *  
GENDER_NZSS  0.14150    0.06402   2.210 0.028069 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.9633 on 229 degrees of freedom
Multiple R-squared:  0.08399,	Adjusted R-squared:  0.07199 
F-statistic:     7 on 3 and 229 DF,  p-value: 0.0001592

ZSS的斜率系数Estimate为0.23136，Pr(>|t|)为0.000371，表明对于男性，工作压力对抑郁倾向的影响显著

潜变量的调节效应

潜变量与分类变量的调节效应分析

导入包与数据

1
2
3
4
5
6
7
8
9
10
11
# 导入包
library(haven)
library(lavaan)

# 导入数据
setwd("/Users/nanxu/研究生课程作业/心理统计/课件数据/12第十二章 调节效应/")
data <- read_sav("./12_2 mod_2.sav")

# 查看数据
names(data)
dim(data)

数据分组与介绍

1
2
3
4
data$sex <- factor(data$sex, levels = c(1, 2), labels = c("female", "male"))

# 描述数据
summary(data)

结构方程模型

1
2
3
4
5
6
7
8
model <- '
  # 测量模型
  DEP =~ Y1 + Y2 + Y3
  STRESS =~ X1 + X2 + X3
  
  # 结构模型
  DEP ~ STRESS
'

结构等价性

1
2
3
# 结构等价性
fit1 <- sem(model, data = data, group = "sex")
summary(fit1, standardized = TRUE, fit.measures = TRUE, rsquare=TRUE)

模型拟合结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Model Test User Model:
                                                      
  Test statistic                                21.888
  Degrees of freedom                                16
  P-value (Chi-square)                           0.147
  Test statistic for each group:
    male                                        16.217
    female                                       5.671

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.985
  Tucker-Lewis Index (TLI)                       0.971

Root Mean Square Error of Approximation:

  RMSEA                                          0.045
  90 Percent confidence interval - lower         0.000
  90 Percent confidence interval - upper         0.087
  P-value H_0: RMSEA <= 0.050                    0.533
  P-value H_0: RMSEA >= 0.080                    0.093

可以看出RMSEA值为0.045，CFI的值为0.985，TLI的值为0.971，表明模型拟合较好，男女两组满足因子结构等价性。

弱等价性

1
2
3
4
# 弱等价性
fit2 <- sem(model, data = data, group = "sex", group.equal = "loadings")
summary(fit2, fit.measures = TRUE, standardized = TRUE, rsquare=TRUE)
anova(fit1, fit2)
1
2
3
4
5
6
7
> anova(fit1, fit2)

Chi-Squared Difference Test

     Df    AIC    BIC  Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
fit1 16 5916.4 6064.8 21.888                                    
fit2 20 5910.7 6043.5 24.225     2.3363     0       4     0.6742

可以看出两个模型的卡方值的差值Chisq diff为2.3363，自由度的差值Df diff为4，表明两个模型的卡方差异不显著。可以接受弱等价模型，即认为男女两组满足因素载荷等价条件。

结构方程系数等价性

1
2
3
4
# 回归系数等价性
fit3 <- sem(model, data = data, group = "sex", group.equal = c("regressions", "loadings"))
summary(fit3, fit.measures = TRUE, standardized = TRUE, rsquare=TRUE)
anova(fit1, fit2, fit3)
1
2
3
4
5
6
7
8
> anova(fit1, fit2, fit3)

Chi-Squared Difference Test

     Df    AIC    BIC  Chisq Chisq diff   RMSEA Df diff Pr(>Chisq)  
fit1 16 5916.4 6064.8 21.888                                        
fit2 20 5910.7 6043.5 24.225     2.3363 0.00000       4    0.67416  
fit3 21 5911.8 6040.7 27.317     3.0923 0.10678       1    0.07866 .

可以看出两个模型的卡方值的差值Chisq diff为3.0923，自由度的差值Df diff为1，表明两个模型的卡方差异不显著。可以接受潜变量路径系数等价模型，即认为男女两组满足路径系数等价条件。即性别在压力对抑郁的影响中的调节作用不显著。

潜变量与潜变量的调节效应分析

导入包与数据

1
2
3
4
5
6
7
8
9
10
11
# 导入包
library(haven)
library(lavaan)

# 导入数据
setwd("/Users/nanxu/研究生课程作业/心理统计/课件数据/12第十二章 调节效应/")
data <- read_sav("./12_6 mod_3.sav")

# 查看数据
names(data)
dim(data)

数据介绍与数据预处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 描述数据
summary(data)

# 中心化变量
data$CCON1 <- scale(data$CON1, scale = FALSE)[, 1]
data$CCON2 <- scale(data$CON2, scale = FALSE)[, 1]
data$CCON3 <- scale(data$CON3, scale = FALSE)[, 1]
data$CCON4 <- scale(data$CON4, scale = FALSE)[, 1]
data$CDEP1 <- scale(data$DEP1, scale = FALSE)[, 1]
data$CDEP2 <- scale(data$DEP2, scale = FALSE)[, 1]
data$CDEP3 <- scale(data$DEP3, scale = FALSE)[, 1]
data$CDEP4 <- scale(data$DEP4, scale = FALSE)[, 1]

# 乘积指标
data$CCON1CDEP1 <- data$CCON1 * data$CDEP1
data$CCON2CDEP2 <- data$CCON2 * data$CDEP2
data$CCON3CDEP3 <- data$CCON3 * data$CDEP3
data$CCON4CDEP4 <- data$CCON4 * data$CDEP4

# 乘积指标二次中心化
data$C_CCON1CDEP1 <- scale(data$CCON1CDEP1, scale = FALSE)[, 1]
data$C_CCON2CDEP2 <- scale(data$CCON2CDEP2, scale = FALSE)[, 1]
data$C_CCON3CDEP3 <- scale(data$CCON3CDEP3, scale = FALSE)[, 1]
data$C_CCON4CDEP4 <- scale(data$CCON4CDEP4, scale = FALSE)[, 1]

乘积指标法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
model <- '
  # 测量模型
  CON =~ CCON1 + CCON2 + CCON3 + CCON4
  DEP =~ CDEP1 + CDEP2 + CDEP3 + CDEP4
  CONDEP =~ C_CCON1CDEP1 + C_CCON2CDEP2 + C_CCON3CDEP3 + C_CCON4CDEP4
  
  # 结构模型
  ALC ~ CON + DEP + CONDEP
  
  # 显示截距
  ALC ~ 1
'

fit <- sem(model, data = data, estimator = "ML")
summary(fit, standardized = TRUE, fit.measures = TRUE, rsquare=TRUE)

绘制影响图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 绘制影响图
points_data <- data.frame(
  CON = rep(c(-1, 1), each = 5) * sqrt(coef(fit)["CON~~CON"]),
  DEP = rep(c(-2, -1, 0, 1, 2), times = 2) * sqrt(coef(fit)["DEP~~DEP"])
)
points_data$CONDEP <- points_data$CON * points_data$DEP
calculate_ALC <- function(df) {
  ALC = coef(fit)["ALC~1"] + coef(fit)["ALC~CON"] * df$CON + coef(fit)["ALC~DEP"] * df$DEP + coef(fit)["ALC~CONDEP"] * df$CONDEP
  return(ALC)
}
points_data$Predicted_ALC <- calculate_ALC(points_data)

plot(points_data$CON, points_data$Predicted_ALC, type = 'n',
     xlab = "CON", ylab = "pre_ALC",
     main = "Effect of DEP and CON on ALC")
colors <- c("red", "blue", "green", "yellow", "black")
points_data$DEP_index <- points_data$DEP/sqrt(coef(fit)["DEP~~DEP"]) *abs(points_data$CON)/sqrt(coef(fit)["CON~~CON"]) + 3
# 使用新的变量来索引颜色
for (index in unique(points_data$DEP_index)) {
  subset_data <- points_data[points_data$DEP_index == index,]
  points(subset_data$CON, subset_data$Predicted_ALC, col = colors[index], pch = 19)
  lines(subset_data$CON, subset_data$Predicted_ALC, col = colors[index], lwd = 2)
}
legend("topleft", legend = c(-2, -1, 0, 1, 2), col = colors, lwd = 2, pch = 19, title = "DEP")

在不同的抑郁症状水平上，问题行为对饮酒行为对影响

潜调节结构方程

导入包与数据

1
2
3
4
5
6
7
8
9
10
11
# 导入包
library(haven)
library(lavaan)

# 导入数据
setwd("/Users/nanxu/研究生课程作业/心理统计/课件数据/12第十二章 调节效应/")
data <- read_sav("./12_6 mod_3.sav")

# 查看数据
names(data)
dim(data)

描述数据与数据预处理

1
2
3
4
5
# 描述数据
summary(data)

# 标准化数据
data[, c("CCON1", "CCON2", "CCON3", "CCON4", "CDEP1", "CDEP2", "CDEP3", "CDEP4", "CALC")] <- scale(data[, c("CON1", "CON2", "CON3", "CON4", "DEP1", "DEP2", "DEP3", "DEP4", "ALC")])

基准模型0

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 模型0
model0 <- '
  # 测量模型
  CCON =~ CCON1 + CCON2 + CCON3 + CCON4
  CDEP =~ CDEP1 + CDEP2 + CDEP3 + CDEP4
  
  # 关联
  CCON ~~ CDEP
  
  # 结构模型
  CALC ~ CCON + CDEP
'

# 运行模型
fit0 <- sem(model0, data = data, estimator = "ML")
summary(fit0, standardized = TRUE, fit.measures = TRUE, rsquare=TRUE)

modsem方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 模型1
library(modsem)
model1 <- '
  # 测量模型
  CON =~ CON1 + CON2 + CON3 + CON4
  DEP =~ DEP1 + DEP2 + DEP3 + DEP4
  
  # 关联
  #CON ~~ DEP

  # 结构模型
  ALC ~ a*CON + b*DEP + c*CON:DEP
'

fit1 <- modsem(model1, data = data, method = "lms")
summary(fit1, standardized = TRUE, fit.measures = TRUE, rsquare=TRUE)

nlsem方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 创建模型方法1
lav_model <- '
  # 测量模型
  xi1 =~ x1 + x2 + x3 + x4
  xi2 =~ x5 + x6 + x7 + x8
  eta =~ y1
  
  eta ~ xi1 + xi2 + xi1:xi2
'
model1 <- lav2nlsem(lav_model)

# 创建模型方法2
model1 <- specify_sem(
  num.x = 8,              # 指标变量数量，用于xi（这里认为是CCON的指标）
  num.y = 1,              # 指标变量数量，用于eta（这里认为是CDEP的指标）
  num.xi = 2,             # 潜在外生变量的数量（CCON）
  num.eta = 1,            # 潜在内生变量的数量（CDEP）
  xi = "x1-x4, x5-x8",           # 指标变量 x1 至 x4 是 CCON 的指标
  eta = "y1",          # 指标变量 y1 至 y4 是 CDEP 的指标
  interaction = "xi1:xi2", # 交互项 CDEP (eta) 和 CCON (xi)
  rel.lat = "default"    # 定义潜变量之间的关系
)

# 随机生成起始值
set.seed(666)
start <- runif(count_free_parameters(model1))

# 拟合模型
fit1 <- em(model1, as.matrix(data[, c(10:18)]), start, convergence = 0.01, max.iter = 200)

# 检查结果
summary(fit1)
plot(fit1)

有调节的中介

导入包与数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 导入包
library(haven)
library(lavaan)
library(blavaan)

# 导入数据
setwd("/Users/nanxu/研究生课程作业/心理统计/课件数据/12第十二章 调节效应/")
data <- read_sav("./12_12 mod_med.sav")

# 查看数据
names(data)
dim(data)

# 描述数据
summary(data)

简单调节模型

1
2
3
4
5
6
7
8
9
10
11
# 简单调节模型
model1 <- '
  # 回归方程
  SAT ~ CPREL + SIZE + CPRELSIZE
'

# 拟合模型
fit1 <- sem(model1, data = data)

# 查看模型摘要
summary(fit1, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE)

参数估计结果与标准化参数估计结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
Regressions:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  SAT ~                                                                 
    CPREL             0.244    0.096    2.550    0.011    0.244    0.222
    SIZE             -0.229    0.162   -1.419    0.156   -0.229   -0.085
    CPRELSIZE         0.038    0.132    0.290    0.772    0.038    0.025

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .SAT               1.685    0.148   11.402    0.000    1.685    0.938

R-Square:
                   Estimate
    SAT               0.062

可以看出积极的劳资关系压力PREL对工作满意度SAT的效应显著，P(>|z|)为0.011。但是积极的劳资关系压力与企业规模的交互项CPRELSIZE对工作满意度SAT的效应不显著，P(>|z|)为0.772。因此，积极的劳资关系压力PREL对工作满意度SAT的直接效应不受调节。

有调节的中介效应检验

系数依次检验

1
2
3
4
5
6
7
8
9
10
11
12
# 有调节的中介
model2 <- '
  # 回归方程
  SAT ~ PEM + CPREL
  PEM ~ CPREL + CPRELSIZE + SIZE
'

# 拟合模型
fit2 <- sem(model2, data = data)

# 查看模型摘要
summary(fit2, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE)

模型拟合结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
Model Test User Model:
                                                      
  Test statistic                                 2.598
  Degrees of freedom                                 2
  P-value (Chi-square)                           0.273

Model Test Baseline Model:

  Test statistic                               225.874
  Degrees of freedom                                 7
  P-value                                        0.000

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.997
  Tucker-Lewis Index (TLI)                       0.990

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)               -761.932
  Loglikelihood unrestricted model (H1)             NA
                                                      
  Akaike (AIC)                                1537.865
  Bayesian (BIC)                              1562.790
  Sample-size adjusted Bayesian (SABIC)       1540.597

Root Mean Square Error of Approximation:

  RMSEA                                          0.034
  90 Percent confidence interval - lower         0.000
  90 Percent confidence interval - upper         0.133
  P-value H_0: RMSEA <= 0.050                    0.477
  P-value H_0: RMSEA >= 0.080                    0.299

Standardized Root Mean Square Residual:

  SRMR                                           0.016

可以看出，卡方值为2.598，自由度为2，CFI值为0.997，TLI值为0.990，RMSEA值为0.034，表明模型拟合较好。

参数估计结果与标准化参数估计结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Regressions:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  SAT ~                                                                 
    PEM               0.225    0.065    3.473    0.001    0.225    0.211
    CPREL             0.199    0.067    2.970    0.003    0.199    0.181
  PEM ~                                                                 
    CPREL             0.428    0.063    6.757    0.000    0.428    0.416
    CPRELSIZE        -0.227    0.088   -2.578    0.010   -0.227   -0.158
    SIZE             -1.710    0.107  -15.942    0.000   -1.710   -0.679

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .SAT               1.623    0.142   11.402    0.000    1.623    0.904
   .PEM               0.741    0.065   11.402    0.000    0.741    0.469

R-Square:
                   Estimate
    SAT               0.096
    PEM               0.531

可以看出所有的路径都显著，PEM ~ CPREL的路径系数为0.428，PEM ~ CPRELSIZE的路径系数为-0.227，SAT ~ PEM的路径系数为0.225，依次检验的结果显著，足以证明中介效应是收到调节的。

乘积系数的区间检验

1
2
3
4
5
6
7
8
9
# 定义模型
model3 <- '
  # 回归方程
  PEM ~ a1*CPREL + a2*SIZE + a3*CPRELSIZE 
  SAT ~ c*PEM + b*CPREL
  
  # 中介效应
  h1 := a3*b  # z=0 和 z=1 时中介效应的差值
'
偏差校正的Bootstrap方法
1
2
3
4
5
6
7
8
9
10
# 使用 bootstrap 进行拟合
fit_bootstrap <- sem(model3, data = data, se = "bootstrap", bootstrap = 2000)

# 查看模型摘要，包括偏差修正的 bootstrap 置信区间
summary(fit_bootstrap, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE, ci = TRUE)

# 查看参数估计，包括不同置信水平的偏差修正的 bootstrap 置信区间
parameterEstimates(fit_bootstrap, level = 0.90, boot.ci.type = "bca.simple")
parameterEstimates(fit_bootstrap, level = 0.95, boot.ci.type = "bca.simple")
parameterEstimates(fit_bootstrap, level = 0.99, boot.ci.type = "bca.simple")

参数估计结果与标准化参数估计结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Regressions:
                   Estimate  Std.Err  z-value  P(>|z|) ci.lower ci.upper   Std.lv  Std.all
  PEM ~                                                                                   
    CPREL     (a1)    0.428    0.065    6.633    0.000    0.294    0.553    0.428    0.416
    SIZE      (a2)   -1.710    0.103  -16.522    0.000   -1.911   -1.505   -1.710   -0.679
    CPRELSIZE (a3)   -0.227    0.086   -2.622    0.009   -0.389   -0.051   -0.227   -0.158
  SAT ~                                                                                   
    PEM        (c)    0.225    0.067    3.338    0.001    0.089    0.357    0.225    0.211
    CPREL      (b)    0.199    0.073    2.717    0.007    0.051    0.345    0.199    0.181

Variances:
                   Estimate  Std.Err  z-value  P(>|z|) ci.lower ci.upper   Std.lv  Std.all
   .PEM               0.741    0.054   13.708    0.000    0.627    0.839    0.741    0.469
   .SAT               1.623    0.114   14.260    0.000    1.388    1.833    1.623    0.904

R-Square:
                   Estimate
    PEM               0.531
    SAT               0.096

Defined Parameters:
                   Estimate  Std.Err  z-value  P(>|z|) ci.lower ci.upper   Std.lv  Std.all
    h1               -0.045    0.025   -1.825    0.068   -0.100   -0.005   -0.045   -0.029

90%置信区间、95%置信区间、99%置信区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
> parameterEstimates(fit_bootstrap, level = 0.90, boot.ci.type = "bca.simple")
         lhs op       rhs label    est    se       z pvalue ci.lower ci.upper
1        PEM  ~     CPREL    a1  0.428 0.065   6.633  0.000    0.317    0.529
2        PEM  ~      SIZE    a2 -1.710 0.103 -16.522  0.000   -1.883   -1.541
3        PEM  ~ CPRELSIZE    a3 -0.227 0.086  -2.622  0.009   -0.362   -0.078
4        SAT  ~       PEM     c  0.225 0.067   3.338  0.001    0.114    0.338
5        SAT  ~     CPREL     b  0.199 0.073   2.717  0.007    0.078    0.319
14        h1 :=      a3*b    h1 -0.045 0.025  -1.825  0.068   -0.096   -0.013

> parameterEstimates(fit_bootstrap, level = 0.95, boot.ci.type = "bca.simple")
         lhs op       rhs label    est    se       z pvalue ci.lower ci.upper
1        PEM  ~     CPREL    a1  0.428 0.065   6.633  0.000    0.293    0.551
2        PEM  ~      SIZE    a2 -1.710 0.103 -16.522  0.000   -1.913   -1.508
3        PEM  ~ CPRELSIZE    a3 -0.227 0.086  -2.622  0.009   -0.389   -0.050
4        SAT  ~       PEM     c  0.225 0.067   3.338  0.001    0.093    0.360
5        SAT  ~     CPREL     b  0.199 0.073   2.717  0.007    0.050    0.344
14        h1 :=      a3*b    h1 -0.045 0.025  -1.825  0.068   -0.107   -0.008

> parameterEstimates(fit_bootstrap, level = 0.99, boot.ci.type = "bca.simple")
         lhs op       rhs label    est    se       z pvalue ci.lower ci.upper
1        PEM  ~     CPREL    a1  0.428 0.065   6.633  0.000    0.249    0.583
2        PEM  ~      SIZE    a2 -1.710 0.103 -16.522  0.000   -1.979   -1.455
3        PEM  ~ CPRELSIZE    a3 -0.227 0.086  -2.622  0.009   -0.453   -0.002
4        SAT  ~       PEM     c  0.225 0.067   3.338  0.001    0.054    0.407
5        SAT  ~     CPREL     b  0.199 0.073   2.717  0.007    0.010    0.386
14        h1 :=      a3*b    h1 -0.045 0.025  -1.825  0.068   -0.137    0.000

可以看出乘积系数h1 = a3*b的95%置信区间为[-0.100 ,-0.005]，不包含0，表明积极的劳资关系压力PREL通过积极情绪PEM对工作满意度SAT的中介效应的前半路径收到企业规模SIZE的调节作用。

MCMC方法
1
2
3
4
5
# 使用贝叶斯估计进行拟合
fit_bayes <- bsem(model, data = data, n.chains = 2, burnin = 10000, sample = 30000)

# 查看模型摘要
summary(fit_bayes, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Regressions:
                   Estimate  Post.SD pi.lower pi.upper   Std.lv  Std.all     Rhat    Prior       
  PEM ~                                                                                          
    CPREL     (a1)    0.429    0.064    0.304    0.556    0.429    0.414    1.000    normal(0,10)
    SIZE      (a2)   -1.709    0.109   -1.921   -1.497   -1.709   -0.675    1.000    normal(0,10)
    CPRELSIZE (a3)   -0.228    0.089   -0.403   -0.053   -0.228   -0.158    1.000    normal(0,10)
  SAT ~                                                                                          
    PEM        (c)    0.225    0.065    0.097    0.354    0.225    0.211    1.000    normal(0,10)
    CPREL      (b)    0.199    0.068    0.066    0.332    0.199    0.179    1.000    normal(0,10)

Variances:
                   Estimate  Post.SD pi.lower pi.upper   Std.lv  Std.all     Rhat    Prior       
   .PEM               0.758    0.067    0.638    0.901    0.758    0.474    1.000 gamma(1,.5)[sd]
   .SAT               1.651    0.147    1.387    1.965    1.651    0.905    1.000 gamma(1,.5)[sd]

R-Square:
                   Estimate
    PEM               0.526
    SAT               0.095

Defined Parameters:
                   Estimate  Post.SD pi.lower pi.upper   Std.lv  Std.all     Rhat    Prior       
    h1               -0.045    0.024   -0.093    0.002   -0.045   -0.028

可以看出乘积系数h1 = a3*b的95%置信区间为[-0.093 ,0.002]，包含0，表明积极的劳资关系压力PREL通过积极情绪PEM对工作满意度SAT的中介效应的前半路径收到企业规模SIZE的调节作用不显著。

多层线性模型

多水平分析简化模型类型

导入包与数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 导入包
library(haven)
library(psych)
library(lme4)
library(performance)
library(lmerTest)
library(parameters)

# 导入数据
setwd("/Users/nanxu/研究生课程作业/心理统计/课件数据/13第十三章 多层线性模型简介/")
data1 <- read_sav("./13-1.SAV")
data2 <- read_sav("./13-2.SAV")

# 查看数据
names(data1)
dim(data1)
names(data2)
dim(data2)

数据介绍及数据合并

1
2
3
4
5
6
7
8
9
10
11
12
13
# 描述数据
describe(data1)
describe(data2)

table(data1$id)
table(data2$id)

table(unique(data1$id) == data2$id)

# 合并数据
merged_data <- merge(data1, data2, by = "id")
names(merged_data)
dim(merged_data)

零模型

1
2
3
4
5
6
# 拟合零模型
model1 <- lmer(mathach ~ 1 + (1 | id), data = merged_data)
summary(model1, standardized=TRUE)

# 计算组间变异占总变异的比例（解释率）
icc(model1)

固定部分参数估计结果

1
2
3
Fixed effects:
            Estimate Std. Error       df t value Pr(>|t|)    
(Intercept)  12.6370     0.2444 156.6473   51.71   <2e-16 ***

从固定部分参数可以看出，学校之间的数学成绩是存在显著差异的，γ00\gamma _{00}为12.6370，Pr(>|t|) <2e-16。

随机部分参数估计结果

1
2
3
4
5
Random effects:
 Groups   Name        Variance Std.Dev.
 id       (Intercept)  8.614   2.935   
 Residual             39.148   6.257   
Number of obs: 7185, groups:  id, 160

从随机部分的参数可以看出，学校之间数学成绩存在显著的变异，τ00\tau _{00}为8.614

组间变异占总变异的比例

1
2
3
4
5
> icc(model1)
# Intraclass Correlation Coefficient

    Adjusted ICC: 0.180
  Unadjusted ICC: 0.180

表明学校间的变异解释了总体变异的18.0%

随机效应单因素协方差分析模型

1
2
3
# 随机效应单因素协方差分析模型
model1_2 <- lmer(mathach ~ 1 + (1 | id) + ses, data = merged_data)
summary(model1_2, standardized=TRUE)

固定部分参数估计结果

1
2
3
4
Fixed effects:
             Estimate Std. Error        df t value Pr(>|t|)    
(Intercept)   12.6575     0.1880  148.3022   67.33   <2e-16 ***
ses            2.3902     0.1057 6838.0776   22.61   <2e-16 ***

随机部分参数估计结果

1
2
3
4
5
Random effects:
 Groups   Name        Variance Std.Dev.
 id       (Intercept)  4.768   2.184   
 Residual             37.034   6.086   
Number of obs: 7185, groups:  id, 160

随机系数回归模型

1
2
3
# 第一水平加入ses的随机系数回归模型
model2 <- lmer(mathach ~ ses + (ses | id), data = merged_data)
summary(model2, standardized=TRUE)

固定部分参数估计结果

1
2
3
4
Fixed effects:
            Estimate Std. Error       df t value Pr(>|t|)    
(Intercept)  12.6650     0.1898 145.5479   66.71   <2e-16 ***
ses           2.3938     0.1181 157.5299   20.27   <2e-16 ***

从固定部分参数可以看出，社会经济地位ses对数学成绩mathach有显著影响，γ10\gamma _{10}为2.3938，Pr(>|t|) <2e-16。

随机部分参数估计结果

1
2
3
4
5
6
Random effects:
 Groups   Name        Variance Std.Dev. Corr 
 id       (Intercept)  4.8287  2.1974        
          ses          0.4129  0.6426   -0.11
 Residual             36.8301  6.0688        
Number of obs: 7185, groups:  id, 160

从随机部分的参数可以看出，第一水平的截距(τ00\tau _{00}为4.8287)和斜率(τ11\tau _{11}为0.4129)

第二水平仅截距项含有预测变量的随机系数回归模型

1
2
3
# 第二水平仅截距项含有预测变量disclim的随机系数回归模型
model3 <- lmer(mathach ~ ses + disclim + (ses | id), data = merged_data)
summary(model3, standardized=TRUE)

固定部分参数估计结果

1
2
3
4
5
Fixed effects:
            Estimate Std. Error       df t value Pr(>|t|)    
(Intercept)  12.5783     0.1718 141.8784  73.202  < 2e-16 ***
ses           2.3877     0.1185 157.7795  20.151  < 2e-16 ***
disclim      -1.2492     0.1765 156.4273  -7.076 4.69e-11 ***

从固定部分参数可以看出，学校纪律环境disclim对数学成绩mathach有显著影响，γ01\gamma _{01}为-1.2492，Pr(>|t|) <4.69e-11。

随机部分参数估计结果

1
2
3
4
5
Random effects:
 Groups   Name        Variance Std.Dev. Corr
 id       (Intercept)  3.7840  1.9452       
          ses          0.4497  0.6706   0.36
 Residual             36.7954  6.0659

第二水平仅截距项含有预测变量的随机系数回归模型(全模型)

1
2
3
4
# 第二水平含有预测变量disclim的随机系数回归模型（全模型）
model4 <- lmer(mathach ~ ses + disclim + ses * disclim + (ses | id), data = merged_data)
summary(model4, standardized=TRUE)
calculate_explained_variance(model3, model4, 2, 5)

固定部分参数估计结果

1
2
3
4
5
6
Fixed effects:
             Estimate Std. Error        df t value Pr(>|t|)    
(Intercept)   12.6653     0.1703  147.7224  74.353  < 2e-16 ***
ses            2.4074     0.1060 2979.5968  22.721  < 2e-16 ***
disclim       -1.1262     0.1762  151.2579  -6.391 1.93e-09 ***
ses:disclim    0.5735     0.1135 2497.9943   5.054 4.65e-07 ***

从固定部分参数可以看出，学校纪律环境disclim对社会经济地位ses和数学成绩mathach之间对关系具有显著的调节作用，γ11\gamma _{11}为0.5735，Pr(>|t|) <4.65e-07。

随机部分参数估计结果

1
2
3
4
5
6
Random effects:
 Groups   Name        Variance Std.Dev. Corr
 id       (Intercept)  3.71623 1.9278       
          ses          0.02828 0.1682   1.00
 Residual             36.86953 6.0720       
Number of obs: 7185, groups:  id, 160

多层线性模型分析追踪数据

个体特征随时间变化的趋势

导入包与数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 导入包
library(haven)
library(psych)
library(lme4)

# 导入数据
setwd("/Users/nanxu/研究生课程作业/心理统计/课件数据/14第十四章 多层线性模型在追踪研究中的应用/")
data1 <- read_sav("./14-1.sav")
data2 <- read_sav("./14-2.sav")

# 查看数据
names(data1)
dim(data1)
names(data2)
dim(data2)

数据介绍与数据合并

1
2
3
4
5
6
7
8
9
10
# 描述数据
describe(data1)
describe(data2)

table(unique(data1$ID) == data2$ID)

# 合并数据
merged_data <- merge(data1, data2, by = "ID")
names(merged_data)
dim(merged_data)

线性增长模型

无条件均值模型
1
2
3
4
5
6
# 无条件均值模型零模型
model1 <- lmer(SELF ~ 1 + (1 | ID), data = merged_data)
summary(model1, standardized=TRUE)

# 计算组间变异占总变异的比例（解释率）
icc(model1)

固定部分参数估计结果

1
2
3
Fixed effects:
             Estimate Std. Error        df t value Pr(>|t|)    
(Intercept)   2.69007    0.02226 263.00000   120.8   <2e-16 ***

随机部分参数估计结果

1
2
3
4
5
Random effects:
 Groups   Name        Variance Std.Dev.
 ID       (Intercept) 0.09694  0.3114  
 Residual             0.13568  0.3683  
Number of obs: 1056, groups:  ID, 264

个体间变异占总变异的比例

1
2
3
4
5
> icc(model1)
# Intraclass Correlation Coefficient

    Adjusted ICC: 0.417
  Unadjusted ICC: 0.417
无条件增长模型
1
2
3
# 无条件增长模型
model2 <- lmer(SELF ~ TIME + (TIME | ID), data = merged_data)
summary(model2, standardized=TRUE)

固定部分参数估计结果

1
2
3
4
Fixed effects:
             Estimate Std. Error        df t value Pr(>|t|)    
(Intercept)   2.81608    0.02137 262.99975 131.804  < 2e-16 ***
TIME         -0.08401    0.01162 262.99948  -7.228 5.31e-12 ***

随机部分参数估计结果

1
2
3
4
5
6
Random effects:
 Groups   Name        Variance Std.Dev. Corr
 ID       (Intercept) 0.05258  0.2293       
          TIME        0.01625  0.1275   0.20
 Residual             0.09705  0.3115       
Number of obs: 1056, groups:  ID, 264
全模型
1
2
3
# 全模型
model3 <- lmer(SELF ~ TIME + TIME*GENDER + TIME*WITHDRAW + (TIME | ID), data = merged_data)
summary(model3, standardized=TRUE)

固定部分参数估计结果

1
2
3
4
5
6
7
8
Fixed effects:
                Estimate Std. Error         df t value Pr(>|t|)    
(Intercept)     2.813817   0.031052 260.998678  90.617  < 2e-16 ***
TIME           -0.116611   0.017290 260.999768  -6.744 9.85e-11 ***
GENDER          0.004017   0.041401 260.998678   0.097  0.92278    
WITHDRAW       -0.104416   0.020567 260.998677  -5.077 7.30e-07 ***
TIME:GENDER     0.057760   0.023052 260.999768   2.506  0.01283 *  
TIME:WITHDRAW   0.032042   0.011452 260.999769   2.798  0.00553 **

从固定部分参数可以看出，对于第一水平的截距，在控制性别和初始退缩行为后，初始自我概念的均值(Intercept)为β00\beta _{00}为2.813817，初始状态男女生自我概念的均值GENDER不存在显著差异(β01\beta _{01}为0.004017，Pr(>|t|) 为0.92278)，初始退缩行为WITHDRAW对初始的自我概念SELF有负向的预测作用(β02\beta _{02}为-0.104416，Pr(>|t|)为7.30e-07)；对于第一水平斜率，在控制了性别与初始退缩行为影响后，从时间TIME上依然有明显的下降趋势(β10\beta _{10}为-0.116611，Pr(>|t|)为9.85e-11)，男生的自我概念要比女生的自我概念下降的速度TIME:GENDER慢(β11\beta _{11}为0.057760，Pr(>|t|)为0.01283)，退缩行为严重的儿童自我概念下降也较为缓慢(β12\beta _{12}为0.032042，Pr(>|t|)为0.00553)

随机部分参数估计结果

1
2
3
4
5
6
Random effects:
 Groups   Name        Variance Std.Dev. Corr
 ID       (Intercept) 0.04247  0.2061       
          TIME        0.01482  0.1217   0.35
 Residual             0.09705  0.3115       
Number of obs: 1056, groups:  ID, 264

非线性增长模型

1
2
3
# 非线性增长模型
model4 <- lmer(SELF ~ TIME + TIME2 + (TIME | ID) + (TIME2 | ID), data = merged_data)
summary(model4, standardized=TRUE)

固定部分参数估计结果

1
2
3
4
5
Fixed effects:
              Estimate Std. Error         df t value Pr(>|t|)    
(Intercept)   2.852225   0.022981 359.215039 124.114  < 2e-16 ***
TIME         -0.192433   0.030473 642.042214  -6.315 5.05e-10 ***
TIME2         0.036140   0.009452 539.663802   3.823 0.000147 ***

从固定部分参数可以看出，从时间上自我概念有显著的二次型变化趋势TIME2(β20\beta _{20}为0.036140，Pr(>|t|)为0.000147)

随机部分参数估计结果

1
2
3
4
5
6
7
Random effects:
 Groups   Name        Variance  Std.Dev. Corr 
 ID       (Intercept) 0.0099524 0.09976       
          TIME        0.0156733 0.12519  1.00 
 ID.1     (Intercept) 0.0404869 0.20121       
          TIME2       0.0001715 0.01310  -1.00
 Residual             0.0936648 0.30605

随时间变化的预测变量对发展趋势的影响

导入包与数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 导入包
library(haven)
library(psych)
library(lme4)

# 导入数据
setwd("/Users/nanxu/研究生课程作业/心理统计/课件数据/14第十四章 多层线性模型在追踪研究中的应用/")
data1 <- read_sav("./14-9.sav")
data2 <- read_sav("./14-10.sav")

# 查看数据
names(data1)
dim(data1)
names(data2)
dim(data2)

数据介绍与数据合并

1
2
3
4
5
6
7
8
9
10
# 描述数据
describe(data1)
describe(data2)

table(unique(data1$id) == data2$id)

# 合并数据
merged_data <- merge(data1, data2, by = "id")
names(merged_data)
dim(merged_data)
1
2
3
# 不考虑第二水平预测变量的解释作用，对于第一水平随时间变化的预测变量假设为固定参数
model <- lmer(marhap ~ marpro1 + ager_25 + (marpro1 | id) + (ager_25 | id), data = merged_data)
summary(model, standardized=TRUE)

固定部分参数估计结果

1
2
3
4
5
Fixed effects:
             Estimate Std. Error        df t value Pr(>|t|)    
(Intercept)  31.25034    0.27993 170.73475 111.636  < 2e-16 ***
marpro1      -2.26712    0.28439 408.28264  -7.972 1.58e-14 ***
ager_25      -0.13618    0.02197 225.26668  -6.199 2.69e-09 ***

从固定部分参数可以看出，婚姻幸福感marhap随着年龄ager_25增加有显著的下降趋势(β20\beta _{20}为-0.13618，Pr(>|t|)为2.69e-09),近期家庭中是否存在问题marpro1对婚姻幸福感marhap有显著的影响，有问题的个体比没有问题的个体平均低2.26712

随机部分参数估计结果

1
2
3
4
5
6
7
8
Random effects:
 Groups   Name        Variance Std.Dev. Corr
 id       (Intercept) 0.00000  0.0000       
          marpro1     3.77998  1.9442    NaN
 id.1     (Intercept) 0.96071  0.9802       
          ager_25     0.02832  0.1683   0.24
 Residual             5.95213  2.4397       
Number of obs: 910, groups:  id, 231